Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Агрегатный индекс физического объема.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если продукцию двух сравниваемых периодов оценить в одних и тех же неизменных ценах, то стоимость продукции двух сравниваемых периодов будет отличаться лишь за счет изменения объема продукции. Поэтому общий индекс, рассчитанный как отношение стоимости продукции двух периодов в одних и тех же ценах, называют агрегатным индексом физического объема:
Он характеризует отношение объема услуг отчетного периода в базисных ценах к фактическому объему услуг в денежном выражении базисного периода. В агрегатном индексе физического объема в качестве соизмерителя обычно принимаются цены базисного периода. Внешней отличительной особенностью любого агрегатного индекса является то, что и в числителе, и в знаменателе данного индекса имеется сумма произведений двух показателей, один из которых меняется, т.е. выступает в роли индексируемой величины, а второй остается неизменным, т.е. выступает в роли соизмерителя (весов). Разность между числителем и знаменателем индекса физического объема отражает прирост объема продукции в денежном выражении за счет увеличения количества (физического объема) отдельных видов продукции: DQ=Sq1p0 – Sq0p0.
При построении агрегатного индекса физического объема могут использоваться и другие соизмерители. Так, если принять в качестве соизмерителя с е б е с т о и м о с т ь единицы продукции в базисном периоде
Тогда разность между числителем и знаменателем
покажет как изменились общие издержки (затраты) на производство в связи с изменением выпуска продукции. Если в качестве соизмерителей принять з а т р а т ы в р е м е н и на единицу продукции в базисном периоде
а разность будет характеризовать изменение общих затрат времени на производство продукции за счет изменения объема выпуска.
Агрегатный индекс цен По аналогии с индексом физического объема для определенного набора товаров может быть построен и агрегатный индекс цен (индекс качественного показателя). При этом рассуждения остаются те же: если нельзя суммировать цены на различные товары, то можно суммировать и сопоставлять стоимости этих товаров. Однако, сопоставляя два значения стоимости Агрегатная формула общего индекса цен была впервые предложена в 1864г. немецким ученым Ласпейресом. Он предлагал строить агрегатный индекс цен, приняв в качестве весов продукцию базисного периода. Т.о. индекс цен Ласпейреса выглядит:
В 1874г. другой немецкий ученый Пааше, предложил строить агрегатный индекс цен по продукции текущего периода. Т.о. индекс цен Пааше выглядит:
На практике используются формулы индексов цен и Ласпейреса и Пааше, хотя они и дают разные результаты. (По значению индекс Ласпейреса, как правило, больше индекса Пааше). Каждый из этих индексов имеет свои особенности, которым отдается предпочтение в конкретных условиях использования. Так, индекс цен Ласпейсеса удобен для оперативной (недельной, месячной, квартальной) информации об изменении цен на определенный фиксированный набор товаров, когда пересчет каждый раз на текущее количество товаров сопряжен с большими затратами труда и времени. По формуле Ласпейреса рассчитывают индекс потребительских цен (ИПЦ). В то же время формуле Пааше отдается предпочтение, когда индекс цен рассматривается в системе с индексом стоимости и индексом физического объема. (Индекс стоимости услуг равен произведению индекса физического объема услуг и индекса цен).
Данную систему индексов можно построить и по индексу цен Ласпейреса, но как правило, строится система индексов с использованием индекса цен Пааше, т.к. данная система лучше интерпретируется.
Кроме того, при расчете индекса цен по формуле Пааше, вычитая из числителя знаменатель, легко определить в абсолютном выражении сумму доходов (или потерь) за счет изменения цен на продукцию отчетного периода.
Разность между числителем и знаменателем индекса цен Ласпейреса Sp1q0 – Sp0q0 характеризует не реальный, а условный эффект: каков был бы прирост стоимости продукции в результате изменения цен при базисном количестве продукции. Такие вопросы в практической деятельности редко возникают.
Формально все индексы можно разделить на две группы по использованию весов базисного периода (Ласпейреса) и отчетного периода (Пааше):
Между индексами Ласпейреса и Пааше существуют определенные взаимосвязи и соотношения – свойства, которые полезно применять на практике в индексных расчетах. Свойства индексов Ласпейреса и Пааше заключаются в следующем: 1. Индекс цен в формуле Пааше равен отношению индекса стоимости продукции к индексу физического объема в формуле Ласпейреса:
2.
В начале ХХ в. американский экономист Фишер предложил вместо формул индексов Ласпейреса и Пааше использовать среднюю геометрическую из них. Индексы Фишера представляет собой среднюю геометрическую из произведения двух агрегатных индексов Лайспейреса и Пааше:
Этот индекс Фишер назвал «идеальным», поскольку в нем не отдается предпочтение ни продукции базисного периода, ни продукции текущего периода. Однако индекс Фишера из-за его формальности и трудности экономической интерпретации используется редко, в основном при территориальных сопоставлениях. Экономический смысл геометрической формы индексов затруднен: разность между числителем и знаменателем не покажет никакой реальной экономии (потерь) из-за изменения цен и объемов продукции. Индекс-дефлятор определяется отношением фактической стоимости продукции отчетного периода к стоимости объема продукции отчетного года в ценах базисного года. В основе расчета индекса-дефлятора лежит формула Пааше:
Реальный ВВП рассчитываются в i-том году на основании номинального ВВП и индекса-дефлятора i-того года следующим образом: Ri = Di: Id, где Ri – реальный валовой внутренний продукт, измеряемый объемом товаров и услуг, произведенных в текущем году (q1) по ценам базисного года (p0); Di – номинальный ВВП, измеряемый объемом товаров и услуг, произведенных в текущем году (q1) в текущих ценах (p1).
По аналогии можно записать агрегатные индексы для некоторых других качественных показателей. Агрегатный индекс себестоимости продукции, рассчитанный по количеству продукции отчетного периода:
показывает, во сколько раз в среднем изменилась себестоимость продукции. Разница между числителем и знаменателем индекса, представляющая собой разность между фактическими затратами на производство продукции в текущем году и условными затратами на производство продукции текущего года, рассчитанными по себестоимости базисного периода, позволяет оценить реальную экономию затрат на производство продукции в результате снижения себестоимости продукции: Sq1c1 – Sq1c0.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1958; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.10 (0.007 с.) |

 .
.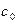 , то агрегатный индекс физического объема будет выглядеть следующим образом:
, то агрегатный индекс физического объема будет выглядеть следующим образом:

 , то формула агрегатного индекса физического объема будет иметь вид:
, то формула агрегатного индекса физического объема будет иметь вид:

 , мы должны показать изменение последней только за счет изменения цен, т.е. необходимо устранить влияние изменения количества производимой в разные периоды продукции на стоимостной показатель
, мы должны показать изменение последней только за счет изменения цен, т.е. необходимо устранить влияние изменения количества производимой в разные периоды продукции на стоимостной показатель 
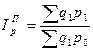

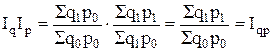 .
.




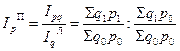 .
.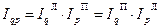 .
. ;
; 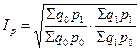 .
. .
.