
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряды индексов с постоянными и переменными весамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Два и более индексов с одинаковыми по содержанию и во времени весами образуют ряд индексов с постоянным весами или соизмерителями: Iq = Два и более индексов с одинаковыми по содержанию, но различными во времени весами или соизмерителями называются рядом индексов с переменными весами или соизмерителями: Iq = В статистической практике ежегодные индексы объема промышленной продукции вычисляются как индексы с постоянными соизмерителями или весами, т.к. продукция оценивается в сопоставимых ценах. Ежегодные индексы физического объема продукции в торговле вычисляются как индексы с переменными весами или соизмерителями.
9.6. Взаимосвязи индексов. Индексный метод выявления роли отдельных факторов динамики сложных явлений Многие статистические показатели, характеризующие различные стороны общественных явлений, находятся между собой в определенной связи (часто в виде произведения). Связь между экономическими показателями находит свое отражение и во взаимосвязи характеризующих их индексов. В общем случае, если z = yx, то Iz = IyIx, а если z = y/x, то и Iz = Iy / Ix.. Поэтому многие, связанные между собой экономические показатели, образуют индексные системы. Система взаимосвязанных индексов дает возможность применять индексный метод для изучения взаимосвязи общественных явлений, проведения факторного анализа с целью определения роли отдельных факторов (не зависимых друг от друга) на изменение сложного явления В отечественной статистике практике принята следующая практика факторного анализа. Если результативный показатель можно представить как произведение объемного и качественного показателя, то, определяя влияние объемного фактора на изменение результативного показателя, качественный фактор фиксируют на уровне базисного периода. Если же определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода. Рассмотрим построение взаимосвязанных индексов на примере индексов цен, физического объема продукции (если речь идет об отпускных ценах промышленности) или физического объема товарооборота (если речь идет о розничных ценах) и индекса стоимости (товарооборота в фактических ценах). Индексы физического объема и цен являются факторными по отношению к индексу стоимости продукции (товарооборота в фактических ценах):
Таким образом произведение нидекса цен наиндекс физического объема продукции дает индекс стоимости продукции (товароооборота в фактических ценах), то есть индексы образуют индексную систему из трех индексов. Если, например, по определенной группе товаров цена единицы товара в отчетном периоде по сравнению с базисным возросла в среднем на 20% (Ip,= 1,20), а физический объем товарооборота в фиксированных ценах снизился на 5% (Iq = 0,95), то можно определить изменение объема товарооборота в фактических ценах: Ipq = Ip . Iq = 1,20 . 0,95 = 1,14 или 114%. Таким образом, при снижении физического объема товарооборота на 5%, товарооборот в фактических ценах в отчетном периоде по сравнению с базисным вырос на 14% вследствие роста цен на единицу товара в среднем на 20%. Аналогично можно найти взаимосвязь между индексами затрат на производство продукции, себестоимости и физического объема продукции: Izq = Iz . Iq Индекс изменения общего фонда оплаты труда в связи с изменением общей численности работающих Т и заработной платы f: IF = IT . If К числу взаимосвязанных индексов относятся и индексы переменного состава, индексы постоянного состава и индексы структурных сдвигов. В этой системе динамика среднего показателя (индекса переменного состава) выступает как произведение двух индексов: индекса среднего показателя в неизменной структуре (индекс постоянного состава) и индекса влияния изменения структуры явлений на динамику среднего показателя (индекс структурных сдвигов):
Индексная система позволяет определить влияние отдельных факторов на формирование уровня результативного показателя, по двум известным значениям индексов найти значение третьего – неизвестное. Например, известно, что затраты на производство всей продукции в отчетном периоде по сравнению с базисным выросли на 15% (Izq = 1,15) и одновременно уровень себестоимости единицы продукции снизился на 4% (Iz = 0,96), то можно определить, что физический объем продукции вырос на 20%:
Рассмотренные системы являются двухфакторными (результативный признак связан с двумя факторами). Но общий признак может зависеть от трех. Четырех и более факторов, то есть связь может трех-, четырехфакторная и т.д.
Поэтому общие индексы могут быть разложены также на три, четыре и более факторных индекса, объясняющих изменение результативного признака за счет влияния каждого фактора в отдельности. Обозначим факторные признаки a, b, c, тогда система взаимосвязанных индексов будет иметь следующий вид:
Аналогично строится система взаимосвязанных индексов при четырехфакторной связи и т.д. Аналогично строится система взаимосвязанных индексов при большем количестве факторов - четырех и т.д.
Контрольные вопросы к теме «Индексный метод» 1. Что понимается под индексом в статистике? 2. Какие задачи решаются с помощью индексов? 3. На какие виды подразделяются индексы по степени охвата элементов исследуемой совокупности? 4. Что собой представляют индивидуальные индексы и изменение каких элементов совокупности они характеризуют? 5. Можно ли утверждать, что индивидуальные индексы по методам исчисления адекватны коэффициентам (темпам) роста? 6. Какова сущность общих (сводных) индексов, что они характеризуют? 7. Каковы особенности расчета агрегатных индексов? 8. В чем заключается проблема выбора весов или соизмерителей при построении агрегатных индексов? 9. Как в общих (сводных) индексах определяется величина абсолютного изменения тех или иных показателей? 10. Как рассчитываются агрегатные индексы цен Пааше и Ласпейресса и чем можно объяснить различия получаемых результатов? 11. В чем заключается эффект Гершенкрона, применительно к индексам Пааше и Ласпейреса? 12. Как исчисляется «идеальный» индекс цен Фишера и что он отражает? 13. Когда возникает необходимость преобразования агрегатного индекса в средний арифметический и средний гармонический? 14. При соблюдении, каких условий средний арифметический и средний гармонический индексы тождественны агрегатному? 15. Как исчисляются цепные и базисные индексы? 16. Какая существует взаимосвязь между цепными и базисными индексами и когда она проявляется в индивидуальных и общих (сводных) индексах? 17. Что представляют собой индексы с постоянными и переменными весами? 18. Что характеризуют и как исчисляются индексы переменного, постоянного (фиксированного) состава и структурных сдвигов? 19. Какая существует взаимосвязь между индексами переменного, фиксированного состава и структурных сдвигов? 20. Какова роль индекса структурных сдвигов в исследовании динамики средних показателей и воздействие какого фактора и как можно определить с его помощью? 21. Что представляет собой система взаимосвязанных индексов и для чего она применяется? Приведите примеры взаимосвязи индексов. 22. Можно ли, используя формулы взаимосвязи индексов, оценить влияние различных факторов на изменение сложного явления?
Контрольные задания по теме «Индексный метод» 1. Цены и продажа продуктов на центральном рынке города представлены следующими данными:
Определите: 1. Индивидуальные индексы цен (по каждому виду товаров). 2. Индивидуальные индексы физического объема реализации товаров.
3. Общий индекс цен: а) Ласпейреса; б) Пааше; в) Фишера. 4. Общий индекс физического объема. 5. Общий индекс товарооборота (стоимости товаров). 6. Покажите взаимосвязь между исчисленными индексами. Сделайте выводы.
2. Имеются следующие данные о продаже акций:
Определите: 1. Общий индекс цен на акции компаний. 2. Общий индекс количества акций. 3. Общий индекс стоимости всех акций. Сделайте выводы. 3. Объем произведенной продукции и ее себестоимость характеризуются следующими данными:
1. Рассчитать общий (сводный) индекс себестоимости продукции. 2. Определить изменение общих затрат на производство (относительное и абсолютное) и разложить абсолютный прирост (уменьшение) по факторам: а) за счет изменения себестоимости единицы продукции отдельных б) за счет изменения количества произведенной продукции.
4. Имеются следующие данные о затратах труда на единицу продукции и объемах ее производства:
Определите: 1. Общий индекс трудоемкости единицы продукции. 2. Общий индекс производительности труда. Покажите взаимосвязь исчисленных индексов. Сделайте выводы. 5. Имеются следующие данные о реализации фруктов:
Вычислите: 1. Индивидуальные индексы физического объема продукции. 2. Общие индексы физического объема товарооборота в сопоставимых ценах и товарооборота в фактических ценах. 3. Общий индекс цен на основании взаимосвязи индексов.
6. Имеются следующие данные о реализации продукции на одном из рынков города:
Определите общие индексы: 1. товарооборота; 2. физического объема товарооборота; 3. цен и сумму экономии (или перерасхода) денежных средств от изменения цен. Сделайте выводы.
6. Имеются следующие данные о товарообороте базисного периода и индивидуальных индексах:
1. Вычислите общие индексы: товарооборота в фактических ценах, цен и физического объема товарооборота. Рассчитывая эти индексы, не используйте взаимосвязь между ними. Используйте эту взаимосвязь только для проверки полученных результатов. 2. Определите абсолютное изменение товарооборота, вызванное изменением цен. Проанализируйте полученные данные.
8. По цеху мужской одежды швейного объединения имеются следующие данные о затратах на производство изделий и изменении их себестоимости:
Требуется рассчитать: 1. Индивидуальные индексы себестоимости. 2. Общие индексы себестоимости и затрат на производство (издержек производства). 3. Индекс физического объема производства на основании взаимосвязи индексов. 4. Сумму экономии (перерасхода) общих затрат, полученную в результате изменения себестоимости. Сделайте выводы.
10. Имеются следующие данные о выпуске однородной продукции по предприятиям АО:
Определите по трем предприятиям: 1. Общие индексы себестоимости переменного, постоянного состава и структурных сдвигов. 2. Абсолютный прирост (снижение) средней себестоимости и структуры произведенной продукции. Сделайте выводы. 11. От двух предприятий, производящих продукт «А», получены следующие данные:
1. Рассчитать индексы производительности труда: а) переменного состава;
б) фиксированного состава; в) индекс влияния структурных сдвигов на динамику средней 2. Определить абсолютный прирост продукта «А» и разложить его по а) за счет изменения производительности труда; б) за счет изменения общей численности рабочих; в) за счет изменения структуры занятых на производстве рабочих.
12. По одному из отделений Сбербанка города имеются следующие данные о вкладах населения:
Определить: 1. Средний размер вклада для всего населения в базисном и отчетном периодах. 2. Индексы среднего размера вклада переменного, фиксированного состава и структурных сдвигов. 3. Абсолютный прирост суммы вкладов всего, в том числе, за счет изменения числа вкладов, изменения среднего размера вклада и сдвигов в структуре вкладов по видам. Сделайте выводы.
13. По рынку города имеются следующие данные о продаже продуктов:
Определить: 1. Цепные и базисные индивидуальные индексы цен и количества проданных фруктов. 2. Цепные и базисные общие индексы цен и физического объема товарооборота с постоянными и переменными весами. Показать взаимосвязь между цепными и базисными индексами.
14. Имеются данные об изменении потребительских цен в одном из регионов РФ за период 2004-2007 г.г.:
Определить изменение потребительских цен за весь период.
15. Базисный индекс общего объема продукции легкой промышленности края (в сопоставимых ценах) за период 2001-2007 г.г. равен 1,30. Цепной индекс за 2008 год равен 1,047. Определите базисный индекс общего объема продукции легкой промышленности за период 2001-2008 г.г. 16. Цепные индексы объёма продукции пищевой промышленности области (в сопоставимых ценах) составили: в 2005г. – 1,048, в 2006г. – 1,049; в 2007г. – 1,031; в 2008г. – 0,98. Определить базисный индекс физического объёма продукции пищевой промышленности. 17. Базисный индекс общего объёма продукции машиностроения области за период 1999 – 2008гг. равен 154,2%. В 2007г. по сравнению с 1998г. объём этой продукции возрос на 45%. Определить цепной индекс, характеризующий изменение общего объёма продукции машиностроения в 2008г. по сравнению с 2007 годом.
[1] См.: Россия 2007: Стат. справочник/ Росстат. – М., 2007. – С. 8. [2] См.: Россия 2007: Стат. справочник/ Росстат. – М., 2007. – С. 4.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.147.141 (0.012 с.) |

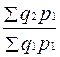 ; Iq =
; Iq = 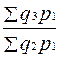 ; Iq =
; Iq = 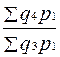
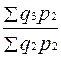 ; Iq =
; Iq = 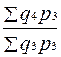
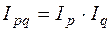 или
или 
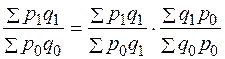
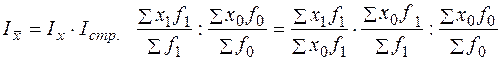
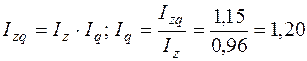 или 120%.
или 120%.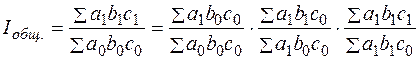
 190,0
190,0



