
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Информация о вкладах в банке для расчета средних значенийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В октябре известен средний размер вкладов каждого вида х и количество вкладов f. Следовательно, для расчета среднего размера вклада по двум видам применяем формулу средней арифметической взвешенной, тыс. руб.:
В ноябре известен средний размер вкладов каждого вида, а количество вкладов не известно, но зато имеются данные об общих суммах вкладов. Путем деления сумм вкладов М каждого вида на их средний размер вклада х можно определить веса – число вкладов по их видам f, а затем определить средний размер вклада по двум видам по формуле средней арифметической. Однако, если в расчете использовать среднюю гармоническую, то отпадает необходимость предварительного расчета весов – размеров вкладов по каждому виду, поскольку эта операция заложена в саму формулу. Средняя гармоническая взвешенная применяется, когда статистическая информация не содержит частот f по отдельным единицам совокупности, а представлена как произведение xf. Чтобы исчислить среднюю, обозначим xf =М, откуда f=w/x. Преобразуем формулу средней арифметической так, чтобы по имеющимся данным x и М можно было исчислить среднюю. В формулу средней арифметической взвешенной вместо xf подставим М, вместо f – отношение М/x и получим формулу средней гармонической взвешенной:
Итак, средний размер вклада в ноябре по двум их видам находим по формуле средней гармонической взвешенной, тыс. руб.:
Пример 5. В результате проверки двух партий муки потребителям установлено, что в первой партии муки высшего сорта было 3942 кг., что составляет 70,4% общего веса муки этой партии. Во второй партии муки высшего сорта было 6520 кг., что составляет 78,6% общего веса муки этой партии. Определите процент муки высшего сорта в среднем по первой и второй партиям вместе. Решение Средний процент муки высшего сорта по двум партиям определяем по формуле средней гармонической взвешенной:
Средняя геометрическая
Пример 1. Предположим, Вы внесли деньги в банк на срочный депозит, процент по которому ежегодно изменяется в зависимости от ставки рефинансирования ЦБ. После каждого года сумма, равная процентному приросту, добавляется к сумме счета. Например, первоначальная сумма вклада составила 100 денежных единиц. За первый Вы получили 5% дохода по вкладу, за второй 7%, за третий 9% и за 4-й – 10%. Каков средний уровень дохода по вкладу за 4 года?
Можно сложить вычислить среднюю арифметическую величину дохода: Ведем следующие условные обозначения: P – первоначальная сумма вклада, Если первоначальная сумма вклада - Р, то после первого года она возрастает и становится Если необходимо определить средний процент дохода i, который даст сумму дохода F по истечении четырех лет, при прибавлении ежегодного накопленного прироста к сумме вклада, то это будет величина, которая определится из следующего уравнения:
Решение этого уравнения находится по формуле:
где (i+1) - геометрическая средняя из (1+i1),(1+i2),(1+i3),(1+i4)). Средний процент дохода по вкладу равен Общий вид формулы средней геометрической невзвешенной:
Средней геометрической взвешенной:
Согласно правилу мажорантности средней, расчет по средней арифметической завышает результат, чем длиннее период расчета, тем больше будет ошибка.
Пример 2. В результате инфляции за первый год цена товара возросла в два раза к предыдущему году, а за второй год еще в три раза к уровню предыдущего года. Ясно, что за два года цена возросла в 6 раз. Каков средний темп роста цены за год? Арифметическая средняя здесь непригодна, поскольку, если за год цена выросла бы в (2+3)/2=2,5 раза, то за два года цена выросла бы в 2,5 *2,5 = 6,25, а не в 6 раз. Геометрическая средняя даст правильный ответ:
Геометрическая средняя дает наиболее правильный по содержанию результат осреднения, если задача состоит в нахождении такого значения признака, который качественно был бы равно удален как от максимального, так и от минимального значения признака.
Пример 3. Максимальный выигрыш в лотерее составляет миллион рублей, а минимальный – сто рублей. Какую величину можно считать средней между миллионом и сотней? Арифметическая средняя явно непригодна, так как составляет 500050 рублей, а это, как и миллион, крупный, а никак не средний выигрыш. Геометрическая средняя в этом случае дает наиболее правильный с точки зрения экономики и логики ответ:
Контрольные вопросы по теме «Средние показатели» 1. Каковы условия необходимости применения и типичности средней величины? 2. Какая величина должна быть использована в качестве обобщающей средней характеристики, чтобы число отклонений индивидуальных значений признака от нее было минимальным? 3. Какой показатель обладает свойством: алгебраическая сумма отклонений индивидуальных значений признака от него равна 0? 4. Если все значения признака ряда уменьшить в одно и тоже число раз, то что произойдет со средней арифметической? 5. Чем обусловливается выбор способа вычисления средней величины? 6. В чем заключается правило мажорантности средних? 7. Средняя арифметическая, мода и медиана как меры центральной тенденции.
Контрольные задания по теме «Средние показатели» 1. Общий размер капитала пяти коммерческих банков составлял 18,8 млн. ден. ед., а общая сумма прибыли – 51,7 млн. ден. ед. Определить среднюю прибыльность капитала.
2. Просроченнаязадолженность по кредитам акционерным обществ (АО) за отчетным период характеризуется следующими данными:
Определить средний процент просроченной задолженности акционерного общества.
3. Доходы банков в отчетном году характеризуется следующими показателями:
Определить среднюю процентную ставку. 4. Результаты работы страховых организаций в Ι полугодии характеризуется следующими данными:
Определить: 1) средний коэффициент выплат; 2) абсолютную сумму дохода страховых операций; 3) относительную доходность.
5. Продукция, производимая малым предприятием, имеет разный уровень рентабельности реализации. В декабре этот показатель составил:
Определите средний уровень рентабельности реализации продукции. Обоснуйте выбор средней.
6. В будние дни на протяжении торговой недели цена изделия оставалась на уровне 246 руб. «Распродажная» цена в субботу и в воскресенье была ниже на 20%. Определить среднюю цену изделия за неделю.
7. Фондовый индекс в течение пяти лет изменился со следующими годовыми темпами прироста: +10%, +20%, +15%, -30%, +20%. Определить среднегодовой темп прироста за пять лет.
8. Первые два года фирма увеличивала выручку от реализации на 10% или в 1,1 раза ежегодно, за следующие три года она увеличивала выручку ежегодно на 20% или в 1,2 раза. Чему равен среднегодовой темп роста выручки от реализации за весь период работы фирмы?
9. За первый год производительность труда выросла на 10%, за второй упала на 5%, а за третий выросла на 4%. Чему равен среднегодовой прирост производительности труда?
10. На сколько процентов ежегодно должна снижаться себестоимость единицы продукции, чтобы за пять лет произошло ее снижение на 30%?
11. Автомобиль совершил рейс общей протяженностью 500 км, из которых 240 км прошла со скоростью 100 км в час, 160 км – со скоростью 90 км в час и 100 км – со скоростью120 км в час. Вычислите среднюю скорость с которой машина прошла весь путь.
12. Имеются данные о финансовых показателях фирм, тыс. руб.:
Определите средний процент рентабельности акционерного капитала фирм, используя показатели: а) гр.1 и 2; б) гр. 2 и 3; в) гр. 1 и 3; г) гр. 3 и 4.
13. Имеются следующие данные об оплате труда работников малых предприятий:
Определите среднюю заработную плату работников предприятий, используя показатели: а) гр. 1 и 2; б) гр. 2 и 3; в) гр. 1 и 3; г) гр. 3 и 4. 14. Банк имеет данные о работе трех обменных пунктов валюты за день:
Определите средний взвешенный курс доллара по трем обменным пунктам банка, используя показатели: а) гр. 1 и 2; б) гр. 1 и 3; в) гр. 2 и 3. Тема 6. Показатели вариации
В социально-экономическом анализе важно знать не только среднее (или серединное) значение признака, но на сколько равномерно распределены эти значения относительно среднего значения. Поясним сказанное. Пусть заданы два вариационных ряда. Ряд I: 1, 2, 3, 4, 5, 6, 6, 7, 8, 9, 10, 11 Ряд II: 4, 5, 5, 5,6, 6, 6, 6, 7, 7, 7, 8 Рассчитаем для этих рядов среднюю арифметическую, моду и медиану. Ряд I. Ряд II. Оба ряда имеют одинаковое число наблюдений n=12 и имеют одинаковые значения средней арифметической, медианы и моды - все равные 6. Но мы ясно видим, что ряды различны. В чем же состоит суть различий между ними?
Рисунок 1 графически изображает ряд I и ряд II. Оба ряда имеют одинаковые среднюю арифметическую, моду и медиану. Однако значения признака в первом ряду более широко разбросаны: они лежат дальше от средней по сравнению со вторым рядом, то есть вариация признака в первом ряду значительнее, чем во втором. Ряд I более вариабелен, чем ряд II. В статистике используется ряд мер вариабельности (колеблемости). Наиболее простые из них: Интерквартильный размах – разница между первым и третьим квартилями. Чем больше величина интерквартильного размаха, тем больше рассеяние признака. Интерквартильный размах в ряду I равен 5.5, интерквартильный размах в ряду II равен 2. Размах вариации - разность между наибольшим и наименьшим значениями признака. Записывается: Существуют и другие более тонкие и чаще используемые меры вариации, которые, подобно средней, арифметической используют всю информацию, содержащуюся в вариационном ряду. Мы можем определить вариацию как меру отклонений значений признаков вариационного ряда от центра ряда распределения - средней арифметической. Например, можно взять сумму отклонений значений каждого признака ряда от средней арифметической:
где n – число признаков ряда. Однако, сумма отклонений всех вариантов от их средней арифметической, согласно свойству средней арифметической, всегда равна нулю. Для нахождения меры вариации можно каждое отклонение от средней взять по абсолютному значению. Эта операция изменяет отрицательные знаки отклонений на положительные, и мера вариации в этом случае не равна нулю.
Для взвешенных вариант:
Другой способ избежать нулевой суммы при исчислении средней суммы отклонений индивидуальных значений признака от среднего арифметического – возвести в квадрат каждую разность:
Для взвешенных вариант:
Дисперсия вариационного ряда есть средняя арифметическая квадрата отклонения (средний квадрат отклонения) значений признаков ряда от их средней арифметической. (Поскольку s - греческая буква, то дисперсию часто просто называют сигма-квадрат, а заглавная греческая буква сигма S используется нами как символ, обозначающий суммирование) Определим теперь стандартное отклонение (среднее квадратическое отклонение): Стандартное отклонение вариационного ряда есть арифметическое значение корня квадратного из дисперсии. __ s = Ös2 Для чего мы используем стандартное отклонение, если уже имеем такую меру вариации признаков как дисперсия? Желательно, чтобы показатель рассеяния выражался в тех же единицах измерения, что и значение признака (дисперсия этим свойством не обладает). Извлекая квадратный корень из дисперсии, мы получаем показатель, имеющий ту же единицу измерения, что и анализируемый признак. В чем смысл дисперсии и среднего квадратического отклонения? Как мы можем интерпретировать их значения? По определению s2 - средний квадрат отклонений вариантов от средней арифметической, это - мера рассеяния всех значений вариантов относительно средней арифметической. Чем больше вариация, тем дальше от средней находятся возможные значения признаков. Если сравнивают два вариационных ряда, то тот из них, который имеет большую дисперсию и среднее квадратическое отклонение, более вариабелен. Риск, ассоциируемый с инвестициями, часто измеряют стандартным отклонением возврата инвестиций. Если сравниваются два типа инвестиций с одинаковой ожидаемой средней возврата, то инвестиции с более высоким средним квадратическим отклонением считаются более рискованными (хотя более высокое стандартное отклонение предполагает возврат более вариабельный с обеих сторон - как ниже, так и выше средней). В научном анализе предпочтительно использование дисперсии, так как она имеет ряд полезных математических свойств, на практике же лучше работать со стандартным отклонением, поскольку эта мера легко интерпретируется. Для ручного счета лучше пользоваться формулой дисперсии следующего вида, которая легко выводится из формулы (2) __ _ s2 = х2 - (х)2
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1455; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.162.87 (0.016 с.) |





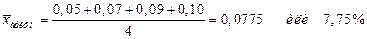 . Верно ли это?
. Верно ли это? - доход по вкладу в первый, второй, третий и четвертый годы соответственно (в долях единиц), F – сумма вклада по истечении четырех лет.
- доход по вкладу в первый, второй, третий и четвертый годы соответственно (в долях единиц), F – сумма вклада по истечении четырех лет. . В конце второго года эта сумма составит
. В конце второго года эта сумма составит  . В конце третьего года:
. В конце третьего года:  . По истечении четырех лет сумма составит
. По истечении четырех лет сумма составит 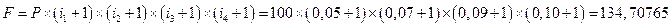

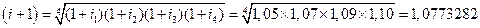 ,
, , что отличается от результата, полученного по средней арифметической.
, что отличается от результата, полученного по средней арифметической.
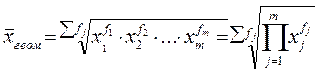 (5.4)
(5.4) раза.
раза. руб.
руб.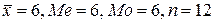 .
. Рис.1. Сравнение вариации рядов I и II
Рис.1. Сравнение вариации рядов I и II
 . Размах вариации в первом ряду равен 10. Размах вариации во втором ряду равен 4. Размах вариации и интерквартильный размах - меры разброса признаков в наборе данных. В первом ряду разброс выше, чем во втором. Недостаток этих мер в том, что размах вариации содержит информацию только о расстоянии между наибольшим и наименьшим значениями, а интерквартильный размах содержит информацию только о разности между верхним и нижним квартилями. Интерквартильный размах - более устойчив к значениям крайних вариантов.
. Размах вариации в первом ряду равен 10. Размах вариации во втором ряду равен 4. Размах вариации и интерквартильный размах - меры разброса признаков в наборе данных. В первом ряду разброс выше, чем во втором. Недостаток этих мер в том, что размах вариации содержит информацию только о расстоянии между наибольшим и наименьшим значениями, а интерквартильный размах содержит информацию только о разности между верхним и нижним квартилями. Интерквартильный размах - более устойчив к значениям крайних вариантов. ,
, - среднее линейное отклонение,
- среднее линейное отклонение,
 - дисперсия,
- дисперсия,



