Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели изменения уровней ряда динамикиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Большинство статистических характеристик ряда динамики основано на абсолютном или относительном сравнении его уровней. Сравниваемый уровень принято называть текущим, а уровень, с которым производится сравнение, - базисным. Показатели роста и прироста предназначены для характеристики изменения уровней ряда (yt). Показатели роста представляют собой отношение двух уровней ряда, а прироста - их разность. Если эти показатели имеют вид относительных величин, их называют коэффициентами. Если они выражены в процентах - темпами. Они могут быть цепными и базисными. У цепных ведется сравнение текущего уровня с предыдущим, а у базисных - с начальным, принятым за базу. В качестве базисного выбирается либо начальный уровень ряда, либо уровень, с которого начинается какой-то новый этап развития явления.
Пример 1. Рассчитать показатели роста и прироста для анализа динамики числа кредитных организаций
Таблица. Кредитные организации (на начало года)
2001 – базисный год.
Абсолютное изменение уровней ряда измеряется показателем абсолютного прироста. Цепные показатели прироста исчисляются так: D2ц = y2 - y1 D3ц = y3 - y2 D 4ц = y4 - y3 ... D iц = yi - yi-1
Базисные показатели прироста: D2б = y2 - y1 D3б = y3 - y1 D4б = y4 - y1 ... Diб = yi - y1
Абсолютный прирост характеризует увеличение или уменьшение уровней ряда за определенный промежуток времени. Абсолютные приросты с переменной базой (цепные) называют скоростью роста или первыми разностями. Цепные и базисные абсолютные приросты по данным примера 1 показывают сокращение (прирост) кредитных организаций и абсолютные изменения по сравнению с 2001 годом. Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, то есть общему приросту за весь промежуток времени. Для характеристики интенсивности, то есть относительного изменения уровней ряда динамики исчисляют коэффициенты или темпы роста (снижения). Цепные коэффициенты роста исчисляются следующим образом: К2/1ц = Цепные темпы роста будут иметь следующий вид: Т2/1ц=(K2/1ц)100%, T3/2ц= (K3/2ц)100%, ….
Базисные же коэффициенты будут такими:
К2/1б = Базисные темпы роста: T2/1б=(K2/1б)100%, T3/2б=(K3/2б)100% … Они показывают во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если коэффициент больше 1) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). (см. Пример 1) Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного коэффициента роста на предыдущий уровень равно соответствующему цепному коэффициенту роста. Относительную оценку скорости изменения уровня ряда в единицу времени дают показатели коэффициентов (темпов) прироста. Темп прироста показывает на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения. Он представляет собой отношение абсолютного прироста к предыдущему или начальному (базисному) уровню. Цепной темп прироста: Т пр.ц.=(D y ц/ y i-1)100% T пр.б.=(D y б/ y 1)100% Темп прироста можно получить и из темпа роста, если из него вычесть 100%. Коэффициент прироста получается вычитанием 1 из коэффициента роста. При анализе динамики развития следует так же знать какие абсолютные значения скрываются за темпами роста и прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени зачастую показывает, что при снижении темпов прироста абсолютный прирост не всегда уменьшается, в отдельных случаях он может возрастать. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением (содержанием) одного процента прироста и рассчитывают как отношение абсолютного прироста к темпу прироста за тот же период времени, %:
Абсолютное значение одного процента прироста показывает какое абсолютное значение скрывается за относительным показателем – одним процентом прироста (см. пример 1). В тех случаях, когда сравнение производится с отдалением периода времени, принятого за базу сравнения, рассчитывают, так называемые, пункты роста, которые представляют собой разность базисных темпов роста, %, двух смежных периодов. В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно суммировать, в результате получаем базисные темпы прироста. (см. пример 1). Средний темп (коэффициент) роста или прироста позволяет оценить среднюю скорость изменения уровней временного ряда. Средний коэффициент роста исчисляется с помощью средней геометрической простой или взвешенной. Взвешенная используется тогда, когда значения некоторых коэффициентов роста повторяются. Средняя геометрическая простая имеет следующую формулу:
где К1,К2,К3...Кn- цепные коэффициенты роста за n периодов. Поскольку произведение цепных коэффициентов дает базисный коэффициент роста, а базисный коэффициент можно получить делением конечного уровня на начальный, постольку приведенную выше формулу можно записать еще и так:
Если бы начальный уровень был обозначен через y0 , то корень надо было бы брать n-ой степени, а не степени n-1. Средний коэффициент роста для примера 1 составит
Следовательно, средний темп роста здесь составил 90,25%, а средний темп прироста равен –9,75%. Средний темп роста ни в коем случае нельзя исчислять по формуле средней арифметической. Согласно правилу мажорантности средних при использовании средней арифметической всегда получается завышенный результат по сравнению со средней геометрической. При коротких рядах это завышение может быть не очень заметным, но при длинных рядах оно может оказаться очень существенным. Средняя геометрическая взвешенная имеет такой вид:
Если два первых года ежегодный прирост был бы равен 20%, а последующие три года - 40%, то надо было бы воспользоваться последней формулой, которая в данном случае дала бы следующее значение среднегодового коэффициента роста
Последний расчет вполне допустимо записать еще и так:
В соответствии с этим средняя геометрическая может получить такой вид:
где Кi - цепной коэффициент роста в i-том периоде, wi - вес i-того периода, исчисляемый как:
Причем обязательно Smi =1. В статистике для сравнения базисных темпов роста изучаемых рядов динамики за анализируемый период принято исчислять коэффициент опережения Где
8.4. Приемы преобразования временных рядов Преобразование временных рядов включает в себя приемы, позволяющие сделать ряды более удобными для анализа. В частности, оно включает в себя такие приемы, как приведение рядов к одному основанию и смыкание рядов. Приведение рядов к одному основанию позволяет лучше увидеть, какой ряд растет быстрее, а какой медленнее. К этому приему приходится прибегать тогда, когда сравниваемые ряды имеют разные начальные периоды, исчислены в разной валюте или имеют другие различия, затрудняющие их непосредственное сравнение. Для приведения рядов к одному основанию выбирается один, общий для всех рядов начальный период, который берется за 100%. Надо сказать, что выбор начального периода в какой-то мере предопределяет результаты анализа: при одной начальной базе более “быстрым” может показаться один ряд, а при другой базе - иной. Приведем пример. Имеются следующие данные о численности населения Ростовской области за ряд лет: Численность населения Ростовской области (тыс.чел. на начало года)
Если взять за базу 1970 г., то можно будет сделать вывод о более быстром росте городского населения: Динамика численности населения Ростовской области в процентах к 1970 г.
Картина получится совсем иной, если взять за базу 1988 г. Для последнего случая мы будем иметь такую таблицу:
Динамика численности населения Ростовской области в процентах к 1988 г.
Данный пример говорит о том, что надо очень продумано подходить к выбору начальной базы для сравниваемых рядов. Выбор упомянутой базы - проблема не математическая, а общеэкономическая. Никакого простого правила для правильного выбора начальной базы рядов, приводимых к одному основанию, не существует. Надо только помнить, что выбор начальной базы может тем или иным способом повлиять на конечный вывод. Надо также понимать, что это обстоятельство может быть использовано недобросовестными исследователями для сознательного искажения динамики изучаемых явлений. Смыкание временных рядов. К этому приему приходится прибегать тогда, когда надо создать один длинный, сквозной ряд из нескольких коротких рядов, отличающихся либо методологией расчета показателей, либо границами территории, либо ценами, что не позволяет их соединить вместе без всяких пересчетов. Смыкание рядов может быть осуществлено только в том случае, если ряды имеют хотя бы один общий период. Для иллюстрации приведем следующий пример. По одному из районов области имеются данные о численности населения с 1970 г. по 1990 г. в одних границах, а с 1990 г. по 1998 г. - в других. Эти данные представлены ниже: Численность населения района на начало года (тыс.чел.)
Поскольку у двух рядов имеется один общий год, постольку их смыкание возможно. По данным этого общего года исчисляем коэффициент пересчета данных для старых границ в данные для новых границ:
С помощью этого коэффициента делаем пересчет численности населения: для 1970 г. 200х1.25 = 250 для 1985 г. 230х1.25 = 287.5 Можно сделать и обратный пересчет - из новых границ в старые: для 1995 г. 330: 1.25 = 264 для 2000 г. 340: 1.25 = 272 В результате этих пересчетов получаем такую таблицу: Численность населения района на начало года (тыс.чел.)
Контрольные вопросы к теме «Анализ динамики социально-экономических процессов»
1. Что такое ряды динамики и из роль в статистическом анализе? 2. Укажите виды рядов динамики. 3. Чем объясняется выбор формулы для нахождения среднего уровня динамического ряда? 4. Какие показатели рассчитываются для характеристики изменений уровней ряда динамики? 5. Как рассчитывается средний темп (коэффициент) роста и прироста? 6. В каких случаях применяют «период удвоения ряда»? 7. Укажите приемы, применяемые для преобразования временных рядов. 8. Каким образом временные ряды приводят к одному основанию? 9. Чем вызвана необходимость смыкания временных рядов? 10. Назовите методы анализа основной развития в рядах динамики. 11. На чем основан метод укрупнения интервалов? 12. Охарактеризуйте метод скользящей средней, его недостатки и достоинства. 13. Чем вызвана необходимость аналитического выравнивания рядов? 14. Какие уравнения регрессии наиболее часто используются для выравнивания динамических рядов? 15. Какой критерий применяется для оценки качества модели динамического ряда? 16. Как измеряются сезонные колебания в динамических рядах? 17. Как рассчитываются индексы сезонности? 18. Как измеряется автокорреляция в рядах динамики? 19. Дайте понятие экстраполяции рядов динамики. 20. Укажите простейшие приемы прогнозирования.
Контрольные задания к теме «Анализ динамики социально-экономических процессов»
1. Имеются следующие данные об остатках сырья и материалов на складе предприятия, млн. руб.: на 1/01 – 400; на 1/02 - 455; на 1/03 – 465; на 1/04 – 460. Определить среднемесячный остаток сырья и материалов на складе предприятия за 1 квартал. 2. Имеются следующие данные об остатках дебиторской задолженности фирмы “Сатурн” на начало месяца (тыс. руб.):
Определите: 1)вид ряда динамики; 2) среднемесячные уровни остатка дебиторской задолженности за I, за II кварталы и за полугодие; 3) изменение остатка дебиторской задолженности во II квартале по сравнению с I кварталом. 3. Остатки вкладов населения в сбербанках города в 2002 году характеризуются следующими данными на 1-е число месяца, руб.:
Определите: среднемесячные остатки вкладов за 1 и 2 кварталы; средние остатки вкладов за полугодие; абсолютный прирост изменения среднего остатка вклада во II квартале по сравнению с I. 4. Имеются следующие данные о товарных запасах розничного торгового предприятия, млн. руб.: на 1.01.2002 г. – 61,1; на 1.05.2002 г. – 57,5; на 1.08.2002 г. – 51,3; на 1.01.2003г. – 74,7. Вычислить среднегодовой товарный запас розничного торгового предприятия за 2002 год. 5. Остаток средств на расчетном счете предприятия составил на 1.01.2003 г. 180 тыс. руб., 15.01 поступило на расчетный счет 900 тыс. руб., 22.01. списано со счета 530 тыс. руб., 27.01 поступило 380 тыс. руб. С 28.01. до конца месяца остаток средств на расчетном счете не изменился. Определить среднесуточный остаток средств на расчетном счете предприятия в январе. 6. Определить, на сколько рублей и на сколько процентов различаются средние остатки по вкладам за I квартал, если на 1.01.2003 г. остаток по первому вкладу составлял 500 у.е., по второму вкладу – 700 у.е. В течение I квартала имели место следующие изменения величины остатков вкладов (у.е.):
Определить среднегодовое производство продукции за 1993 – 1998 гг. 7. Имеются следующие данные Госкомстата РФ о количестве россиян отдыхающих за рубежом в период 1999-2003 годы (тыс. чел.):
Для анализа ряда динамики исчислите: - абсолютные приросты, темпы роста, темпы прироста – базисные и цепные, абсолютное содержание 1% прироста, пункты роста. Полученные данные представьте в таблице; - среднегодовое количество россиян, отдыхающих за рубежом; - среднегодовой абсолютный прирост; - среднегодовые темпы роста и прироста; - изобразите динамику россиян, отдыхающих за рубежом, на графике. Сделайте выводы. 8. Ввод в действие жилых домов предприятиями всех форм собственности в одном из регионов в 1997-2001 годах характеризуется следующими данными, млн. кв. м общей площади:
Для анализа ряда динамики исчислите: - абсолютные приросты, темпы роста, темпы прироста – базисные и цепные, абсолютное содержание 1% прироста, пункты роста. Полученные данные представьте в таблице; - средний уровень ряда; - среднегодовой абсолютный прирост; - среднегодовые темпы роста и прироста 9. Производство продукции предприятия характеризуется следующими данными:
Проведите анализ ряда динамики и исчислите: - абсолютные приросты, темпы роста, темпы прироста – базисные и цепные, - абсолютное содержание 1% прироста, пункты роста. Полученные данные представьте в таблице; - средний уровень ряда; - среднегодовой абсолютный прирост; - среднегодовой темп роста и прироста. 10. Имеются следующие данные о производстве продукции предприятия за 1998-2003 гг. (в сопоставимых ценах), млн. руб.
Определить аналитические показатели ряда динамики производства продукции предприятия за 1998-2003 гг. - абсолютные приросты, темпы роста, темпы прироста – базисные и цепные, - абсолютное содержание 1% прироста, пункты роста. Полученные данные представьте в таблице; - средний уровень ряда; - среднегодовой абсолютный прирост; - среднегодовой темп роста и прироста. 11. Имеются следующие данные о продаже легковых автомобилей в РФ:
Для анализа ряда динамики исчислите: - абсолютные приросты, темпы роста, темпы прироста – базисные и цепные, - абсолютное содержание 1% прироста, пункты роста. Полученные данные представьте в таблице; - средний уровень ряда; - среднегодовой абсолютный прирост; - среднегодовой темп роста и прироста. 12. Имеются данные о бюджетных расходах РФ на исследования и разработки в постоянных ценах 1996 г. за 1996 – 2004 гг.
Рассчитайте показатели динамики затрат на исследования и разработки за период 1996 – 2004 гг. Сделайте выводы.
13. Количество дорожно-транспортных происшествий (ДТП), совершенных водителями в регионе, увеличилось в 1995 по сравнению с 1990 годом на 2 тыс. или на 4%; в 2000 году по сравнению с 1995 годом их число возросло на 30%, а в 2002 году по сравнению с 2000 годом – на 2%. Определить количество ДТП в 1990, 1995, 2000 и 2002 годах. 14. Численность населения региона возросла за период с 1.01.1999 по 1.01.2002 г. на 4,2%, при этом удельный вес мужского населения за этот период увеличился с 42,1 до 44,3%. Определить показатели динамики численности мужского и женского населения региона. 15. Удельный вес городского населения региона увеличился с 1.01 1993 г. по 1.01.2000 г. с 36,2 до 42,8%. Определить показатели динамики численности городского и сельского населения региона, если общая численность населения данного региона за этот период возросла на 8,4%. 16. Динамика объема реализации услуг коммунальных предприятий города в процентах к 1999г. составила: 2000г. – 108,0; 2001 г. – 110,5; 2002 г. – 125,0; 2003 г. – 153,2. Определить среднегодовой темп прироста за период 1999 – 2003 гг. 17. Среднегодовые темпы роста продукции за период 1999 – 2003 гг. в тяжелой промышленности составили 102,6%, а в легкой промышленности – 105,3%. Величина продукции в 2003 г. (в у.е.) составила в тяжелой промышленности – 7820, а в легкой – 8590. Определите среднегодовой темп роста продукции в целом за период 1999 – 2003 гг. 18. Заполнить таблицу:
19. Имеются данные о среднемесячной заработной плате на одного работника и стоимости набора 25 основных продуктов питания в расчете на одного человека в РФ за первое полугодие 1999 года.
Привести ряды динамики к сопоставимому виду, вычислить коэффициенты опережения, сделать краткие выводы. 20. Имеются данные о динамике кредитов коммерческих банков по видам (по состоянию на 1 января), млн. руб.:
Приведите ряды к одному основанию. Определите коэффициенты опережения темпов роста краткосрочных кредитов по сравнению с долгосрочными кредитами. 21. Имеются следующие данные о розничном товарообороте по одному из районов города (млн. руб.). Осуществить смыкание рядов.
22. Приведите уровни следующего ряда динамики, характеризующие численность работников фирмы, к сопоставимому виду, чел.:
23. Имеются данные об объеме продукции (млн. руб.), вычисленные по старой и новой методике. Приведите уровни ряда к сопоставимому виду.
Тема 9. Индексный метод
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2056; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.016 с.) |

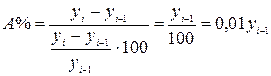
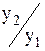 К3/2ц =
К3/2ц = 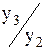 К4/3ц =
К4/3ц = 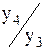 ... Кi/i-1ц =
... Кi/i-1ц = 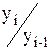
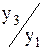 К4/1б =
К4/1б = 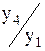 ... Кi/1б =
... Кi/1б = 
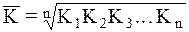 ,
,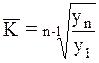 .
. 0,9025
0,9025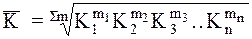 .
.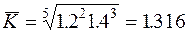
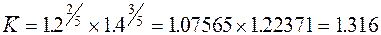 .
.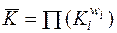 ,
,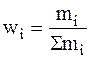 .
.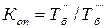 ,
,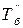 - базисный темп первого ряда;
- базисный темп первого ряда;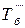 - базисный темп второго ряда.
- базисный темп второго ряда.