Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды и формы средних величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:
Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:
Числитель исходного соотношения средней представляет собой определяющий показатель. Для средней заработной платы таким определяющим показателем является фонд заработной платы. Независимо от того, какой первичной информацией мы располагаем - известен ли нам общий фонд заработной платы или заработная плата и численность работников, занятых на отдельных должностях, или какие-либо другие исходные данные - в любом случае среднюю заработную плату можно получить только через данное исходное соотношение средней. Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней. Если, например, требуется рассчитать средний размер вклада в банке, то исходное соотношение будет следующим:
Если же необходимо определить среднюю процентную ставку по кредитам, выданным на один и тот же срок, то потребуется следующее исходное соотношение:
Однако от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины: · средняя арифметическая; · средняя гармоническая; · средняя геометрическая; · средняя квадратическая, кубическая и т.д. Перечисленные средние объединяются в общей формуле средней степенной (при различной величине k): Общая формула степенной средней записывается следующим образом:
При k = -1, получим среднюю гармоническую величину:
При k = 0 получим среднюю геометрическую (Вывод формулы в учебнике ОТС Ефимова М.Р. стр. 94-95)
При k = 1 получим среднюю арифметическую:
При k = 2 – среднюю квадратическую
Поскольку вариационные ряды обычно сгруппированы по одинаковым значениям признака, либо в интервалах его значений, то чаще для расчетов применяют формулы средних взвешенных. В этих формулах в качестве весов выступают значения частот. Взвешенные формулы имеют вид:
Во всех формулах xi –индивидуальные значения признака; fi – частота повторения индивидуального значения признака, n – объем совокупности. Степенные средние, исчисленные для одной и той же совокупности, имеют различные количественные значения. Это отражено в правиле мажорантности средних.
Помимо степенных средних в экономической практике также используются средние структурные, среди которых наиболее распространены мода и медиана. При осреднении уровней динамических рядов применяются различные виды средней хронологической. Средняя арифметическая Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной. Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным. Предположим, восемь предприятий фирмы имеют следующий объем выпуска за месяц:
Для того, чтобы определить средний месячный выпуск в расчете на одно предприятие, можно воспользоваться следующим исходным соотношением:
Используя приведенные в предыдущем параграфе условные обозначения, запишем формулу данной средней:
С учетом имеющихся данных получим:
В данном случае мы использовали формулу средней арифметической простой (невзвешенной). Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными. Рассмотрим следующий условный пример: Сделки по акциям эмитента "Х" за торговую сессию
Определим по данному дискретному вариационному ряду средний курс продажи 1 акции, что можно сделать, только используя следующее исходное соотношение:
Чтобы получить общую сумму сделок необходимо по каждой сделке курс продажи умножить на количество проданных акций и полученные произведения сложить. В конечном итоге мы будем иметь следующий результат:
Расчет среднего курса продажи произведен по формуле средней арифметической взвешенной:
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Так, в приведенном выше примере количество проданных в ходе каждой сделки акций соответственно составляет 37,8% (0,378); 10,8% (0,108) и 51,4% (0,514) от их общего числа. Тогда, с учетом несложного преобразования формулы (5.4.) получим:
или
На практике наиболее часто встречаемая при расчете средних ошибка заключается в игнорировании весов в тех случаях, когда эти веса в действительности необходимы. Предположим, имеются следующие данные: Себестоимость продукции "Z"
Можно ли по имеющимся данным определить среднюю себестоимость данной продукции по двум предприятиям, вместе взятым? Можно, но только в том случае, когда объемы производства данной продукции на двух предприятиях совпадают. Тогда средняя себестоимость составит 38,0 руб. (доказательство этого правила будет приведено ниже.). Однако на первом предприятии за рассматриваемый период может быть произведено, к примеру, 50 единиц продукции, а на втором - 700 единиц. Тогда для расчета средней себестоимости потребуется уже средняя арифметическая взвешенная:
Общий вывод заключается в следующем: использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство. При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений от интервалов переходят к их серединам. Рассмотрим следующий пример:
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1034; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

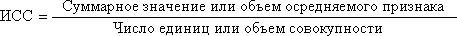

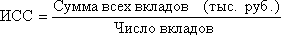

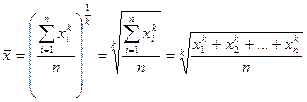
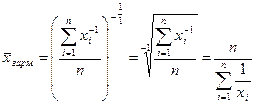
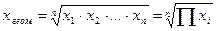
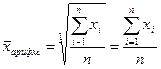
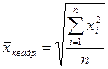
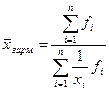


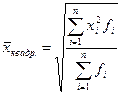


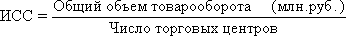
 (5.1)
(5.1)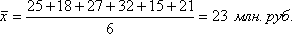

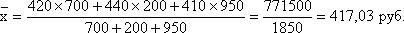
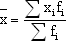 (5.2)
(5.2) (5.3)
(5.3)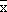 = 420 · 0,378 + 440 · 0,108 + 410 · 0,514 = 417,03 руб.
= 420 · 0,378 + 440 · 0,108 + 410 · 0,514 = 417,03 руб.