
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Истинное значение измеряемой величиныСодержание книги
Поиск на нашем сайте
Приведенные выше данные показывают, что, строго говоря, измерения абсолютно точно истинного значения любой величины невозможно в принципе. Поэтому более корректный способ представления результата любого измерения состоит в том, что экспериментатор указывает свою наилучшую оценку измеряемой величины, а также интервал, в котором, как он уверен, она лежит. Таким образом, задача экспериментатора состоит в том, чтобы уменьшить влияние погрешностей за счет правильной техники измерений, сделать правильную наилучшую оценку результата измерения и величины погрешности этого результата. Рассмотрим случай, когда систематические ошибки отсутствуют, а имеют место лишь случайные погрешности. Предположим, что нами произведено n измерений некоторой величины х, при этом получены n значений этой величины х1 х2 хi….хn. Округлим эти величины с учетом приборной ошибки и расположим в порядке возрастания. Определим в полученном множестве значений количество повторов (выпадений) отдельных результатов - ∆ni и вычислим вероятности их выпадения по формуле:
Полученные результаты также внесем в таблицу и построим на их основе график (рис.1) зависимости вероятности повторов отдельных результатов измерения от их величины - хi, т.е. функцию
хв.
Рис. 1.
Из полученного рис.1 видно, что наиболее вероятным является некоторый результат хi= хв, которому соответствует максимальное значение вероятности выпадения Pmax. Если этот результат (хв) принять за истинный, то абсолютную ошибку каждого измерения ∆хi, можно найти из выражения: ∆хi= хi- хв и более того истинный результат измерения, очевидно, должен удовлетворять условию:
∆хi= хi- хв=0 (7)
В этом можно убедиться, рассчитав абсолютные ошибки всех измерений, числа повторов каждой ошибки ∆n0 и вероятности выпадения ошибок Затем построим зависимость вероятности выпадения результатов измерений P от (хi-z) для трех значений z (z<xв, z=xв, z>xв). На рисунке 2 представлена эта зависимость, которая представляет собой туже зависимость P, что на рис.1. (и получена из тех же результатов), но сдвинутая на величину z влево по оси абсцисс. Ясно, что P имеет максимум при z=xв в нуле, а при других значениях z максимум отличается от нуля.
Тогда, если рассмотреть функцию
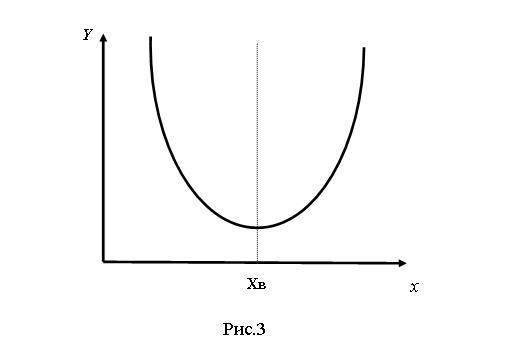
где xi – результат i-го измерения, n – число измерений, то о её свойствах можно сказать следующее. Функция y(x) всегда положительна, так как является суммой квадратов. Она имеет минимум при x=xв, что следует из данных представленных на рис.2. Качественно функция y(x) изображена на рисунке 3.
Известно, что для нахождения экстремума функции необходимо приравнять нулю ее производную. Возьмем производную от функции (4) и приравняем её нулю.
Тогда получаем:
Таким образом, истинное значение наиболее близко находится к наиболее вероятному значению xв, которое равно среднему арифметическому
Обработка результатов прямого измерения
Учитывая вышеизложенное, можно рекомендовать следующий алгоритм обработки результатов прямых измерений. 1. Из-за наличия погрешностей никогда не следует ограничиваться одиночным измерением, а всегда следует проводить несколько опытов желательно нечетное число (три, пять). 2. Определить наилучшее значение измеряемой величины х, как среднее арифметическое из всех результатов измерений: х1, х2... хi... хn по формуле:
3. Вычислить случайную абсолютную ошибку каждого измерения по уравнению (3):
а затем среднюю абсолютную погрешность:
4. Определить приборную погрешность, используя паспортные данные прибора или, при их отсутствии, принять за погрешность половину наименьшего деления шкалы стрелочного прибора или наименьший разряд цифрового прибора. 5. Сравнить приборную и среднюю абсолютную погрешность, выбрать большую из них, приняв за полную погрешность результаты измерения. Окончательный результат можно представить в виде:
Отработка результатов косвенных измерений Метод частных производных Пусть интересующая нас величина y является некоторой функцией других величин xl, x2, x3 и т.д., так что
у = ƒ(xl, x2, x3...) (13)
причем величины xl, x2, x3... мы можем измерять путем прямых измерений. В этом случае мы для определения величин
Для определения полной абсолютной погрешности величины у необходимо выяснить, как изменяется эта величина при относительно небольших изменениях всех величин, от которых зависит величина у. Это можно сделать с помощью полного дифференциала. Интересующее нас изменение величины
где От бесконечно малых изменений величин dу, dxl, dx2, dx3... в (15) перейдем к конечным значениям их изменений (погрешностям) ∆у, ∆xl, ∆x2, ∆x3...
где ∆y - искомая полная погрешность величины Под частной производной функции ƒ(x, y, z) по переменной X понимают величину:
т.е. это производная, которая вычисляется в предположении, что все переменные, кроме той, по которой берется производная, являются постоянными величинами. Например: пусть
После вычисления абсолютной ошибки ∆у по формуле (16) находят относительную ошибку как
Этот способ удобен в том случае, когда
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 (6)
(6) .
. Pmax
Pmax хi
хi

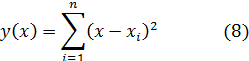

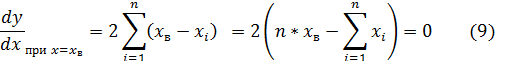
 (10)
(10) , получаемое от нескольких идентичных измерений.
, получаемое от нескольких идентичных измерений. (11)
(11)
 ,
, (12)
(12) Это означает, что истинное значение лежит в интервале
Это означает, что истинное значение лежит в интервале  .
.
 , а также полные погрешности, в определении этих величин, которые обозначим как
, а также полные погрешности, в определении этих величин, которые обозначим как  Наилучшее (среднее) значение косвенно определяемой величины у находится при подстановке в (13) наилучших (средних) значений
Наилучшее (среднее) значение косвенно определяемой величины у находится при подстановке в (13) наилучших (средних) значений

 (15)
(15) - обозначают частные производные от функции f по соответствующим переменным. Эти частные производные вычисляются при наилучших (средних) значениях
- обозначают частные производные от функции f по соответствующим переменным. Эти частные производные вычисляются при наилучших (средних) значениях  (16)
(16) - значения соответствующих частных производных, вычисленных при наилучших (средних) значениях входящих в них величин; ∆xl, ∆x2, ∆x3... - полные погрешности определения соответствующих величин. Также необходимо в (16) заменить знаки '-' между слагаемыми на знаки '+', поскольку формула (16) является оценкой абсолютной погрешности по максимуму (по наихудшему случаю, когда все ошибки складываются).
- значения соответствующих частных производных, вычисленных при наилучших (средних) значениях входящих в них величин; ∆xl, ∆x2, ∆x3... - полные погрешности определения соответствующих величин. Также необходимо в (16) заменить знаки '-' между слагаемыми на знаки '+', поскольку формула (16) является оценкой абсолютной погрешности по максимуму (по наихудшему случаю, когда все ошибки складываются). (17)
(17) . Тогда
. Тогда


 (17)
(17) представляет собой алгебраическую сумму.
представляет собой алгебраическую сумму.


