Ошибка репрезентативности, методика вычисления ошибки средней и относительной величины.

В статистике выделяют два основных метода исследования - сплошной и выборочный. При проведении выборочного исследования обязательным является соблюдение следующих требований: репрезентативность выборочной совокупности и достаточное число единиц наблюдений. При выборе единиц наблюдения возможны ошибки смещения, т.е. такие события, появление которых не может быть точно предсказуемым. Эти ошибки являются объектив­ными и закономерными. При определении степени точности выборочно­го исследования оценивается величина ошибки, которая может прои­зойти в процессе выборки - случайная ошибка репрезентативности (m) -является фактической разностью между средними или относительными величинами, полученными при проведении выборочного исследования и аналогичными величинами, которые были бы получены при проведении исследования на гене­ральной совокупности.

Оценка достоверности результатов исследования предусматривает определение:

1. ошибки репрезентативности

2. доверительных границ средних (или относительных) величин в генеральной совокупности

3. достоверности разности средних (или относительных) величин (по критерию t)

Расчет ошибки репрезентативности (m_м) средней арифмети­ческой величины (М):

, где σ - среднее квадратическое отклонение; n - численность выборки (>30).

Расчет ошибки репрезентативности (m_Р) относительной величины (Р):

, где Р - соответствующая относительная величина (рассчитанная, например, в %);

q =100 - Ρ% - величина, обратная Р; n - численность выборки (n>30)

В клинических и экспериментальных работах довольно часто приходится использовать малую выборку, когда число наблюдений меньше или равно 30. При малой выборке для расчета ошибок репрезентатив­ности, как средних, так и относительных величин, число наблюде­ний уменьшается на единицу, т.е.

; .

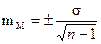Величина ошибки репрезентативности зависит от объема выборки: чем больше число наблюдений, тем меньше ошибка. Для оценки достоверности выборочного показателя принят следующий подход: показатель (или средняя величина) должен в 3 раза превышать свою ошибку, в этом случае он считается достоверным.

Знание величины ошибки недостаточно для того, чтобы быть уве­ренным в результатах выборочного исследования, так как конкрет­ная ошибка выборочного исследования может быть значительно больше (или меньше) величины средней ошибки репрезентативности. Для оп­ределения точности, с которой исследователь желает получить ре­зультат, в статистике используется такое понятие, как вероят­ность безошибочного прогноза, которая является характеристикой надежности результатов выборочных медико-биологических статистических исследований. Обычно, при проведении медико-биологических статистических исследований используют вероятность безошибочного прогноза 95% или 99%. В наиболее ответственных случаях, когда необходимо сделать особенно важные выводы в теоретическом или практическом отношении, используют вероятность безошибочного прогноза 99,7%

Определенной степени вероятности безошибочного прогноза соот­ветствует определенная величина предельной ошибки случайной выборки (Δ - дельта), которая определяется по формуле:

Δ=t * m, где t - доверительный коэффициент, который при большой выборке при вероятности безо­шибочного прогноза 95% равен 2,6; при вероятности безоши­бочного прогноза 99% - 3,0; при вероятности безошибочно­го прогноза 99,7% - 3,3, а при малой выборке определяется по специальной таблице значений t Стьюдента.

Используя предельную ошибку выборки (Δ), можно определить до­верительные границы, в которых с определенной вероятностью безо­шибочного прогноза заключено действительное значение статистичес­кой величины, характеризующей всю генеральную совокупность (сред­ней или относительной).

Для определения доверительных границ используются следующие формулы:

1) для средних величин:

,где Мген - доверительные границы средней величины в генеральной со­вокупности;

Мвыб- средняя величина, полученная при проведении исследова­ния на выборочной совокупности; t - доверительный коэффициент, значение которого определяет­ся степенью вероятности безошибочного прогноза, с кото­рой исследователь желает получить результат; m_M - ошибка репрезентативности средней величины.

2) для относительных величин:

, где Рген - доверительные границы относительной величины в гене­ральной совокупности; Рвыб- относительная величина, полученная при проведении иссле­дования на выборочной совокупности; t - доверительный коэффициент; m_P - ошибка репрезентативности относительной величины.

Доверительные границы показывают, в каких пределах может колебаться размер выборочного показателя в зависимости от причин случайного характера.

При малом числе наблюдений (n<30), для вычисления довери­тельных границ значение коэффициента t находят по специальной таблице Стьюдента. Значения t расположены в таблице на пересечении с избранной вероятностью безошибочного прогноза и строки, указывающей на имеющееся число степеней свободы (n), которое равно n-1.