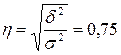Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Качественная оценка связи между признакамиСодержание книги
Поиск на нашем сайте
Пример. Рассчитать дисперсию, коэффициент детерминации и эмпирическое корреляционное отношение по данным таблицы.
Группировка населения отдельных областей России по среднему размеру ежемесячных денежных льгот пенсионеров
Сначала найдем средний размер льгот по трем областям в целом:
Вариация льгот по отдельным областям, обусловленная различием в местах проживания пенсионеров, характеризуется межгрупповой дисперсией:
Средняя из групповых дисперсий дает обобщающую характеристику случайной вариации, обусловленную отдельными факторами, кроме места проживания пенсионеров (например, характером занятости, стажем работы и т.п.):
Вариация льгот в изучаемых областях России, обусловленная влиянием всех факторов, вместе взятых, определяется общей дисперсией:
отсюда
Полученный коэффициент детерминации показывает, что дисперсия льгот зависит от места проживания пенсионеров на 32,5 %. Остальные 67,5% определяются множеством других неучтенных факторов.
Полученное значение эмпирического корреляционного отношения позволяет утверждать, что существует заметная связь между местом проживания пенсионеров и размером льгот. Пример. Большая торговая компания заказала опрос, цель – выяснение влияния фактора повышения квалификации на результаты работы агентов по продажам. Опрос 8 торговых агентов дал следующие результаты:
Среднее число контрактов, заключенных агентами:
В данном примере переподготовка – факторный признак, а число заключаемых контрактов – результативный. Сгруппируем эти данные по признаку переобучения и рассчитаем средние по каждой группе.
где n1 – число признаков в первой группе. Или по формуле для взвешенных вариант
где fi – частоты ряда.
где n2 – число признаков во второй группе. Рассчитаем дисперсию в каждой группе. Дисперсия числа заключенных контрактов у агентов, прошедших переобучение:
Дисперсия числа заключенных контрактов у агентов, не прошедших переобучение:
Рассчитаем среднюю из внутригрупповых дисперсий:
Этот показатель характеризует влияние на результативный признак всех прочих факторных признаков за исключением признака, положенного в основу группировки. Очевидно, что различие в числе заключенных контрактов в двух группах вызвано тем, что брокеры первой группы прошли переобучение, а брокеры второй группы не прошли. Найдем дисперсию между группами (межгрупповую дисперсию). Согласно формуле:
Общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
Проверим верность правила сложения дисперсий. Рассчитаем общую дисперсию числа заключенных контрактов
s2 = 8/8 = 1,00 В самом деле, 1,00 = 0,5625 + 0,4375. По данным примера эмпирическое корреляционное отношение равно:
Следовательно, фактор, положенный в основу группировки, существенно влияет на число заключаемых агентами контрактов, но существуют и другие факторы, влияние которых тоже заметно.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.219 (0.01 с.) |










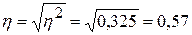
 .
. ,
, ,
, ,
,





 Этот показатель характеризует влияние на результативный признак факторного признака, положенного в основу группировки.
Этот показатель характеризует влияние на результативный признак факторного признака, положенного в основу группировки.