
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Индив и общие индексы.Принц постор системы взаимосв агрег индексов.Содержание книги
Поиск на нашем сайте
В зависимости от охвата индеек-мых явл:индив,общ,групповые. Инд индексы характер изменение отдел ед-ц статист совокупности(ip=p1/p0) Общие –выраж сводные или обобщающие рез-ты совместн изменения всех единиц,образ=их изучаемую совокупность.Могут рассчит в агрег и сред формах. Сущность ангег индекса сост в том,что несоизмеримые Эл-ты инд-го набора приводятся к соизмеримому виду путем их взвешивания на соизмерители-веса и дальнейшего суммирования по всем Эл-там индеек набора.Веса соизм ноб для перех от натур измерит разнородных ед-ц стат совок к однорон. Агрег индекс цены: Индекс физ объема Индекс стоим объема пр-ции При сравнивании числ и знам формул в разности опред абсол измен стоим пр-ции как в целом ьак и за счет изучаемых факторв.(формылы) М/д агрег индеек сущест та жде взаим что и м/д показателями:zq=z*q след Izq=Iz*
45. Средние индексы и их виды Общие индексы могут быть представл пкутем вычисления сред величин из индив индексов.Знач-я общ индексов,котые расчит по агрег способы и по способу средней будут одинаковы.iq=q1/q0 Так обр сред индеек могут быть представл как сред ариф или сред гарм из индив индексов.
46. Индекс метод нализа динамики среднего уровня Индексы дин сред ур-ня рассчит по различн качест показ.Индекс переменного состава Индекс пост сост,отраж измен сред цены в рез-те изменении индив цен на п/п при условии постоянства стр-ры
Индекс стр сдвигов,отраж изменении сред цены в рез-те измен стр-ры пр-ва пр-ции
47. Ряды индексов с пост и переменной базами сравнения,с пост и переем весами,их взаимосвязь При изучении динамики хоз деят приходяится производить идекное сопоставление более чем за 2 периода При этом инд величины могут определяться как на посто так и на переем базах сравнения.При исчислении базисн индексов получают хар-ки изменения изучаемых явлений во всех послед периодах по сравнению с начальным.Цепные индексы харакктериз послед измен изуч-го явлен из периода в период.Баз и цепн инд аналогичны относит величинам динамики. М/д инд цепн и базис индекс сущест взаимосвязь:произведен последовательных цепных индив индексов равна базисн инд-су точно такого же периода.
Цепные агрег Инде физ объема продукции с постоянными весами
Базис агрег с пост весами:
Взаимосвязь:
48.Взаимосвязи индексов Взаимосвязь:
(и все ранее)
49. Принципы построения многофакт индексов Агрег индекс можно использ для оценки влияния 2 факторов,кот-е формируют этот пока-ль,однако,индекс метод позвол определить влияние не только 2 но и большего числа факторов.При этом стат показатель котый явл рез-том изменения других,св-ых с ним показателей наз. Результативным,а показатели от кот-го завис результативный-факторным.Индекс метод аналит примен в тех случ когда м/д экон результативными и факторными показателями сущест функцион связь в частности когда результативность можно представить как произведение 2 или более факторных определяющих его величину. Принцип посторения 2-ух факторно модели:результатив пок-ли можно предствить как произв 2 фактор(кач и кол-во) P=k*vДельта р=з1-р0(оно происх под влиянием измен кач-ва дельта р(к)=(к1-к0)-v1 и за счет измен кол-ва дел р=(v1-v0)k0 Территориальные индексы В стат практике часто возник потребность в сопоставл уровни эк явл в простр-ве:по странам,н-н,обл.,т.е в исчислении террит индексов. Если стоит задача сравн цены 2 регионов то можно постр инд-сы: :
Разница м/д числит и знамент отобр сумму экон эф от различия цен. (написать формулы) Согласно методу станд весов можно рассчит индекст,в котором в качестве весов испол суммар V пр-ции по 2 регионам:
51 .Измерение связей м/ж соц-эк явл –важн задача статки.Формы и видвы взаимосв В процессе статистического исследования зависимостей вскрываются причинно-следственные отношения между явлениями, что позволяет выявлять факторы (признаки) оказывающие существенное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отношения – это связь явлений и процессов, когда изменение одного из них – причины – ведет к изменению другого – следствия. Cтатистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и от поставленных задач. С вязи между признаками и явлениями, ввиду их большого разнообразия, классифицируются по ряду оснований.
Признаки по их значению для изучения взаимосвязи делятся на два класса: 1)признаки, обуславливающие изменение других, связанных с ними признаков, называются факторными, или просто факторами; 2)признаки, изменяющиеся под действием факторных признаков, называются результативными. Связи между явлениями и их признаками классифицируются по степени тесноты связи, направлению и аналитическому выражению. В статистике различают функциональную связь, при которой определенному значению факторного признак соответствует одно и только одно значение результативного признак; и стохастическую связь, при которой причинная зависимость проявляется не в каждом отдельном случае, а в общем, среднем при большом числе наблюдений. Частным случаем стохастической связи является корреляционная связь. По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значений факторного признака происходит увеличение или уменьшение результативного (н-р, рост производительности труда способствует увеличению уровня рентабельности производства). В случае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака (например, с увеличением уровня фондоотдачи снижается себестоимость единицы произведенной продукции). По аналитическому выражению выделяют связи прямолинейные(линейные) и нелинейные (криволинейные). Если статистическая связь между явлениями может приближенно выражена уравнением прямой линии, то ее называют линейной связью; если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы и др.), то такую связь называют нелинейной. 52 Стат метод изуч связей Метод приведения параллельных рядовПриводится ряд данных по одному признаку и параллельно с ним – подругому признаку, связь с которым предполагается. По вариации признака впервом и втором ряду судят о наличии связи признаков. Такой метод позволяетвывести только направление связи, но не измерить ее.Балансовый методВзаимосвязь может быть также охарактеризована с помощью балансов.Графический метод Может использоваться как самостоятельно, так и совместно с другимиметодами.Если конкретные данные перенести на график, то полученное изображениеназывается полем корреляции. На оси абсцисс откладывается значениефакторного признака, а на оси ординат – результативного. Каждая единица,обладающая определенным значением факторного и результативного признака,обозначается точкой.Беспорядочное расположение говорит об отсутствии связи. Наоборот, чемсильнее связь, тем теснее точки группируются вокруг определенной линии.Метод аналитической группировки Сначала выбираются два признака: факторный и результативный. Полфакторному признаку производится группировка, а по результативному –подсчет средних или относительных величин.Путем сопоставления характера изменений значений факторного ирезультативного признака можно сделать вывод о наличии связи и еенаправлении. При помощи метода аналитической группировки можно сделатьвывод и о тесноте связи.53. Понятие линейной корреляции.Нахождение параметров уравнения регрессии,линейный коэффмциент корреляции
Для выявления наличия связи, ее характера и направления используются методы приведения параллельных данных, аналитических группировок, графический, корреляции и регрессии. Метод проведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Данное сопоставление позоляет установить наличие связи и получить представление о ее характере. Графический метод Графическая взаимосвязь двух признаков изображается с помощью поля корреляции. Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. Виды зависимостей: 1) парная корреляция – связь между двумя признаками (между двумя факторными либо между факторным и результативным признаком) 2) частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков 3) множественная корреляция – зависимость результативного и двух и более факторных признаков. Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками. Теснота связи количественно выражается величиной коэффициентов корреляции. Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции:
Линейный коэффициент корреляции изменяется в пределах от -1 до+1. По степени тесноты связи различают количественные критерии оценки тесноты связи:
Теснота связи при криволинейной зависимости измеряется с помощью корреляционного отношения. Различают эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение: Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины обусловлено влиянием одной или нескольких независимых величин (факторов). По форме зависимости различают: - линейную регрессию, которая выражается уравнением прямой (линейной функции) вида: - нелинейную регрессию, которая выражается уравнениями вида: парабола - гипербола - По направлению связи различают:
А) прямую регрессию (положительную), возникающую при условии, если с увеличением или уменьшением независимой величины значения зависимой также соответственно увеличиваются или уменьшаются; Б) обратную (отрицательную) регрессию, появляющуюся при условии, что с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.61.88 (0.011 с.) |





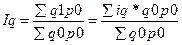 Cред гарм формула общего индекса цены:ip=p1/p0
Cред гарм формула общего индекса цены:ip=p1/p0 
 Этот индекс отраж измен как сред признака так и стр-ры совок.На его основе могут быть пост два других:
Этот индекс отраж измен как сред признака так и стр-ры совок.На его основе могут быть пост два других:
 С помощью данных инд можно рассчит абсол измен средних цен(разница).
С помощью данных инд можно рассчит абсол измен средних цен(разница).

 Цепн агр с перем весам
Цепн агр с перем весам Баз с переменными
Баз с переменными
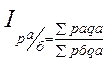

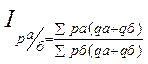


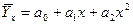
 и т.д.
и т.д.


