
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сред ариф,её осн мат св-ва и методы расчетаСодержание книги
Поиск на нашем сайте
Сред ариф вел- такое сред значен признака,при вычислении которого общих объем признак сов-сти сохр неизменным. Сред арифм прост: Если частоты выражены относит величинами(частостями w),то расчет средней также будет по арифм взвешенной: X=сумма XiW1/сумма Wi Основные матем св-ва сред арифм: 1)если варианты умен или увел на некотор пост число,то среднее соответственно умен или увел на это постоянное число. 2)если варианты или * или / на некоторое постоянное число,то среднее соотв увел или умен в это число раз 3)если частоты / или * на постоян число,то величина сред не измен 4)нулевое св-во средних(алгебр сумма отклонения вариант от средней равна 0) 5)x+-y(cреднее)=х(среднее)+-у(среднее) 6)х=с, то х среднее=с
25. Сред гармон и другие виды сред.Обусловленность выбора средней характером исходной информации В статистике используют различные виды средних величин. Выбоа средней зависит как от поставленной задачи,кот. правильно может разрешить только определ-ая ср-яя,так и от х-ра и содерж-я исходного мат-ла,имеющегося в конкр. случае. При расчете средних необх-мо исходить из экон-го содерж-я стат. показ-лей.В основе такого подхода лежит исходное соотношение ср-ей,т.е. соотн-е двух взаимосвяз-ых показ-ей,на осн-е кот. выбирается форма средней,а именно ср-ий уровень признака(Ср.ур.приз=отношение итога знач-ий призн-ка по сов-сти явлений к числу единиц сов-сти)Уяснив экон-кую природу ср.величины,необ-мо,чтобы все операции ее вычисления имели реал. смысл с точки зрения исходного соотн-я средней.При этом следует принимать во вним. опред-щее св-во сов-сти,когда общая колич. Х-ка ее не изменяется при замене индив-ых знач-ий приз-ка их ср-ей. 1)сред гарм прос Сред гарм взв 2)средне геом прост Сред геом взв Квадр взв
26. Мода и медиана,их смысл и значение,спосбы вычис . В экон. пратктике возникают ситуации, при кот. необходимо найти такое значение приз-ка, кот. имеет место в ряду. Если варианты ряда распред-я ранжированы в виде дискретного ряда, то структ-ые средние определяются визуально. Если имеем интерв-ый ряд с интерв-ами = по виличине, то сначала находим модальный или медиальный интервал,т.е. интер., обладающий наибольшей частотой, а затем определяют знач-е структ-ых средних по ф-лам. Наиболее распр-ые виды стр-ых средних:мода,медиана.Если ряд строится из чет-го числа членов, то медианой счит-ся ср.арифм-ая из 2х видов знач-ий.
Мода -ведичина признака, т.е. варианта,кот. встреч-ся в ряду чаще всего.Mo=XMo +i Xm0– нижн-я граница модаль-го интервала, i-величина интервала(ширина),fm;fm-1;fm+1-частоты предследств-го и след-го за модой интер-лов. Медиана -знач-е ряда,распол-го в его середине,т.е. такое знач-е,кот делит этот ряд по численности на 2 равные части Me=XMe+ i Мода и медиана-это конкретные велич,совпадающие с конкр-ми вариантами ряда.При построенииряда распред-я по количестьву его членов наиболее точной ср.величиной при анализе служит медиана.Если распр-е величин в ряду нормально, то мода, медиана и ср.арифм. по величине совпадают. Если распред-е симметр-но,то соотнош-ия этих 3х величин используют при анализе как хар-ку асимметрии .
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 317; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.46.174 (0.009 с.) |

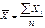 и взвеш.
и взвеш. 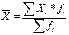
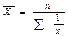
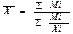
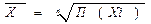
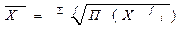 3)квадрат прост
3)квадрат прост 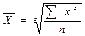
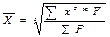
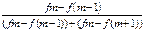
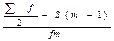 ,где Xm-ниж-я граница медиан-о интервала,Sm-1-сумма накоп-ых частот в интер-лах,предшест-их медиан-му.
,где Xm-ниж-я граница медиан-о интервала,Sm-1-сумма накоп-ых частот в интер-лах,предшест-их медиан-му.


