
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие кривол завис ,оценка тесноты связи при кривол зависимСодержание книги
Поиск на нашем сайте Корреляцию называют нелинейной, если график регрессии y = f(x) или x =?(yизображается кривой линией. На практике чаще всего (ис-ходя из удобства вычислений) рассматривают следующие функции рег-рессии: y = ax2 + bx + c – параболическая зависимость 2-го порядка, y = ax3 + bx2 + cx + d – параболическая зависимость 3-го порядка, y = a/x + b – гиперболическая зависимость. Неизвестные параметры, входящие в каждое из уравнений, нахо-дят методом наименьших квадратов, который приводит к системе урав-нений линейных относительно неизвестных коэффициентов. Для негруппированных данных при параболической зависимости 2-го порядка имеем систему уравнений Корреляционное отношение обладает свойствами: 1.???? 1; 2. При? = 0 признак Y с признаком Х корреляционной зависимостью не связан; 3. При? = 1признак Y связан с признаком Х функциональной зависимо-стью; 4. С ростом корреляционного отношения? от 0 до 1 связь между Yи Х становится более тесной, приближаясь к функциональной; 5.???r?; 6. При? =?r? имеет место точная линейная корреляционная зависи-мость. Замечания: 1. Корреляционное отношение служит мерой тесноты связи любой, в том числе и линейной зависимости (выборочный коэффициент корреля-ции r оценивает тесноту лишь линейной зависимости). 2. При нахождении регрессии Х на Y теснота связи определяется по формуле
55Понятие о множест коррел При изучении корреляционной зависимости между более чем двумя случайными величинами Х 1, Х 2,..., Хn с заданным совместным распределением используют множественные и частные коэффициенты корреляции и корреляционные отношения. Применение обычных коэффициентов парной корреляции при множественной корреляции для изучения связи двух случайных величин может привести к неправильным выводам. Если коэффициент парнойкорреляции между двумя случайными величинами уменьшается или становится близким к нулю при других фиксированных случайных величинах, то можно сказать, что взаимозависимость этих случайных величин в значительной мере (или определяющим образом) имеет место благодаря третьим факторам. Если же при фиксации третьих факторов степень взаимозависимости двух случайных величин возрастает, то это означает, что факторы «маскировали» истинную взаимозависимость двух случайных величин. Частный коэффициент корреляции – это мера линейной зависимости между двумя случайными величинами из некоторой совокупности случайных величин Х1, Х2,..., Хk, когда исключено влияние остальных случайных величин. Частный коэффициент выражается через элементы корреляционной матрицы, составленной из коэффициентов парной корреляции. Множественный коэффициент корреляции служит мерой линейной зависимости между случайной величиной Х1 и некоторым другим набором случайных величин Х2,..., Хk. Множественный коэффициент корреляции определяется как обычный коэффициент парной корреляции между Х 1и Х*, где Х* – наилучшее линейное приближение Х1 случайными величинами Х 2,..., Хk, коэффициенты которого определяются из соотношения При k = 2 множественный коэффициент корреляции совпадает с обычным коэффициентом корреляции. Для вычисления множественного коэффициента корреляции можно использовать формулу Именно это выражение оправдывает назначение коэффициента множественной корреляции как показателя тесноты линейной связи. В самом деле, чем лучше приближается случайная величина Х 1 линейными комбинациями случайных величин Х 2,..., Хk, тем ближе модуль этого коэффициента к единице; чем хуже линейное приближение, тем этот коэффициент ближе к нулю. Регрессионная модель, как и всякая другая математическая модель, выражая основные свойства изучаемого экономического или другого явления или объекта, не в состоянии полностью воспроизвести его поведение. Но даже то, что исследователь наметил отразить, трудно сделать в условиях реальной ситуации. Например, при изучении влияния минеральных удобрений на урожайность по фактическим значениям урожайности конкретной сельскохозяйственной культуры и фактическим дозам внесения минеральных удобрений под эту культуру на единицу площади в рамках определенной совокупности сходных хозяйств может оказаться, что коэффициент регрессии по этому фактору незначим. А это при прямолинейной трактовке служит основанием для вывода: минеральные удобрения не влияют на урожайность. На самом деле это, конечно, совсем не так. Более тщательное изучение всех условий, формирующих результирующий показатель и значения факторов, поможет выяснить обстоятельства неправильного вывода. Так, может оказаться, что во всех этих хозяйствах внесение минеральных удобрений находится примерно на одинаковом уровне и практически не сказывается на вариабельности результирующего признака. Могут быть и другие особенности, например, с увеличением внесения удобрений на единицу площади в меньшей степени соблюдаются агротехнические условия внесения и т. п.
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


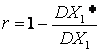 .
.


