
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды и способы отбора единиц в выбор сов-стьСодержание книги
Поиск на нашем сайте
При выборке существует несколько методов отбора ед-ц в выборочную совокупность. Различают повторный и бесповторный отбор; собственно случайную, механическую, серийную, комбинированную и малую выборки. В процессе проведения собственно случайной выборки включение единиц в выборочную совокупность может быть как повторным, так и бесповторным. При случайной повторной выборке соблюдается независимость способа отбора от изучаемых признаков и сохраняется равная возможность для каждой единицы совокупности быть включенной в выборку. При соблюдении этих условий возможно привлечение аппарата тер.вер. для оценки рез-в выборки. Случайная выборка позволяет получить объективную оценку генеральной совокупности. Она является отбором по жребию, т.к. единицы нумеруются, на каждую зав-ся жребий, которые перемешиваются, и на удачу отбираются. Собственно случайный отбор можно провести жеребъевкой при большой величине совокупности. Поэтому же признаку собственно случайный отбор проводится при помощи датчика случайных чисел. Если жеребъевка проводится по датчику случайных чисел, в выборку включают единицы с указанными номерами (например, каждая 10-я единица). Если же выборка бесповторная, отобранная единица обратно в совокупность не возвращается и вероятность оставшихся единиц попасть в выборку все время растет. Механический отбор – это отбор ед-ц, которые находятся на равном расстоянии друг от друга из какого-либо исходного перечня или расположения. При этом исходное расположение должно быть случайным, т.е. беспорядочным. Мех. отбор бывает повт. и бесповт. Выб. наблюдение может называться малой выборкой, когда выборочная сов-ть сос-т из небольшого числа ед-ц (не более 30). При рассмотре больших выборок сущ-т формы расчета ср. квадр. отклонения как суммы квадратов отклонений, деленных на число ед-ц. Стат-ка при выборочном наблюдении позволяет отобрать ед-цы, группы ед-ц и далее внутри группы исследовать либо все единицы, либо тоже производится выборка. Типичная выб-ка – вначале ген. сов-ть делят на группы по к-л признаку и внутри каж. группы проводится выборка. Серийная выборка – отбираются группы, т. е. серии, внутри кот. проводят сплошное наблюдение. Точность ее зависит только от величины дисперсий групповых средних. Бывает повторной и бесповторной. Серии м.б. равно- и неравновеликими.
Комбинированная выборка – предполагает использование нескольких способов выборки. Часто комбинируют серийную выборку и случайную с индивид. отбором единиц совокупности. В этом случае ген. совокупность делят на серии и,отбрав нужное число серий, производят случайную выборку единиц в сериях. Такая выб-ка бывает повторной и бесповторной. Одноступенчатая и многоступен. выб-ка. Если отобранные любым способом единицы подвергаются наблюдению, имеем одноступенчатый отбор. Многоступенчатая выборка- когда из ген. совокупности отбирают группы ед-ц, из этих групп – другие, меньшие по объему, и так до тех пор, пока не будут отобраны те группы или единицы, которые будут наблюдаться. Многофазная выборка – выборочная сов-ть образ. так, что одни сведения собираются у всех ед-ц, потом отбир. еще некоторые ед-цы и их обследуют по более широкой программу. Эта выборка связана с многоступенчатой. На каждой ступени она м.б. многофазной.
34. Ошибки выборки и методы их расчета по среднему знач выборочн показ и по доле признака выбороч совок Ошибка репрезент-это расхожд мд хар-ми выборки и генер со-сти.Она зависит от численности выборки и вариации признака,методов отбора единиц выборочн совокупн.
Рассчитт два вида ошибок: Средняя(мю) и предел(дельта) Средняя: 1)по данным выб набл устан-ся величина выбор сред и выб дисперсии 2)опред сред ошибка выборки 3)с залданной вероятн P(t) наход предел ошибка выборки
35.сама(там много формул) 36. Способы распр резул выбор набл на генер совок. Конечн целью выб набл явл распростр полученных данных на генер совок,при этом исходят из тго,что сред и относ показатели полученные в выбор набл явл несмещенными и эф-ными хар-ками ген совокупности. В зависимости от цели исслед примен различ способы получения хар-к генер сов-сти по пок-лям выборки. Способ прямого расчета:при этом способе показ по генер совок рассчит путем умножения средн размеров признака или доли найденных в рез-те выб набл-ния с учетом их предельной ошибки на численность ед-ц генер совок
Способ поправочн ко-ов
Примен в случаях,когда целью выб набл явл уточнение данных сплошного учета,расчитыв попр ко-т путем сопоставл данных контрольного выбор набл и показателей сплошного набл,далее величина объема генер сов-стей корректир на поправ ко-т.
37. Понятие о рядах динамики,виды и правила построения Ряды динамики-ряды расположенных в хронологическом поярдке показателей характер развитие изучаемого явления во времени. Ряды динамики вкл 2 осн Эл-та: Показатель времени t при соотв уровню развития и y с индексом t Уровни рядов динамики выраж колич оценку развитич изучаемого явления во времени. Уровни базис периода(у0) а отчетного(у1) Дин ряды:моментные и интервальные. Момент отобр состояние изуч явлений на опред момент времени.Особенности момент рядов:уровни ряда повтор друг в друге,урни не отраж длину периода в течении которого сохр их размер,урни не облад свойством суммарности. Интерв ряды отобр состоян изучаемыъ явл за отдел интерв времени.Особен интер:урни не вовт др в др,отра длину периода,облад св-вом суммарности. В зависимости от исслед по-лей ребы бывают?абсол величин,относит и средних.С помощью рядов динамики решают след задачи: Хар-ка уравнений разв-я изучаемых явлений во времени,анализ динамики изуч явлений посредством системы стат показателей,выявлен осн тенденций развития и ее колич оценка,изучен периодич и сезонных колебаний,интерполяция и экстрополяция,т.е. прогнозирование.
38. Аналит показ дина ряда,спос их рас и взаимосвязь. В рез-те сопоставл уровней динам рядов вычисл аналит производные показателей,они могут быть расчит цепн и базис способом.При цепн каждый послед ур-нь сопост с предыд,а при базис с одним и тем же ур-нем принятым за базу сравнения. Абс прирост- разница знач 2ух уровней ряда. А)цепной Б)базисный Темп прироста- отношение 2 уровней ряда.
Tбi=П(Tц)i
|
||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.239.234 (0.011 с.) |


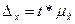 где t-коэф доверия
где t-коэф доверия
 для средней
для средней для доли
для доли
 (=у3-у0)
(=у3-у0) ;
; 



