Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА9.1. Понятие и виды статистических индексовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Индексы - это относительные величины, которые выражают соотношение уровней социально-экономических явлений и используются для решения таких задач, как: · обобщающая характеристика изменения одноименного показателя по разнородной совокупности во времени (индексы динамики), в пространстве (территориальные индексы) или по сравнению с некоторым заданным уровнем (например, планируемым или нормативным - индексы выполнения плана); · анализ влияния отдельных факторов на изучаемое явление; · оценка динамики среднего показателя по однородной совокупности, в том числе за счет изменений ее структуры. На основе индексов проводится оценка изменения средних показателей по однородной совокупности, например средней цены товара, продаваемого в разных регионах, в том числе за счет непосредственно роста уровня цен и за счет изменения структуры продаж. Статистические индексы классифицируются по следующим направлениям (рис. 10.1): · выбранной в знаменателе индекса базе сравнения; · степени агрегирования (или охвата) явления; · форме построения сводных индексов; · характеру исследуемой величины; · виду весов, выбранных в индексе; · периоду сравнения. Экономическое содержание выбранной базы сравнения позволяет провести деление всех индексов на динамические, территориальные и индексы сравнения с плановыми (нормативными) значениями показателей. Последняя группа включает в себя индексы планового задания [показывают степень увеличения (снижения) показателя, предусмотренную планом], индексы выполнения плана (показывают соотношение между фактическим значением показателя и его плановым уровнем), индексы сравнения с нормативными значениями (например, индексы выполнения норм расходов материала). По степени агрегирования, или охвата явления, индексы делятся на индивидуальные и сводные. Индивидуальный индекс характеризует изменение показателя у отдельной единицы совокупности (например, изменение цены на принтеры определенной марки). Сводный индекс выступает в качестве обобщенной характеристики изменения показателя в целом по всей совокупности разнородных единиц (изменение цен в целом на принтеры всех видов). Сводные индексы, в свою очередь, делятся на общие и групповые (субиндексы). Общие показывают изменение сложного явления в целом в рамках исследуемой совокупности, групповые - ее части. Например, если в качестве общего взять индекс потребительских цен, то субиндексом может являться индекс цен на продовольственные товары. 9.2. Индивидуальные индексы Индивидуальный индекс представляет собой относительный показатель, характеризующий изменение отдельного элемента сложного экономического явления. Методика исчисления индивидуальных индексов динамики социально-экономических показателей подобна методике расчета относительных величин: сравнивается абсолютное значение показателя в текущем и базисном периоде. Величина, изменение которой изучается с помощью индекса, называется индексируемой величиной. В индексной методологии принята следующая система обозначений: i - индивидуальный индекс; I - общий (сводный) индекс; q 0, q 1 -количество единиц (или физический объем) продукции (товаров) в натуральных единицах измерения; p 0, p 1 - цена единицы продукции (товара); z 0, z 1 - себестоимость единицы продукции; t 0, t 1 - затраты рабочего времени на производство единицы продукции (трудоемкость продукции); w 0, w 1 - количество продукции, выработанной одним работником в единицу времени (производительность труда); Т 1 и Т 0 - затраты труда на производство продукции (Т = t × q). Подстрочные обозначения «0» и «1» показывают временной период. Период времени, по отношению к которому производят сравнение, называют базисным и обозначают через «0», а период, сравниваемый с базисным, - отчетным и обозначают его через «1». Приведем примеры построения индивидуальных индексов: · индивидуальный индекс цен рассчитывается так:
Он показывает, как цена на данный товар в текущем периоде изменилась по сравнению с ценой этого же товара в базисном периоде; · индивидуальный индекс физического объема имеет вид
Аналогичным образом строятся индивидуальные индексы сравнения с плановыми или нормативными значениями, например индекс выполнения плана по объему продукции
где q пл. - количество единиц данного вида продукции, предусмотренное планом. В числителе и знаменателе территориальных индексов находятся значения показателя, относящиеся к двум сравниваемым территориям, например индивидуальный территориальный индекс цен на определенный товар будет иметь вид
где рА, рВ - цена данного товара соответственно на территориях А и В. Ниже представлены формулы расчета индивидуальных индексов наиболее часто используемых экономических показателей.
Пример 10.1. Магазин продал 1800 кг товара «А» по цене 210 руб. за килограмм в июле, а в июне - 1600 кг этого же товара по цене 200 руб. Определим индивидуальные индексы: · индивидуальный индекс физического объема реализованной продукции
· индивидуальный индекс цен
На основе проведенных расчетов можно сделать вывод, что в июле по сравнению с июнем объем реализации товара «А» увеличился в 1,125 раза, или на 12,5%, а цена этого товара - в 1,05 раза, или на 5%. 9.3. Агрегатные индексы При использовании индексного метода на практике чаще всего решают задачу нахождения не индивидуальных, а сводных индексов. Общий (сводный) индекс (I) представляет собой отношение уровней сложного экономического явления, состоящего из элементов, непосредственно несоизмеримых. Он дает обобщающую характеристику изменения одноименного показателя по разнородной совокупности во времени, в пространстве или по сравнению с некоторым заданным уровнем (например, планируемым или нормативным). В индексной теории по способу (форме) построения общие (сводные) индексы подразделяют на агрегатные, средние и индексы изменения среднего показателя. Последняя группа индексов имеет свою специфику, о ней мы будем говорить ниже. Основной формой построения индексов является агрегатная; средние индексы получаются в результате ее преобразования. В агрегатной формуле сводного индекса присутствуют два элемента: 1) индексируемая величина, изменение которой показывает индекс (обозначим ее через х); 2) некоторая постоянная величина, называемая весом индекса (f); с помощью весов несоизмеримые элементы сложного социально-экономического явления приводятся к сопоставимому виду. Веса в общем индексе необходимы, поскольку суммировать значение признака х по элементам разнородной совокупности неправомерно (например, нельзя суммировать объемы продаж различных товаров в розничной торговле в натуральных единицах измерения). Поэтому находят такой связанный с х показатель (f), при котором произведение х и f имеет экономическое содержание и может суммироваться по всем единицам разнородной совокупности [например, умножив количества товаров на их цены, получим объемы продаж в денежном выражении (товарооборот), которые можно суммировать по разным видам товаров]. Общая формула агрегатного индекса может быть записана следующим образом:
где х 1 и х 0 - значения индексируемой величины, соответственно, в отчетном и базисном периоде; f - вес или соизмеритель. Значения этого показателя у всех единиц совокупности при исчислении индекса должны быть взяты на уровне одного и того же периода - отчетного или базисного, с тем, чтобы индекс показал изменение только индексируемой величины. Таким образом, в числителе и знаменателе агрегатной формы индекса находятся просуммированные произведения двух величин, одна из которых - индексируемая величина (в числителе содержится значение, относящееся к отчетному периоду, а в знаменателе - к базисному), а другая - постоянная, являющаяся весом индекса. При этом суммируемых произведений столько, сколько единиц исследуемой совокупности входит в изучаемое явление. Но к какому периоду должны относиться веса индекса (f) - отчетному или базисному? В теории индексов обычно придерживаются следующих правил: · индексы качественных показателей строятся с весами отчетного периода. Тогда формула агрегатного индекса примет вид
· индексы количественных показателей строятся с весами базисного периода. Формула агрегатного индекса в этом случае имеет следующий вид:
Построение агрегатного индекса покажем на примере сводного (общего) индекса цен (Ip). В данном случае индексируемой величиной является цена, поэтому в числителе возьмем ее значение за отчетный период (р 1), а в знаменателе - за базисный (р 0). Непосредственно просуммировать цены отчетного периода и разделить их на сумму базисных цен мы не можем. Если же цену каждого товара умножить на его количество, то полученные произведения, характеризующие товарооборот, суммировать можно. Поскольку цена - качественный показатель, данные о количестве проданных товаров необходимо взять на уровне отчетного периода. Таким образом, получаем следующую формулу агрегатного индекса цен:
Пример 10.2. В таблице представлена следующая информация по ценам и количеству проданной молочной продукции:
Проведем расчет общего индекса цен по агрегатной формуле.
Следовательно, цены на молочную продукцию увеличились в 1,121 раза, или на 12,1%. Агрегатная форма построения индекса позволяет провести расчеты с учетом веса каждого товара в их общей совокупности. И для индивидуальных, и для общих индексов действует общее правило: индексы связаны между собой так же, как и индексируемые величины. Например, товарооборот - это произведение цены на количество реализованного товара. Точно такая же зависимость выполняется для индексов этих показателей:
Аналогично индекс затрат на производство продукции является произведением индекса себестоимости и индекса физического объема продукции:
Следует отметить, что в теории и практике статистики существует несколько подходов к решению проблемы выбора системы взвешивания. В частности, при построении агрегатных индексов цен используется несколько формул расчета этих показателей, названных по имени авторов, их разработавших. Наибольшую известность получили индексы цен Пааше, Ласпейреса и Фишера. При расчете индекса цен по формуле Пааше в качестве весов берутся количества продукции текущего периода:
С помощью этого индекса определяется изменение цен на товары, реализованные или приобретенные в текущем периоде. При расчете индекса цен по формуле Ласпейреса в качестве весов используются количества продукции базисного периода:
Данный индекс характеризует изменение цен на товары, реализованные в базисном периоде. По такой схеме обычно строятся индексы стоимости жизни, когда хотят оценить изменение цен на фиксированный набор товаров, обычно приобретаемых определенными группами населения. Выбор той или иной формулы для оценки динамики цен зависит от принятой в стране методологии расчета, имеющейся информации и целей исследования. Вопрос о том, какая из формул более точно характеризует изменение цен, не совсем корректен: каждый индекс предназначен для решения своей конкретной задачи. Вместе с тем желание получить один показатель для отражения динамики цен привело к появлению целого ряда работ, целью которых было найти идеальную формулу индекса. Наиболее известные работы в этой области принадлежат американскому ученому Ирвину Фишеру, который предложил свой подход к исчислению агрегатного индекса цен, а именно использовать среднюю геометрическую из индексов цен Пааше и Ласпейреса:
В данной формуле равноправно представлено количество продукции как базисного, так и текущего периодов. Это свойство позволяет применять данный индекс при исследовании цен за значительный промежуток времени, когда структура продукции претерпевает существенные изменения, и, строго говоря, не представляется возможным сделать обоснованный выбор в пользу весов базисного или отчетного периода. По этим же соображениям индекс Фишера часто используется для территориальных сопоставлений. Средние индексы В отличие от агрегатной формы индекса, средние индексы используются тогда, когда имеется информация об изменении индексируемой величины по отдельным единицам исследуемой совокупности (т. е. известны индивидуальные индексы). Средний индекс - это сводный индекс, вычисленный как средневзвешенная величина из значений индивидуальных индексов. Средний индекс получают путем преобразования агрегатного индекса. В зависимости от того, какие веса используются в соответствующей агрегатной формуле (базисного или отчетного периода), средний индекс рассчитывается по формуле средней арифметической или средней гармонической величины. Соответственно, исчисленные по одним и тем же данным агрегатный и средний индексы всегда равны. Рассмотрим, например, как получается средний индекс физического объема товарооборота. Его агрегатная формула имеет вид
Тогда, учитывая, что индивидуальный индекс представляет собой отношение
Получен индекс физического объема товарооборота в виде средней арифметической взвешенной из индивидуальных индексов, в которой в качестве весов используется товарооборот базисного периода (q 0 p 0). Итак, формула среднего арифметического индекса физического объема имеет вид
Обратимся теперь к индексу цен. Его агрегатная формула имеет вид
Из формулы индивидуального индекса цен
Получен средний гармонический индекс цен
Пример 10.3. По данным таблицы из примера 10.2 рассчитаем средние индексы. Для этого необходимо определить индивидуальные индексы и объем товарооборота по каждому виду молочной продукции (расчеты проведены в следующей таблице).
Исчислим средний гармонический индекс цен.
Средний арифметический индекс физического объема товарооборота равен
9.5. Анализ динамики среднего уровня показателя На формирование среднего уровня качественного показателя оказывают влияние два фактора: во-первых, изменение индивидуальных значений самой индексируемой величины в отчетном периоде по сравнению с базисным, и, во-вторых, изменение структуры исследуемой совокупности (уменьшение или увеличение доли единиц с более низким или более высоким уровнем этого показателя). Например, на динамику средней цены влияют изменения индивидуальных уровней цен и различия в структуре продаж отчетного периода по сравнению с базисным; на формирование среднего уровня фондоотдачи - изменения фондоотдачи отдельных видов основных фондов и доли основных фондов с более высоким (низким) уровнем фондоотдачи в общей их совокупности (структурный фактор). Относительное изменение среднего уровня качественного показателя характеризуется с помощью системы индексов переменного, постоянного состава и индекса структурных сдвигов, позволяющих оценить влияние каждого фактора на его динамику. Покажем общую схему построения системы индексов, характеризующих динамику среднего уровня качественного показателя. Индекс переменного состава отражает изменение среднего уровня качественного показателя за счет двух факторов. Пусть х - индексируемая величина, f - вес индекса. В общем виде этот индекс рассчитывается как отношение среднего уровня показателя в отчетном периоде к среднему уровню показателя в базисном периоде. Индекс переменного состава для любых качественных показателей может быть записан следующим образом:
Индекс постоянного (фиксированного) состава показывает, как в среднем изменилось значение качественного показателя у единиц совокупности при одинаковой фиксированной ее структуре. В общем виде его можно записать следующим образом:
Формула индекса влияния структурных сдвигов, представляющего собой отношение средних величин рассматриваемого качественного показателя, рассчитанных при структуре совокупности отчетного и базисного периодов при базисном уровне качественного показателя, выглядит следующим образом:
Поскольку индекс переменного состава показывает изменение исследуемого явления за счет всех факторов, то между индексами существует следующая взаимосвязь: I пер.сост. = I пост.сост. × I стр.сд.. Так, при изучении изменения средней цены товара (например, продаваемого в разных регионах) индекс переменного состава можно записать следующим образом:
Подставляя вместо
На его величину оказывают влияние два фактора: изменение цены товара в каждом регионе и структуры продаж. Абсолютное изменение среднего уровня цены товара за счет двух факторов покажет разность между числителем и знаменателем рассматриваемого индекса:
Индекс цен постоянного (фиксированного) состава показывает изменение средней цены товара только за счет изменений цен в каждом регионе. Индекс цен постоянного состава имеет вид
Абсолютное изменение среднего уровня цены за счет изменения индексируемой величины покажет разность между числителем и знаменателем данного индекса
Индекс структурных сдвигов позволяет оценить влияние на формирование среднего уровня цены изменений в структуре продаж товара:
Абсолютное изменение среднего уровня качественного показателя (в данном случае средней цены) за счет структурных сдвигов
Пример 10.4. В таблице приведены цены и объемы продаж товара «А» в трех регионах.
Индекс цен переменного состава равен
Общее измерение средней цены в абсолютном выражении
За счет действия двух факторов средняя цена увеличилась на 11,1%, или на 6,31 руб. Для определения влияния первого фактора (цен в каждом регионе) на динамику средней цены исчислим индекс цен постоянного состава:
Тогда влияние первого фактора в абсолютном выражении можно определить как
Таким образом, в результате изменения цен товара «А» в отдельных регионах его средняя цена увеличилась на 10,8%, или на 6,15 руб. Влияние на анализируемый показатель структурных изменений в структуре продаж товара «А» покажет индекс структурных сдвигов
В абсолютном выражении
В результате изменения структуры продаж товаров по регионам средняя цена возросла на 0,3%, или 16 копеек. Проверим взаимосвязь индексов и абсолютных приростов:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 2303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.107.223 (0.009 с.) |






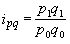












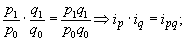




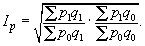

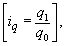 получим [ q 1 = iq × q 0] Подставим это выражение в формулу агрегатного индекса
получим [ q 1 = iq × q 0] Подставим это выражение в формулу агрегатного индекса

 выразим
выразим  и, подставив в формулу агрегатного индекса, получим
и, подставив в формулу агрегатного индекса, получим








 выражения для расчета средних уровней цен товара отчетного и базисного периодов, получим его развернутую формулу
выражения для расчета средних уровней цен товара отчетного и базисного периодов, получим его развернутую формулу