Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выявление основной тенденции ряда динамики.Содержание книги
Поиск на нашем сайте
При изучении в рядах динамики основной тенденции развития явления применяются различные приемы и методы: метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания. Наиболее эффективный метод выявления основной тенденции развития - аналитическое выравнивание. В этом случае уровни ряда динамики выражаются в виде функции времени:
Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Функция выбирается на основе анализа характера закономерности динамики данного явления. Колеблемость динамических рядов. Основная тенденция показывает, как систематические факторы воздействуют на уровень ряда динамики, а колеблемость уровней тренда служит мерой воздействия остаточных факторов. Мерой колеблемости динамического ряда выступает средний квадрат отклонений фактических уровней, исчисленных по тренду. Ее можно измерить показателем среднего квадратического отклонения. Относительной мерой колеблемости является коэффициент вариации, равный отношению среднего квадратического отклонения к среднему уровню ряда. Измерение сезонных колебаний. При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по внутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или несколько лет. При изучении сезонных колебаний используются специальные показатели - индексы сезонности (Is):
где
Совокупность исчисленных для каждого годового цикла индексов сезонности характеризует сезонную волну развития явления во внутригодовой динамике и наглядно может быть представлена графическим методом. При наличии ярко выраженной тенденции развития (увеличение или уменьшение уровней из года в год) применимы другие способы измерения сезонных колебаний, в частности, индексы сезонности определяются на основе методов, которые позволяют исключать влияние тенденции роста (падения). В таких случаях фактические данные сопоставляются с выровненными, и индексы сезонности определяются по формуле:
где yi - исходные уровни ряда;
n - число годовых периодов. Выравнивание может быть проведено методом аналитического выравнивания или методом скользящей средней Пример 1. Имеются следующие данные о динамике производства тканей в одном из регионов за 1999 - 2003 гг.: Аналитические показатели уровня ряда получаются сравнением уровней между собой. Сравниваемый уровень принято называть текущим, а уровень, с которым происходит сравнение, - базисным. За базу сравнения обычно принимают предыдущий уровень или начальный уровень ряда динамики. При сравнении каждого уровня с предыдущим получаются цепные показатели. Если же сравнение ведется с одним уровнем (базой), то показатели называются базисными. Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель - абсолютный прирост (D y). Его величина определяется как разность двух сравниваемых уровней и вычисляется следующим образом: D y = уi - у 0 - базисные показатели; D y = уi - уi -1 - цепные показатели, где уi - уровень i -го периода (кроме первого); у 0 - уровень базисного периода; уi -1 - уровень предыдущего периода. В примере 1 абсолютный прирост по сравнению с 1999 г. составит: · в 2000 г. – D y = 267 – 256 = 11 (млн м2); · в 2001 г. - D y = 279 - 256 = 23 (млн м2) и т. д. Рассчитаем цепные показатели абсолютного прироста для примера 1. Абсолютный прирост составит: · в 2000 г. по сравнению с 1999 г. - D y = 267 - 256 = 11 (млн м2); · в 2001 г. по сравнению с 2000 г. - D y = 279 - 267 = 12 (млн м2) и т. д. Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному. Этот показатель называется коэффициентом роста, или темпом роста (Т р), и выражается в процентах:
Если Т р больше 100%, уровень растет, если меньше - уровень уменьшается. Т р - всегда положительное число. В примере 1 темп роста составит: · в 2000 г. по сравнению с базисным 1999 г.:
· в 2001 г. по сравнению с базисным 1999 г.:
Рассчитаем цепные показатели темпа роста для примера 1. Темп роста составит: · в 2000 г. по сравнению с базисным 1999 г.:
· в 2001 г. по сравнению с 2000 г.:
Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Т пр), который рассчитывается как отношение абсолютного прироста к базисному или предыдущему уровню:
Темп прироста может быть вычислен также путем вычитания из темпов роста 100%, т. е. Т пр = Т р - 100%. Для примера 1 рассчитаем темп прироста: · в 2000 г. по сравнению с базисным 1999 г.: T пр = 104,3% - 100% = 4,3%; · в 2001 г. по сравнению с базисным 1999 г.: T пр = 109% - 100% = 9% и т. д. Показатель абсолютного значения 1% прироста (|%|) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах.
или 0,01 yi - 1. В примере 1 абсолютное значение прироста 1% составит: · в 2000 г. по сравнению с 1999 г.: |%| = 0,01 y 1999 г. = 0,01 × 256 = 2,56 (млн м2); · в 2001 г. по сравнению с 2000 г.: |%| = 0,01 y 2000 г. = 0,01 × 267 = 2,67 (млн м2) и т. д. Приведенная в примере 1 таблица с вычислениями характеристик изменения уровней позволяет проводить анализ данного динамического ряда. В примере 1 мы имеем интервальный ряд динамики с равноотстоящими уровнями во времени, поэтому средний уровень ряда рассчитаем по формуле средней арифметической простой:
где n -число периодов. Средний объем производства тканей за пять лет составил: Средний абсолютный прирост определяется по формуле: В примере 1 среднегодовой прирост производства тканей за 1999 - 2003 гг. равен: Среднегодовой темп роста вычисляется по формуле средней геометрической: где n - число коэффициентов роста. Среднегодовой темп роста производства тканей за 1999 - 2003 г. (пример 1) рассчитаем двумя способами: Среднегодовой темп прироста получим, вычтя из среднего темпа роста 100%. В примере 1:
Если интервальный ряд динамики имеет неравноотстоящие уровни, то средний уровень ряда вычисляется по формуле средней арифметической взвешенной:
где t - число периодов времени, в течение которых уровень не изменяется. Для моментного ряда с равноотстоящими уровнями средний уровень ряда вычисляется по формуле средней хронологической. Пример 2. Известны товарные остатки магазина на 1-е число каждого месяца 2003 г.
В данном случае мы имеем моментный ряд с равноотстоящими уровнями, поэтому средний уровень ряда определим по формуле средней хронологической, которая рассчитывается следующим образом:
где n - число уровней ряда. Средние товарные остатки за полугодие составят:
Пример 3. Известна численность работников предприятия на следующие даты:
В данном случае мы имеем моментный ряд динамики с разноотстоящими уровнями, поэтому средний уровень ряда рассчитаем по формуле средней хронологической для разноотстоящих уровней динамики:
Среднесписочная численность работников составит:
|
||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 408; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.200.142 (0.007 с.) |



 - средняя для каждого месяца за изучаемый период;
- средняя для каждого месяца за изучаемый период;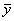 - общий средний месячный уровень за изучаемый период.
- общий средний месячный уровень за изучаемый период.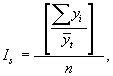
 - базисные показатели;
- базисные показатели; - цепные показатели.
- цепные показатели.
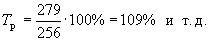

 - базисные показатели;
- базисные показатели; - цепные показатели.
- цепные показатели.

 - итог суммирования уровней за весь период;
- итог суммирования уровней за весь период;