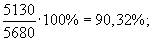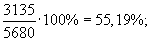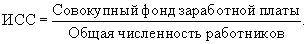Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА.1.1. Краткая история статистикиСодержание книги
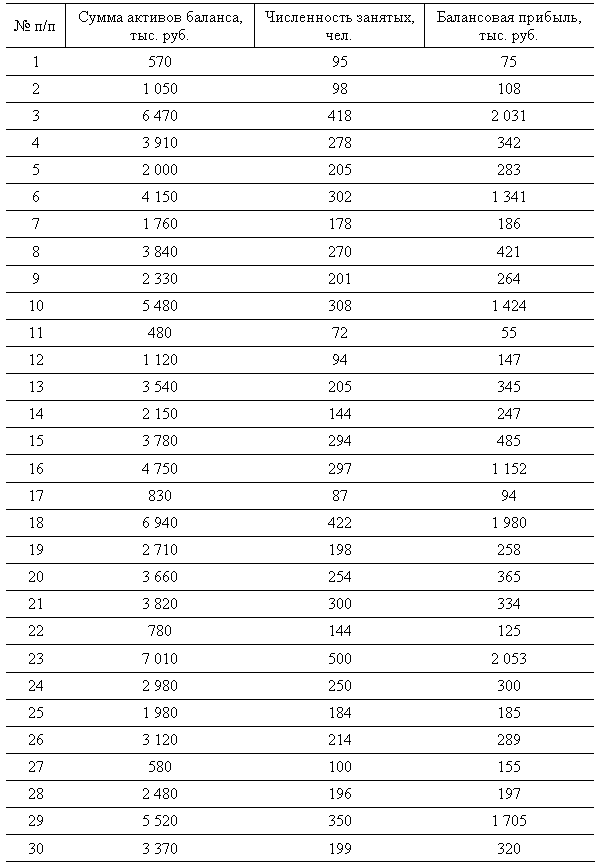
Поиск на нашем сайте Способы статистического наблюдения Известны следующие способы получения статистической информации об объекте исследования: · непосредственное наблюдение; · способ, основанный на изучении документов; · опрос. При непосредственном наблюдении производят подсчет, взвешивание, обмер единицы наблюдения и т.п. В результате этих действий устанавливается некий факт, сведения о котором заносятся в статистический формуляр. Способ наблюдения, основанный на изучении документов,- наиболее точный, особенно если документами учетного характера является бухгалтерская документация. При опросе регистрируемые сведения заносятся в статистический формуляр со слов опрашиваемого. Как правило, никакими документами они при этом не подтверждаются. ТЕМА 3 В результате статистического наблюдения получают первичные данные о единицах изучаемой совокупности, которые на следующем этапе исследования обобщаются и систематизируются путем сводки и группировки. Сводку необходимо проводить по следующим этапам: · выбор группировочного признака; · определение порядка формирования групп; · разработка системы статистических показателей для характеристики групп и объекта в целом; · разработка макетов статистических таблиц для представления результатов сводки. Сводка и группировка - второй этап исследования. С помощью метода группировок решаются следующие задачи: · выделение социально-экономических типов явлений; · изучение структуры явления и структурных сдвигов, происходящих в нем; · выявление связи и зависимости между явлениями. Статистические группировки могут быть типологическими, структурными и аналитическими. По числу группировочных признаков различают простые и сложные группировки. Сложные группировки в свою очередь бывают комбинационными и многомерными. Построение группировки начинается с определения группировочного признака или группировочных признаков. Группировочными могут быть как качественные, так и количественные признаки. Первые отражают состояние единицы совокупности (пол человека, семейное положение, форма собственности или организационно-правовая форма предприятия и т. д.), вторые имеют числовые выражения (возраст человека, доход семьи, объем производства и т. д.). После выбора основания группировки следует решить вопрос о количестве групп, которое зависит от задачи исследования и вида признака, положенного в основание группировки, численности совокупности, степени вариации признака. После определения количества групп следует установить интервал группировки. Величина интервала представляет собой разность между верхней и нижней границами интервала. Интервалы группировки в зависимости от их величины бывают равные и неравные. Среди последних выделяют прогрессивно возрастающие, произвольные и специализированные. Результаты сводки и группировки материалов статистического наблюдения обычно оформляют в виде таблиц. Статистическая таблица - это таблица, которая содержит сводную числовую характеристику исследуемой совокупности по одному или нескольким существенным признакам, взаимосвязанным логикой экономического анализа. Статистическая таблица имеет подлежащее и сказуемое. Подлежащее статистической таблицы характеризует объект исследования. В подлежащем дается перечень единиц совокупности либо групп исследуемого объекта по существенным признакам. Сказуемое статистической таблицы образует система показателей, которыми характеризуется объект изучения, т. е. подлежащее таблицы. В зависимости от структуры подлежащего различают статистические таблицы простые, в подлежащем которых дается простой перечень единиц совокупности, и сложные, подлежащее которых содержит группы единиц совокупности по одному (групповые) или нескольким (комбинационные) количественным либо атрибутивным признакам. Рассмотрим методику построения аналитической группировки на примере 30 коммерческих банков одного из регионов России (табл. 3.1). Основные показатели деятельности 30 коммерческих банков
В качестве группировочного признака возьмем сумму активов баланса и по этому показателю построим ранжированный ряд от минимального значения до максимального. Определим число групп с использованием формулы Стерджесса: n = 1 + 3,322 lg N, где n - число групп; N - число единиц совокупности. n = 1 + 3,322 lg30 = 5,90, или примерно 6 групп. Затем определяем величину интервала по формуле
Существуют следующие правила записи числа интервала. Если величина интервала, рассчитываемая по формуле, представляет собой величину, которая имеет один знак до запятой (например, 0,63; 2,158; 6,74), то полученные значения целесообразно округлить до десятых и использовать в качестве шага интервала. Если рассчитанная величина имеет две значащие цифры до запятой и несколько знаков после запятой (например, 18,475), то это значение необходимо округлить до целого числа. В случае, когда величина интервала представляет собой трех- и более значное число, ее следует округлить до ближайшего числа, кратного 100 или 50. Так как в рассматриваемом примере рассчитанная величина интервала представляет собой четырехзначное число, округлим его до 1100 тыс. руб. Далее обозначим границы групп с равными интервалами: · группа 1: до 1 600; · группа 2: 1 600-2 700; · группа 3: 2 700-3 800; · группа 4: 3 800-4 900; · группа 5: 4 900-6 000; · группа 6: 6 000 и более. После того как выбран группировочный признак - сумма активов баланса, устанавливаем число групп - 6 и образуем группы. Затем отбираем показатели, которые характеризуют группы, и определяем величины показателей по каждой группе. Результаты группировки заносятся в таблицу, определяются общие итоги по совокупности единиц наблюдения по каждому показателю (табл. 3.2). Группировка коммерческих банков одного из регионов России
Структурная группировка коммерческих банков на основе данных табл. 3.2 представлена в табл. 3.3. Структурная группировка коммерческих банков
Из таблицы 3.3 видно, что в основном преобладают средние банки - 60%, на долю которых приходится 60,4% суммы активов баланса и 60,8% занятых работников. Более конкретный анализ взаимосвязи показателей можно сделать на основе аналитической группировки (табл. 3.4). Аналитическая группировка коммерческих банков
Данные табл. 3.4 характеризуют взаимосвязь суммы активов баланса, численности занятых работников и балансовой прибыли банков. Чем больше сумма активов баланса банка, тем больше численность его работников и балансовая прибыль. В шестой группе банков средняя численность занятых в 4,5 раза больше, чем в первой группе, а балансовая прибыль - в 18,7 раз. Следовательно, крупные банки работают эффективнее. Аналитические группировки позволяют установить связь и определить направление между результативным и факторными признаками. Но часто этого бывает недостаточно, так как на самом деле на изменение величины результативного признака оказывает влияние множество факторов, действующих в разных направлениях. Для изучения таких многофакторных связей используют многомерные группировки. Их целью является расчленение совокупности социально-экономических явлений на качественно однородные группы по большому числу признаков одновременно и определение на основе этих групп влияния факторных признаков на результативный. В основу построения многомерной группировки положен принцип перехода от величин, имеющих определенную размерность (рубли, тонны, гектары и т. д.), к безразмерным относительным величинам. Абсолютные значения результативного признака заменяются отношениями а абсолютные значения факторных признаков - отношениями Если связь между результативным и факторными признаками обратная, то для каждой единицы объекта исследования определяется величина На основе отношений pij исчисляется показатель Этот показатель и будет основанием многомерной группировки, которая покажет взаимосвязь между множеством исследуемых факторных признаков и одним результативным признаком. На основе многомерной группировки можно построить уравнение регрессии, которое отразит количественно степень связи между признаками. Таблица 3.2 Структура работников по стажу работы на предприятии
Важную роль в статистическом анализе играют аналитические группировки. С их помощью определяют наличие связи между признаками и ее направление. При этом один из признаков является результативным, а другой - факторным. Результативный признак меняется под воздействием факторного признака. При построении аналитической группировки в качестве группировочного признака всегда выбирают факторный признак. В каждой выделенной группе рассчитывают среднее значение результативного признака. Например, в табл. 3.3 компании сгруппированы по величине затрат на рекламу. В каждой группе определен средний размер товарооборота. Из таблицы видно, что чем больше внимания компании уделяют рекламе, тем значительнее результаты их деятельности, выражающиеся в объеме товарооборота. Таблица 3.3 Распределение компаний по затратам на рекламу и объему товарооборота
Связь между признаками называется прямой, если с ростом значений факторного признака увеличиваются значения результативного признака. Связь является обратной, если увеличение значений факторного признака приводит к уменьшению значений результативного признака. В нашем примере рост затрат на рекламу вызвал увеличение объемов товарооборота, значит между этими признаками наблюдается прямая связь. В зависимости от количества признаков, по которым проводится группировка, различают простые и сложные группировки. Если группировка проводится по одному признаку, то она называется простой (см. табл. 3.1, 3.2). Если единицы совокупности группируются сразу по двум или более признакам, то такая группировка называется сложной. При этом внутри групп, образованных по одному признаку, единицы совокупности подразделяются на подгруппы по другому признаку. Примером сложной группировки является группировка учащихся на потоке по двум признакам - полу и возрасту. Ее результаты могут быть представлены в виде таблицы (табл. 3.4). Распределение учащихся на потоке по полу и возрасту
Вторичная группировка данных. На практике часто возникают ситуации, когда по имеющимся сгруппированным данным требуется построить новую группировку. При этом, как правило, массив первичных данных оказывается недоступным. Тогда прибегают к методам вторичной группировки данных. Вторичной группировкой называется перегруппировка уже сгруппированных данных без обращения к массиву первичных данных. Для этой цели применяются два подхода: объединение первоначальных интервалов, если границы новых и старых групп совпадают, и долевая перегруппировка данных при несовпадении границ. Метод объединения первоначальных интервалов продемонстрируем на следующем примере. Предположим, что исходные данные представляют собой ряд, приведенный в табл. 3.5. Распределение работников фирмы по размеру заработной платы
Перегруппируем данные и образуем новые интервалы: «2000–4000», «4000–6000», «6000 и выше». Поскольку границы новых и старых интервалов совпадают, легко видеть, что в первый новый интервал «2000-4000» попадут работники первого и второго интервалов исходной группировки (16 + 40 = 56 чел.), во второй новый интервал - работники третьего и четвертого интервалов исходной группировки (65 + 58 = 123 чел.), в третий новый интервал - работники двух последних интервалов (44 + 17 = 61 чел.). Результаты перегруппировки представлены в табл. 3.6. Распределение работников фирмы по размеру заработной платы (вторичная группировка)
Долевая перегруппировкавка базируется на принципе равномерности распределения единиц наблюдения внутри границ интервальных групп. В результате ее проведения рассчитывают, какая часть единиц наблюдения перейдет из старой интервальной группы в новую. Пример 3.1. «Перегруппируем данные табл. 3.5 и образуем новые интервалы: «2000–3400»; «3400–4800»; «4800–6200»; «6200 и выше». Распределим единицы совокупности по новым интервалам. В первый новый интервал войдут из исходной группировки все единицы первого интервала и часть единиц из второго интервала. Эту часть мы определяем следующим образом. Новая граница «3400» разбивает второй интервал на два отрезка: «3000–3400» и «3400–4000». Находим, какую долю составляет длина отрезка «3000–3400» от длины второго интервала. Она равна Во второй новый интервал войдут оставшиеся от второго интервала исходной группировки 24 единицы (40 – 16) и часть единиц из третьего интервала. Для этого мы находим, какую долю составляет отрезок «4000–4800» от длины третьего интервала «4000–5000». Она равна В третий интервал вторичной группировки войдут оставшиеся 13 единиц (65 – 52 = 13) третьего интервала исходной группировки, все единицы ее четвертого интервала (58 ед.) и 9 единиц пятого интервала В последний интервал новой группировки войдут оставшиеся 35 единиц (44 – 9 = 35) пятого интервала и все 17 единиц последнего интервала, т.е. 52 единицы (35 + 17). При проверке правильности расчетов видим, что сумма единиц совокупности осталась равной 240. Результаты вторичной группировки приведены в следующей таблице. Распределение работников фирм по размеру заработной платы
Результаты группировки собранных статистических данных, как правило, представляются в видеиде рядов распределения. Ряд распределения - это упорядоченное распределение единиц совокупности на группы по изучаемому признаку. Ряды распределения делятся на атрибутивные и вариационные, в зависимости от признака, положенного в основу группировки. Если признак качественный, то ряд распределения называется атрибутивным. Примером атрибутивного ряда является распределение предприятий и организаций по формам собственности (см. табл. 3.1). Если признак, по которому строится ряд распределения, количественный, то ряд называется вариационным. Вариационный ряд распределения всегда состоит из двух частей: вариант и соответствующих им частот (или частостей). Вариантой называется значение, которое может принимать признак у единиц совокупности, частотой - количество единиц наблюдения, обладающих данным значением признака. Сумма частот всегда равна объему совокупности. Иногда вместо частот рассчитывают частости - это частоты, выраженные либо в долях единицы (тогда сумма всех частостей равна 1), либо в процентах к объему совокупности (сумма частостей будет равна 100%). Вариационные ряды бывают дискретными и интервальными. У дискретных рядов (табл. 3.7) варианты выражены конкретными числами, чаще всего целыми. Распределение работников по времени работы в страховой компании
В интервальных рядах (см. табл. 3.2) значения показателя задаются в виде интервалов. Интервалы имеют две границы: нижнюю и верхнюю. Интервалы могут быть открытыми и закрытыми. У открытых нет одной из границ, так, в табл. 3.2 у первого интервала нет нижней границы, а у последнего - верхней. При построении интервального ряда в зависимости от характера разброса значений признака используют как равные интервальные промежутки, так и неравные (в табл. 3.2 представлен вариационный ряд с равными интервалами).и). Если признак принимает ограниченное число значений, обычно не больше 10, строят дискретные ряды распределения. Если вариант больше, то дискретный ряд теряет свою наглядность; в этом случае целесообразно использовать интервальную форму вариационного ряда. При непрерывной вариации признака, когда его значения в определенных пределах отличаются друг от друга на сколь угодно малую величину, также строят интервальный ряд распределения. Рассмотрим методику построения дискретных вариационных рядов на примере. Пример 3.2. Имеются следующие данные о количественном составе 60 семей: 2 3 3 1 4 2 3 3 1 5 2 4 3 2 2 1 2 3 4 5 2 2 1 3 4 3 3 3 6 6 3 3 6 1 3 4 3 4 4 5 3 3 2 2 1 3 2 5 5 2 4 3 6 1 2 2 3 1 3 4. Для того чтобы получить представление о распределении семей по числу их членов, следует построить вариационный ряд. Поскольку признак принимает ограниченное число целых значений строим дискретный вариационный ряд. Для этого сначала рекомендуется выписать все значения признака (число членов в семье) в порядке возрастания (т.е. провести ранжирование статистических данных): 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 6 6 6. Затем необходимо подсчитать число семей, имеющих одинаковый состав. Число членов семей (значение варьирующего признака) - это варианты (будем их обозначать через х), число семей, имеющих одинаковый состав,- это частоты (будем их обозначать через f). Результаты группировки представим в виде следующего дискретного вариационного ряда распределения:
Покажем методику построения интервальных вариационных рядов распределения на следующем примере.ре. Пример 3.3. В результате статистического наблюдения получены следующие данные о средней величине процентной ставки 50 коммерческих банков (%):
Как видим, просматривать такой массив данных крайне неудобно, кроме того, не видно закономерностей изменения показателя. Построим интервальный ряд распределения. 1) Определим число интервалов. Число интервалов на практике часто задается самим исследователем исходя из задач каждого конкретного наблюдения. Вместе с тем его можно вычислить и математически по формуле Стерджесса n = 1 + 3,322 lg N, где n - число интервалов; N - объем совокупности (число единиц наблюдения). Для нашего примера получим: n = 1 + 3,322 lg N = 1 + 3,322 lg 50 = = 6,6» 7. 2) Определим величину интервалов (i) по формуле
где х max - максимальное значение признака; х min - минимальное значение признака. Для нашего примера
Интервалы вариационного ряда наглядны, если их границы имеют «круглые» значения, поэтому округлим величину интервала 1,9 до 2, а минимальное значение признака 12,3 до 12,0. 3) Определим границы интервалов. Интервалы, как правило, записывают таким образом, чтобы верхняя граница одного интервала являлась одновременно нижней границей следующего интервала. Так, для нашего примера получим: 12,0–14,0; 14,0–16,0; 16,0–18,0; 18,0–20,0; 20,0–22,0; 22,0–24,0; 24,0–26,0. Подобная запись означает, что признак непрерывный. Если же варианты признака принимают строго определенные значения, например, только целые, но их количество слишком велико для построения дискретного ряда, то можно создать интервальный ряд, где нижняя граница интервала не будет совпадать с верхней границей следующего интервала (это будет означать, что признак дискретный). Например, в распределении работников предприятия по возрасту можно создать следующие интервальные группы лет: 18–25, 26–33, 34–41, 42–49, 50–57, 58–65, 66 и более. Кроме того, в нашем примере мы могли бы сделать первый и последний интервалы открытыми, т.е. записать: до 14,0; 24,0 и выше. 4) По исходным данным построим ранжированный ряд. Для этого запишем в порядке возрастания значения, которые принимает признак. Результаты представим в таблице: Ранжированный ряд величин процентной ставки коммерческих банков*
*В таблице чертой отделены значения признаков, попадающих в один и тот же интервал. 5. Подсчитаем частоты. При подсчете частот может возникнуть ситуация, когда значение признака попадет на границу какого-либо интервала. В таком случае можно руководствоваться правилом: данная единица приписывается к тому интервалу, для которого ее значение является верхней границей. Так, значение 16,0 в нашем примере будет относиться ко второму интервалу. Результаты группировки, полученные в нашем примере, оформим в таблице. Распределение коммерческих банков по величине кредитной ставки
В последней графе таблицы представлены накопленные частоты, которые получают путем последовательного суммирования частот, начиная с первой (например, для первого интервала - 5, для второго интервала 5 + 9 = 14, для третьего интервала 5 + 9 + 4 = 18 и т.д.). Накопленная частота, например, 33, показывает, что у 33 банков кредитная ставка не превышает 20% (верхняя граница соответствующего интервала). Относительные величины Относительные величины представляют собой результат деления абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических процессов и явлений. Относительные статистические величины бывают следующих видов: · динамики; · расчетного задания; · выполнения расчетного задания; · структуры; · координации; · интенсивности уровня экономического развития, сравнения. Относительная величина динамики (ОВД) - отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом:
Относительная величина расчетного задания (ОВРз) - отношение величины расчетного задания на период к достигнутой величине прошлого периода:
Относительная величина выполнения расчетного задания (ОВРв.з) -отношение величины, достигнутой в отчетном периоде, к величине расчетного задания:
Относительная величина структуры (ОВС) - соотношение структурных частей изучаемого объекта и их целого:
Относительная величина координации (ОВК) - отношение одной части совокупности к другой части этой же совокупности:
Относительная величина интенсивности (ОВИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к показателю присущей ему среды:
Разновидностью относительной величины интенсивности является относительная величина уровня экономического развития, характеризующая производство продукции в расчете на душу населения и играющая важную роль в оценке развития экономики государства. Относительная величина сравнения (ОВСр) - соотношение одного и того же абсолютного показателя, характеризующего разные объекты:
Рассмотрим методику расчета основных видов относительных показателей на конкретных примерах. Пример 1. Имеются следующие данные по предприятию:
Рассчитаем относительные величины динамики: а) по производственному капиталу:
б) по оборотным средствам:
в) по собственным средствам:
г) по заемным средствам:
Рассчитанные относительные величины динамики показывают, что на 1 января 2004 г. по сравнению с 1 января 2003 г. производственный капитал предприятия вырос на 6,51%; в то же время оборотные средства уменьшились на 9,68%, а собственные - на 18,18%; заемные средства увеличились на 0,79%. Пример 2. Воспользуемся данными примера 1 и рассчитаем относительные величины структуры. 1. Доля оборотных средств в общей стоимости производственного капитала предприятия составит: а) на 1 января 2003 г.:
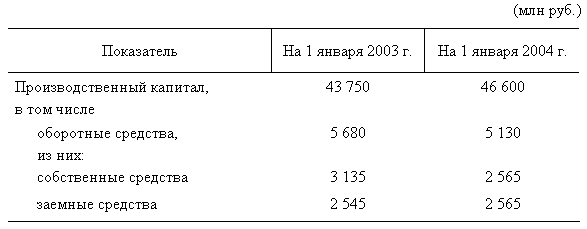
б) на 1 января 2004 г.:
2. Доля собственных средств в общей стоимости оборотных средств составит: а) на 1 января 2003 г.:
б) на 1 января 2004 г.:
Из полученных показателей видно, что на предприятии доля оборотных средств в общей стоимости производственного капитала снизилась на 1,98% и на 1 января 2004 г. составила 11%. Доля собственных средств в общей стоимости оборотного капитала на 1 января 2003 г. составила 55,19%, а на 1 января 2004 г. снизилась и составила 50%, т. е. только на 50% необходимые предприятию запасы и затраты обеспечиваются собственными средствами. Пример 3. Возьмем данные примера 1 и рассчитаем относительные величины координации. 1. Соотношение заемных и собственных средств предприятия составит: а) на 1 января 2003 г.:
б) на 1 января 2004 г.:
Этот показатель свидетельствует о том, что на каждый рубль собственных средств предприятия на 1 января 2003 г. приходилось 81,18 коп. заемных средств, а на 1 января 2004 г. -1 руб. 2. Соотношение собственных и заемных средств составит: а) на 1 января 2003 г.:
б) на 1 января 2004 г.:
Этот показатель характеризует финансовую устойчивость или платежеспособность предприятия, т. е. его способность рассчитываться по своим обязательствам. Пример 4. В 2002 г. оборот торговой фирмы составил 2500 млн руб. В 2003 г. фирма рассчитывала увеличить оборот до 3200 млн руб. Фактический оборот фирмы в 2003 г. составил 2800 млн руб. Рассчитаем относительные величины расчетного задания, выполнения расчетного задания и динамики и определим их взаимосвязь:
Между относительными величинами расчетного задания, выполнения расчетного задания и динамики существует следующая взаимосвязь: ОВРз × ОВРв.з= ОВД. В нашем примере: 1,28× 0,875 =1,12, или 1,12 × 100% = 112%; или
Пример 5. Рассчитаем относительную величину сравнения на основании следующих данных. В 2002 г. инвестиции в экономику Российской Федерации составили: Кипра - 2,327 млн дол. США; США - 1,133 млн дол. США.
Инвестиции Кипра в экономику Российской Федерации в 2 раза превышают инвестиции США. Пример 6. Рассчитаем относительный показатель уровня экономического развития на основании следующих данных: в 2002 г. валовой внутренний продукт Российской Федерации составил 10 863,3 млрд руб., среднегодовая численность населения - 145,18 млн человек. Отсюда искомый показатель равен:
Следовательно, в 2002 г. ВВП на душу населения составил 74 826 руб. ТЕМА 5 Средняя величина - обобщающая характеристика однотипных явлений по одному из варьирующих признаков Определить среднюю можно через (ИСС) или ее логическую формулу:
Для изучения и анализа социально-экономических явлений процессов применяются различные средние величины средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя кубическая, а также структурные средние - мода, медиана, квартили, децили. Средние могут рассчитываться в двух вариантах: взвешенные и невзвешенные (табл. 5.1). Виды степенных средних
В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в % или долях единицы). Тогда используют формулу средней:
В интервальном вариационном ряду для расчета средней арифметической взвешенной определяются и используются значения середины интервалов. Рассмотрим методологию применения разных видов степенных средних на основе расчета средней заработной платы по двум предприятиям вместе: за январь, февраль и за два месяца. Исходные данные представлены в табл. 5.2.
Определим исходные соотношения средней для показателя «средняя заработная плата»:
За январь мы располагаем данными о средней заработной плате и численности работников, т. е. нам известен знаменатель исходного соотношения, но неизвестен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность работников. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
где xi - i -й вариант осредняемого признака; fi - вес i -го варианта. За февраль мы имеем только данные о средней заработной плате и фонде оплаты труда, т. е. нам известен числитель исходного соотношения, но неизвестен знаменатель. Численность работников по каждому предприятию можно получить делением фонда оплаты труда на среднюю заработную плату. Тогда средняя заработная плата в целом по двум предприятиям будет рассчитываться по формуле средней гармонической взвешенной:
где w I = x ifi За два месяца средняя заработная плата по двум предприятиям определяется по формуле средней арифметической простой (невзвешенной), так как веса (f) отсутствуют или равны.
где n - число единиц, или объем совокупности. Таким образом, исходя из приведенных данных, были применены разные виды степенных средних. Средняя геометрическая используется в анализе динамики для определения среднего темпа рос
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.038 с.) |

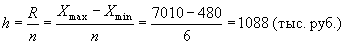




 где
где 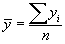
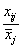 , где
, где  . В результате такой замены получается матрица отношений.
. В результате такой замены получается матрица отношений. .
. где k - число факторных признаков.
где k - число факторных признаков. . Значит, от 40 единиц, находившихся во втором интервале исходной группировки, следует взять для нового первого интервала 16 единиц
. Значит, от 40 единиц, находившихся во втором интервале исходной группировки, следует взять для нового первого интервала 16 единиц  . Тогда первый новый интервал будет содержать 32 единицы (16 + 16).
. Тогда первый новый интервал будет содержать 32 единицы (16 + 16). . Значит, от 65 единиц следует взять для второго нового интервала 52 единицы
. Значит, от 65 единиц следует взять для второго нового интервала 52 единицы  . Итак, второй интервал новой группировки будет содержать 76 единиц (24 + 52).
. Итак, второй интервал новой группировки будет содержать 76 единиц (24 + 52).