
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Шкала оценок парных коэффициентов корреляцииСодержание книги
Поиск на нашем сайте
Примечание: положительное значение коэффициента говорит о том, что связь между признаками прямая, отрицательное - обратная. Следующий этап корреляционного анализа связан с расчетом множественного (совокупного)коэффициента корреляции. Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной и совокупностью других переменных, рассматриваемых в корреляционном анализе. Если изучается связь между результативным признаком y и лишь двумя факторными признаками х 1 и х 2, то для вычисления множественного коэффициента корреляции можно использовать следующую формулу, компонентами которой являются парные коэффициенты корреляции:
где r - парные коэффициенты корреляции. 11.3. Регрессионный анализ Регрессионный анализ - это статистический метод исследования зависимости случайной величины Y от переменных Хj. При построении парной регрессии (с одной факторной переменной) обычно используются следующие функции: 1) линейная 2) степенная 3) показательная 4) параболическая 5) гиперболическая 6) логарифмическая где а 0 - свободный коэффициент уравнения регрессии; а 1 - параметр уравнения регрессии. Однако в действительности любой результативный показатель испытывает воздействие не одного, как в случае парной корреляции, а нескольких факторов, поэтому зачастую строят модели множественной регрессии, которые принимают вид: 1) линейная (наиболее часто встречающаяся модель): 2) степенная: 3) показательная: 4) параболическая: 5) гиперболическая: где а 0 - свободный коэффициент регрессии; аj (j = 1, 2, …, k) - параметры регрессионного уравнения, называемые коэффициентами регрессии. Для того чтобы правильно выбрать тип регрессионного уравнения, следует знать условный закон распределения зависимой переменной Y. На основе графика не всегда удается определить его однозначно, поэтому строят несколько регрессионных моделей, а затем по определенным критериям определяют лучшую модель. Если в проводимом исследовании можно ограничиться построением линейной модели, выбирают ее. Такая популярность и предпочтительность объясняется очень просто: математический аппарат линейных уравнений наиболее разработан, а сами модели легко интерпретируемы. Критерием нахождения значений коэффициентов регрессии аj является следующее требование: сумма квадратов отклонений наблюдаемых «игреков» от «игреков», рассчитанных по уравнению регрессии, должна быть минимальной. Параметры регрессионной модели должны быть такими, чтобы на графике корреляционного поля линия регрессии оказалась там, где точки фактических наблюдений наибольшим образом сконцентрированы, т. е. проходила бы на минимальном удалении от них. В виде формулы это требование записывается следующим образом: Метод нахождения значений коэффициентов регрессии по приведенному критерию называется методом наименьших квадратов (МНК). Если имеется только один факторный признак, строится так называемая парная регрессия, выражающаяся уравнением прямой
Коэффициент регрессии а 1 показывает, на какую величину в среднем изменится результативный признак Y, если переменную Х увеличить на единицу ее собственного измерения. Свободный член уравнения а 0 характеризует усредненное влияние неучтенных в модели факторов (определяет начальные условия развития). Для нахождения параметров уравнения прямой воспользуемся методом наименьших квадратов. Для расчета параметров линейного уравнения регрессии решим следующую систему нормальных уравнений:
После решения системы и нахождения параметров а 0 и а 1 данные параметры подставляют в уравнение прямой. Рассчитанные по этому уравнению значения Пример 12.3. Рассчитаем парный коэффициент корреляции и построим уравнение регрессии на основе следующих данных.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.3.204 (0.007 с.) |




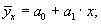
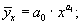




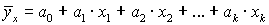 ;
;






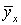 называются теоретическими (выравненными) значениями у.
называются теоретическими (выравненными) значениями у.


