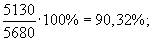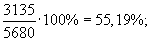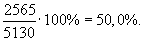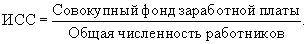Табличное представление статистических данных

Статистическую информацию, прошедшую стадию сводки и группировки, представляют в виде статистических таблиц.

Каждая статистическая таблица (способ представления статистической информации) имеет подлежащее и сказуемое. Подлежащее представляет собой перечень единиц статистического наблюдения или их групп, которые характеризуются статистическими показателями. Данные показатели являются сказуемым статистической таблицы. На макете таблицы это выглядит следующим образом:

Макетстатистической таблицы

№ п/п	Подлежащее таблицы	Сказуемое таблицы
А			…
…

 

При необходимости подлежащее и сказуемое таблицы можно поменять местами, если это удобнее и нагляднее воспринимается потребителем.

В зависимости от разработки подлежащего выделяются простые, групповые и комбинационные таблицы.

Простое подлежащее статистической таблицы представляет собой простой перечень единиц наблюдения, которыми могут быть даты (годы, кварталы, месяцы, дни), предприятия, страны, территории и т.д. Например, в табл. 4.1 подлежащим являются отдельные виды продовольственных товаров, которые характеризуются сказуемым - ценами на конец года.

Средние потребительские цены на отдельные виды продовольственных товаров

Вид продовольственных товаров	Цены на конец года, руб. за кг
Говядина (кроме бескостного мяса)	93,41	115,77
Куры (кроме куриных окорочков)	69,94	81,35
Рыба замороженная неразделанная	48,68	55,76
Масло сливочное	93,96	102,42
Масло подсолнечное	39,10	40,06
Молоко цельное пастеризованное, за литр	15,52	17,35
Яйца, за десяток	28,44	24,50
Сахар-песок	19,69	19,69
Чай черный байховый	183,01	193,61
Хлеб и булочные изделия из пшеничной муки высшего сорта	21,61	22,24
Картофель	8,12	9,72
Яблоки	34,09	36,87
Водка обыкновенного качества, за литр	134,94	148,89

 

Подлежащее статистической таблицы может быть представлено в виде определенной группировки по одному атрибутивному или количественному признаку; такие таблицы называются групповыми. Примером является табл. 4.2, где подлежащее - уставный капитал - представлено в виде интервальных групп.

 

Распределение коммерческих банков Российской Федерации по величине уставного капитала в 2006 г.

Уставный капитал, млрд руб.	Количество банков
на начало года	на конец года
До 10
10-15
15-20 20-25 25 и выше
Итого

 

Подлежащее комбинационной статистической таблицы представляет собой сложную группировку по двум или более признакам. Так, табл. 4.3 содержит распределение предприятий по двум признакам: «Объем основных промышленно-производственных фондов» и «Уровень рентабельности продукции».

Распределение промышленных предприятий города по величине основных производственных фондов
и уровню рентабельности продукции в 2006 г.

Объем основных промышленно-производственных фондов, млн руб.	Уровень рентабельности продукции, %	Количество предприятий, ед.
До 5	До 10 10-20 20-30 30 и более
Итого по группе
5-10	До 10 10-20 20-30 30 и более
Итого по группе
10-20	До 10 10-20 20-30 30 и более
Итого по группе
Всего

 

В данном случае представлена группировка по двум признакам: объему основных промышленно-производственных фондов и уровню рентабельности выпускаемой продукции. Возможно включение и большего числа признаков, но в этом случае таблица станет слишком громоздкой и плохо воспринимаемой.

Сказуемое статистической таблицы также может быть простым и сложным. В таблицах с простой разработкой сказуемого показатели характеризуют подлежащее независимо друг от друга (например, табл. 4.4).

Крупнейшие города России
(по состоянию на 1 января 2005 г.)

Город	Численность населения, тыс. чел.	Расстояние до Москвы, км
Москва	10 407	-
Санкт-Петербург	4 600
Новосибирск	1 406	3 191
Екатеринбург	1 304	1 667
Нижний Новгород	1 289
Омск	1 143	2 555
Самара	1 133	1 098
Казань	1 110
Челябинск	1 095	1 919
Ростов-на-Дону	1 058	1 226
Уфа	1 036	1 519

 

Численность населения и расстояние между Москвой и другими городами России - независимые показатели.

Сложное сказуемое представляет собой комбинацию нескольких признаков (например, табл. 4.5).

Состав депутатов Государственной Думы созыва 2004-2007 гг.
(по состоянию на 1 января 2006 г.)

	Депутаты, всего	В том числе
мужчины	женщины
Всего
в том числе по фракциям:
Единая Россия
Коммунистическая партия Российской Федерации
Либерально-демократическая партия России
Родина
Родина (Народная Воля - Социалистическая Единая партия России)
Депутаты, не входящие в зарегистрированные депутатские объединения

 

Пол депутатов связан в таблице с принадлежностью к статусу депутата.

Существуют строгие правила оформления статистических таблиц, которых следует придерживаться. Приведем важнейшие из них:

· в правом верхнем углу пишется слово «Таблица…» и указывается ее номер;

· ниже, посередине строки, шрифтом, отличным от основного, приводится название таблицы, в котором указывается ее аналитическая цель (Динамика…), объект наблюдения (в табл. 4.5 - это депутаты Государственной Думы), территориальная и временная принадлежность информации, помещенной в таблице. Кроме того, в названии при необходимости содержатся и некоторые уточнения: если это распределение, то приводятся показатели, по которым оно проводится, как, например, в табл. 4.6:

Распределение убыточных предприятий и организаций Москвы
по отраслям экономики и крупности бизнеса в 2004 г.

Регион

Число убы­точных пред­приятий и организаций - всего, ед.

В том числе по отраслям экономики

промышленность

сельское хозяйство

строитель­ство

транспорт и связь

торговля и общественное питание

другие отрасли

малые предпр.

средние и крупные предпр.

малые предпр.

средние и крупные предпр.

малые предпр.

средние и крупные предпр.

малые предпр.

средние и крупные предпр.

малые предпр.

средние и крупные предпр.

малые предпр.

средние и крупные предпр.

Москва - всего,

в том числе по админ. округам:

Центральный

Северо- Западный

Северо-Восточный и т.д.

 

· статистическая таблица не должна быть слишком громоздкой (это затрудняет ее восприятие), строки и графы должны иметь название, не допускающее двойного толкования. Если строк и граф много, то целесообразно их пронумеровать: графы с подлежащим - прописными буквами алфавита (А, Б и т.д., если подлежащее сложное), графы со сказуемым и строки - арабскими цифрами (табл. 4.7).

Макет статистической таблицы

п/п	Название подлежа­щего, единица его измерения	Сказуемое первое, единица его измерения	Сказуемое второе, единица его измерения	Сказуемое третье, единица его изме­рения
	А
	Перечень единиц наблюдения либо их групп	0,00	…	-
	1,01	-	…	…
	…	х	…	…
…	х	…	…	…
Итого	-

 

· все графы таблицы должны иметь единицы измерения. Если используется одна и та же единица измерения для всех граф, ее проставляют в верхнем правом углу над таблицей либо указывают в скобках после названия таблицы. Цифры в пределах одной графы округляют до одной разрядности;

· если явление в данной позиции отсутствует, в соответствующей клетке таблицы ставят прочерк (-). Если сведений по данной позиции не имеется, ставят три точки (…).

Цифры, меньшие используемой единицы измерения и округления, обозначаются «0,0» (после запятой столько нулей, сколько разрядов используется для округления).

В не подлежащих заполнению клетках таблицы проставляют «х»;

· внизу под таблицей приводятся необходимые примечания. Они могут содержать сведения об источниках информации, методологии расчета показателей (если данные таблицы имеют несопоставимую методологию расчета) и др.;

· если статистическая таблица не умещается на отведенном для нее листе по длине или ширине, то в первом случае, продолжая ее на следующем листе, в правом верхнем углу над таблицей следует сделать пояснение: «Продолжение». На новом листе продолжается перечень единиц наблюдения либо из группы, а также переносятся либо названия граф (сказуемое), либо (если есть) нумерация граф (табл. 4.8).

Оформление таблицы, не уместившейся по длине

(продолжение)

п/п	А				…
… …	Продолжается перечень единиц наблюдения либо их групп

 

Если таблица не помещается по ширине, то на новый лист переносится подлежащее таблицы, и далее помещаются названия граф, не поместившиеся на предыдущей странице (табл. 4.9).

Оформление таблицы, не уместившейся по ширине

(продолжение)

п/п	А	…			…
	Перечень единиц наблюдения либо их групп (переносится с предыду­щего листа)

4 ТЕМА 4.1. Абсолютные величины

Статистическое наблюдение, независимо от его масштабов и целей, всегда дает информацию о тех или иных социально-экономических явлениях и процессах в виде абсолютных показателей, т.е. показателей, представляющих собой количественную характеристику социально-экономических явлений и процессов в условиях качественной определенности. Качественная определенность абсолютных показателей заключается в том, что они напрямую связаны с конкретным содержанием изучаемого явления или процесса, с его сущностью. В связи с этим абсолютные показатели и абсолютные величины должны иметь определенные единицы измерения, которые наиболее полно и точно отражали бы их сущность (содержание).

Абсолютные показатели являются количественным выражением признаков статистических явлений. Например, рост — это признак, а его значение — это показатель роста.

Абсолютный показатель должен характеризовать размер изучаемого явления или процесса в данном месте и в данное время, он должен быть «привязан» к какому-нибудь объекту или территории и может характеризовать либо отдельную единицу совокупности (отдельный объект) — предприятие, рабочего, либо группу единиц, представляющую часть статистической совокупности, либо статистическую совокупность в целом, например, численность населения в стране, и т.п. В первом случае речь идет об индивидуальных абсолютных показателях, а во втором — о сводных абсолютных показателях.

Индивидуальными называют абсолютные величины, характеризующие размеры отдельных единиц совокупности (например, количество деталей, изготовленных одним рабочим за смену, число детей в отдельной семье). Их получают непосредственно в процессе статистического наблюдения и фиксируют в первичных учетных документах. Индивидуальные показатели получают в процессе статистического наблюдения за теми или иными явлениями и процессами как результат оценки, подсчета, замера фиксированного интересующего количественного признака.

Сводные абсолютные величины получаются, как правило, путем суммирования отдельных индивидуальных величин. Сводные абсолютные показатели получают в результате сводки и группировки значений индивидуальных абсолютных показателей. Так, например, в процессе переписи населения органы государственной статистики получают итоговые абсолютные данные о численности населения страны, о распределении его по регионам, по полу, возрасту и т.д.

К абсолютным показателям также можно отнести показатели, которые получаются не в результате статистического наблюдения, а в результате какого-либо расчета. Как правило, данные показатели — это разность между двумя абсолютными показателями. Например, естественный прирост (убыль) населения находится как разность между числом родившихся и числом умерших за определенный период времени; прирост продукции за год — как разность между объемом произведенной продукции на конец года и объемом произведенной продукции на начало года. При составлении долгосрочных прогнозов развития экономики страны рассчитывают предположительные данные о материальных, трудовых, финансовых ресурсах. Как видно из примеров, эти показатели будут абсолютными, т.к. имеют абсолютные единицы измерения.

Абсолютные величины отражают естественную основу явлений, т.е. выражают либо численность единиц изучаемой совокупности, ее отдельных составных частей, либо их абсолютные размеры в натуральных единицах, вытекающих из их физических свойств (масса, длина и т.п.), или в единицах измерения, вытекающих из их экономических свойств (стоимость, затраты труда). Следовательно, абсолютные величины всегда имеют определенную размерность.

Кроме того, абсолютные статистические показатели всегда выражаются в натуральных, стоимостных и трудовых единицах измерения в зависимости от сущности описываемых ими процессов и явлений.

Натуральные измерители характеризуют явления в свойственной им натуральной форме и выражаются в мерах длины, массы, объема и т.п. или количеством единиц, числом событий. К натуральным можно отнести такие единицы измерения, как тонна, килограмм, метр и т.д., например: объем жилищного строительства составил 2000 м².

В ряде случаев используются комбинированные единицы измерения, представляющие собой произведение двух величин, выраженных в различных размерностях. Так, например, производство электроэнергии измеряется в киловатт-часах, грузооборот — в тонно-километрах и т.п.

В группу натуральных единиц измерения входят и так называемые условно натуральные единицы измерения. Их применяют для получения суммарных абсолютных величин в случае, когда индивидуальные величины характеризуют отдельные разновидности продукции, близкие по своим потребительским свойствам, но отличающиеся, например, содержанием жира, спирта, калорийностью и т.п. При этом одна из разновидностей продукции принимается за условный натуральный измеритель и к ней с помощью переводных коэффициентов, выражающих соотношение потребительских свойств (иногда трудоемкости, себестоимости и т.д.) отдельных разновидностей, приводятся все разновидности этого продукта.

Трудовые единицы измерения используют для характеристики показателей, которые позволяют оценить затраты труда, отражают наличие, распределение и использование трудовых ресурсов, например, трудоемкость выполненных работ в человеко-днях.

Натуральные, а иногда и трудовые измерители не позволяют получить сводные абсолютные показатели в условиях разнородной продукции. В этом плане универсальными являются стоимостные единицы измерения, которые дают стоимостную (денежную) оценку социально-экономическим явлениям, характеризуют стоимость определенной продукции или объема выполненных работ. Например, в денежной форме выражаются такие важные для экономики страны показатели, как национальный доход, ВВП, а на уровне предприятия — прибыль, собственные и заемные средства.

Наибольшее предпочтение в статистике отдается стоимостным единицам измерения, т.к. стоимостный учет является универсальным, однако он не всегда приемлем.

Абсолютные показатели могут быть рассчитаны во времени и пространстве. Например, динамика численности населения Российской Федерации с 1991 по 2004 г. отражается временным фактором, а уровень цен на хлебобулочные изделия по регионам РФ за 2004 г. характеризуется пространственным сравнением.

При учете абсолютных показателей во времени (в динамике) их регистрация может быть осуществлена на определенную дату, т.е. какой-либо момент времени (стоимость основных средств предприятия на начало года) и за какой-либо период времени (число родившихся за год). В первом случае показатели являются моментальными, во втором — интервальными.

С точки зрения пространственной определенности абсолютные показатели делят следующим образом: общие территориальные, региональные и локальные. Например, объем ВВП — общий территориальный показатель, объем ВРП (валовой региональный продукт) — региональный признак, численность занятых в городе — локальный признак, т.е. первая группа показателей характеризует страну в целом, региональные — конкретный регион, локальные — отдельный город, населенный пункт и т.д.

Абсолютные показатели не дают ответа на вопрос, какую долю имеет та или иная часть в общей совокупности, не могут охарактеризовать уровни планового задания, степень выполнения плана, интенсивность того или иного явления, т.к. они не всегда пригодны для сравнения и поэтому часто используются лишь для расчета относительных величин.

Относительные величины

Относительные величины представляют собой результат деления абсолютного показателя на другой и выражают соотношение между количественными характеристиками социально-экономических процессов и явлений.

Относительные статистические величины бывают следующих видов:

· динамики;

· расчетного задания;

· выполнения расчетного задания;

· структуры;

· координации;

· интенсивности уровня экономического развития, сравнения.

Относительная величина динамики (ОВД) - отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом:

Относительная величина расчетного задания (ОВР_з) - отношение величины расчетного задания на период к достигнутой величине прошлого периода:

Относительная величина выполнения расчетного задания (ОВР_в.з) -отношение величины, достигнутой в отчетном периоде, к величине расчетного задания:

Относительная величина структуры (ОВС) - соотношение структурных частей изучаемого объекта и их целого:

Относительная величина координации (ОВК) - отношение одной части совокупности к другой части этой же совокупности:

Относительная величина интенсивности (ОВИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к показателю присущей ему среды:

Разновидностью относительной величины интенсивности является относительная величина уровня экономического развития, характеризующая производство продукции в расчете на душу населения и играющая важную роль в оценке развития экономики государства.

Относительная величина сравнения (ОВС_р) - соотношение одного и того же абсолютного показателя, характеризующего разные объекты:

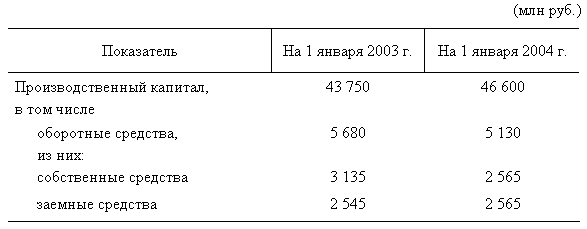
Рассмотрим методику расчета основных видов относительных показателей на конкретных примерах.

Пример 1. Имеются следующие данные по предприятию:

Рассчитаем относительные величины динамики:

а) по производственному капиталу:

б) по оборотным средствам:

в) по собственным средствам:

г) по заемным средствам:

Рассчитанные относительные величины динамики показывают, что на 1 января 2004 г. по сравнению с 1 января 2003 г. производственный капитал предприятия вырос на 6,51%; в то же время оборотные средства уменьшились на 9,68%, а собственные - на 18,18%; заемные средства увеличились на 0,79%.

Пример 2. Воспользуемся данными примера 1 и рассчитаем относительные величины структуры.

1. Доля оборотных средств в общей стоимости производственного капитала предприятия составит:

а) на 1 января 2003 г.:

б) на 1 января 2004 г.:

2. Доля собственных средств в общей стоимости оборотных средств составит:

а) на 1 января 2003 г.:

б) на 1 января 2004 г.:

Из полученных показателей видно, что на предприятии доля оборотных средств в общей стоимости производственного капитала снизилась на 1,98% и на 1 января 2004 г. составила 11%.

Доля собственных средств в общей стоимости оборотного капитала на 1 января 2003 г. составила 55,19%, а на 1 января 2004 г. снизилась и составила 50%, т. е. только на 50% необходимые предприятию запасы и затраты обеспечиваются собственными средствами.

Пример 3. Возьмем данные примера 1 и рассчитаем относительные величины координации.

1. Соотношение заемных и собственных средств предприятия составит:

а) на 1 января 2003 г.:

б) на 1 января 2004 г.:

Этот показатель свидетельствует о том, что на каждый рубль собственных средств предприятия на 1 января 2003 г. приходилось 81,18 коп. заемных средств, а на 1 января 2004 г. -1 руб.

2. Соотношение собственных и заемных средств составит:

а) на 1 января 2003 г.:

б) на 1 января 2004 г.:

Этот показатель характеризует финансовую устойчивость или платежеспособность предприятия, т. е. его способность рассчитываться по своим обязательствам.

Пример 4. В 2002 г. оборот торговой фирмы составил 2500 млн руб. В 2003 г. фирма рассчитывала увеличить оборот до 3200 млн руб. Фактический оборот фирмы в 2003 г. составил 2800 млн руб.

Рассчитаем относительные величины расчетного задания, выполнения расчетного задания и динамики и определим их взаимосвязь:

Между относительными величинами расчетного задания, выполнения расчетного задания и динамики существует следующая взаимосвязь:

ОВР_з × ОВР_в.з= ОВД.

В нашем примере:

1,28× 0,875 =1,12, или 1,12 × 100% = 112%;

или

Пример 5. Рассчитаем относительную величину сравнения на основании следующих данных. В 2002 г. инвестиции в экономику Российской Федерации составили:

Кипра - 2,327 млн дол. США;

США - 1,133 млн дол. США.

Инвестиции Кипра в экономику Российской Федерации в 2 раза превышают инвестиции США.

Пример 6. Рассчитаем относительный показатель уровня экономического развития на основании следующих данных: в 2002 г. валовой внутренний продукт Российской Федерации составил 10 863,3 млрд руб., среднегодовая численность населения - 145,18 млн человек. Отсюда искомый показатель равен:

Следовательно, в 2002 г. ВВП на душу населения составил 74 826 руб.

ТЕМА 5 Средняя величина - обобщающая характеристика однотипных явлений по одному из варьирующих признаков

Определить среднюю можно через (ИСС) или ее логическую формулу:

Для изучения и анализа социально-экономических явлений процессов применяются различные средние величины средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя кубическая, а также структурные средние - мода, медиана, квартили, децили. Средние могут рассчитываться в двух вариантах: взвешенные и невзвешенные (табл. 5.1).

Виды степенных средних

В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в % или долях единицы). Тогда используют формулу средней:

В интервальном вариационном ряду для расчета средней арифметической взвешенной определяются и используются значения середины интервалов.

Рассмотрим методологию применения разных видов степенных средних на основе расчета средней заработной платы по двум предприятиям вместе: за январь, февраль и за два месяца. Исходные данные представлены в табл. 5.2.

Определим исходные соотношения средней для показателя «средняя заработная плата»:

За январь мы располагаем данными о средней заработной плате и численности работников, т. е. нам известен знаменатель исходного соотношения, но неизвестен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность работников. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:

где x_i - i -й вариант осредняемого признака;

f_i - вес i -го варианта.

За февраль мы имеем только данные о средней заработной плате и фонде оплаты труда, т. е. нам известен числитель исходного соотношения, но неизвестен знаменатель. Численность работников по каждому предприятию можно получить делением фонда оплаты труда на среднюю заработную плату. Тогда средняя заработная плата в целом по двум предприятиям будет рассчитываться по формуле средней гармонической взвешенной:

где w _I = x _if_i

За два месяца средняя заработная плата по двум предприятиям определяется по формуле средней арифметической простой (невзвешенной), так как веса (f) отсутствуют или равны.

где n - число единиц, или объем совокупности.

Таким образом, исходя из приведенных данных, были применены разные виды степенных средних.

Средняя геометрическая используется в анализе динамики для определения среднего темпа роста.

Средняя квадратическая и степенные средние более высоких порядков используются при расчете ряда статистических показателей, характеризующих вариацию и взаимосвязь.