
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕМА7.1. Понятие рядов распределенияСодержание книги
Поиск на нашем сайте
Рядами распределения называются группировки особого вида, при которых по каждому признаку, группе признаков или классу признаков известны численность единиц в группе либо удельный вес этой численности в общем итоге. Ряды распределения могут быть построены или по количественному, или по атрибутивному признаку. Ряды распределения, построенные по количественному признаку, называются вариационными рядами. Ряд распределения может быть построен по непрерывно варьирующему признаку (признак может принимать любые значения в рамках какого-либо интервала) и по дискретно варьирующему признаку (принимает строго определенные целочисленные значения). Анализ рядов распределения осуществляется с помощью следующих показателей (показатели центра распределения). Средняя арифметическая взвешенная
где хi - середина интервала:
Медиана (Ме) - середина ранжированного ряда. В интервальном вариационном ряду медиана рассчитывается по формуле:
где XMe - нижняя граница медианного интервала; h - ширина интервала; SMe - 1 - накопленная частота интервала, предшествующего медианному; fMe - частота медианного интервала. Мода (Мо) - наиболее часто встречающееся значение признака в совокупности. В интервальном вариационном ряду мода находится в интервале с максимальной частотой и рассчитывается по формуле, которую мы уже приводили:
где XMo - нижняя граница модального интервала; fMo - частота модального интервала; fMo - 1 - частота интервала, предшествующего модальному; fMo + 1 - частота интервала, следующего за модальным. Квартили (Q) делят ранжированный ряд на четыре равные части: первый квартиль (Q 1) включает значения признака, не превышающие 25% единиц совокупности, второй квартиль (Q 2) — совпадает с медианой (Ме), третий квартиль (Q 3) — значения признака, не превышающие 75% единиц совокупности (рис. 8.3).
Децили (D) делят ранжированный ряд на десять равных частей: первым децилем (D 1) является значение признака, которое не превышает 10% единиц совокупности, вторым (D 2) — 20%, третьим (D 3) — 30% и т.д. При этом пятый дециль (D 5) совпадает с медианой и вторым квартилем (Q 2) (рис. 8.4).
Медиана, квартили и децили относятся к группе квантилей. Квантили — это показатели, которые делят вариационные ряды на определенное количество равных частей. Среди них, помимо названных, также имеются квинтили, которые делят ряд на пять равных частей, перцентили — на сто и т.д. Структурные показатели не зависят от того, имеются ли в статистической совокупности аномальные (резко выделяющиеся) наблюдения. И если средняя величина при их наличии теряет свою практическую значимость, то информативность медианы наоборот усиливается — она начинает выполнять функции средней, т.е. характеризовать центр совокупности. Способы расчета рассматриваемых структурных показателей зависят от вида вариационного ряда. Рассмотрим их подробнее.
|
||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 410; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.187.115 (0.009 с.) |




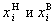 - нижняя и верхняя границы интервалов соответственно.
- нижняя и верхняя границы интервалов соответственно.






