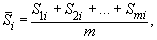Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы сезонных колебаний уровней динамического рядаСодержание книги
Поиск на нашем сайте
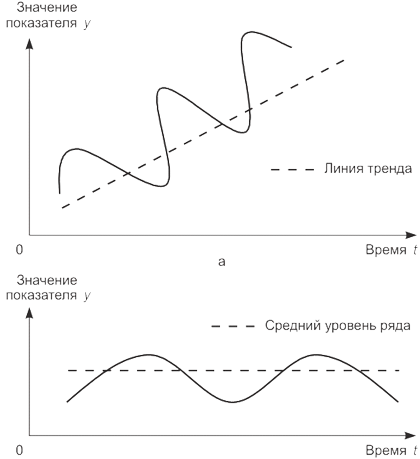
На практике в рядах динамики часто наблюдают некие устойчивые периодические колебания уровней либо вокруг линии тренда, либо по отношению к среднему уровню ряда. Причем эти колебания регулярно повторяются на протяжении некоторого периода: значения показателя возрастают или убывают в зависимости от момента времени, а затем по истечении некоторого временного срока, называемого циклом, возвращаются на свои предыдущие позиции (если колебания происходят вокруг среднего уровня ряда), либо повторяется характер их изменения (если значения уровней колеблются вокруг линии тренда (рис. 9.3а, б). В зависимости от длины цикла различают периодические колебания: циклические (долгопериодические, когда длина цикла составляет несколько лет), сезонные (внутригодичные колебания по месяцам или кварталам года), недельные, дневные (регулярные колебания по дням недели), часовые (в зависимости от часа дня). Сезонные колебания наиболее ярко проявляются в торговле (классическим примером является продажа овощей, фруктов и ягод, носящая сезонный характер), а также в производстве отдельных видов продукции (например, производство мороженого, кондитерских изделий), в потреблении электроэнергии и т. д. Периодические колебания изучают с помощью индексов сезонности. Строго говоря, термин «индексы сезонности» подразумевает, что индексы будут строиться для изучения периодических колебаний показателя по месяцам или кварталам в течение календарного года, т. е. для изучения сезонных колебаний. Но методология построения данной группы индексов позволяет их использовать и при изучении других видов периодических колебаний, таких как циклические, дневные, недельные, часовые.
Известны два способа определения индексов сезонности: 1)по отношению к среднему уровню, если периодические колебания показателя происходят вокруг его среднего уровня, т. е. анализируемые данные не имеют общей тенденции развития (метод постоянной средней);
При методе постоянной средней индексы сезонности находят по формуле
где
Покажем порядок расчета индексов сезонности по отношению к среднему уровню на примере изучения сезонных колебаний объема платных услуг населению по месяцам года. Исходные данные и результаты расчетов приведены в табл. 9.17 Расчет индексов сезонности
Средние уровни · для января:
· для февраля:
Общий средний уровень объема платных услуг населению за четыре года можно определить: · как среднюю арифметическую из полученных средних
· как среднюю арифметическую из четырех средних уровней, исчисленных для каждого года:
Тогда индексы сезонности для каждого месяца равны: · для января:
· для февраля:
Графическое изображение полученных индексов сезонности будет характеризовать «сезонную волну» в изменении рассматриваемого показателя (рис. 9.4).
Если прогнозируется, что в 2007 г. объем платных услуг увеличится до 210 млн руб. в год, то используя индексы сезонности можно оценить, какой будет величина этого показателя в каждом месяце данного года (т. е. составить прогноз на каждый месяц): · определим средний месячный уровень:
· рассчитаем предполагаемое значение показателя по месяцам 2007 г.: · для января: 17,5 × 1,06 = 18,55 (млн руб.); · для февраля: 17,5 × 0,964 = 16,87 (млн руб.) и т. д. В тех случаях, когда в ряду динамики наблюдается достаточно ярко выраженная тенденция роста его уровней (т. е. ряд содержит тренд), более правильно рассчитывать индексы сезонности методом переменной средней по следующей формуле:
где yti - фактическое значение показателя для i -го периода года t; m - число лет; Алгоритм расчета следующий: 1) по эмпирическим данным, применяя метод аналитического выравнивания, находят уравнение тренда; 2) на основе уравнения тренда, подставляя в него соответствующие значения условного показателя времени, рассчитывают выравненные уровни динамического ряда; 3) находят частные индексы сезонности как отношение эмпирических значений уровней ряда к соответствующим выровненным значениям
4) рассчитывают среднюю арифметическую величину из полученных индексов сезонности для каждого из одноименных моментов времени (например, если приведены данные за четыре года, то для каждого месяца получим четыре частных индекса сезонности, из которых находят среднюю)
где т - число одноименных моментов времени, соответствующее числу лет. Рассчитаем индексы сезонности по данным о реализации товаров группы «А» населению за два года (табл. 9.18).
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 389; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.25.100 (0.006 с.) |

 2)по отношению к тренду, если эмпирические данные содержат помимо периодических колебаний и общую тенденцию в своем развитии (метод переменной средней).
2)по отношению к тренду, если эмпирические данные содержат помимо периодических колебаний и общую тенденцию в своем развитии (метод переменной средней).
 - средний уровень показателя для момента (периода) времени i;
- средний уровень показателя для момента (периода) времени i; - îáùèé ñðåäíèé óðîâåíü ïîêàçàòåëÿ çà âåñü èññëåäóåìûé ïåðèîä âðåìåíè.
- îáùèé ñðåäíèé óðîâåíü ïîêàçàòåëÿ çà âåñü èññëåäóåìûé ïåðèîä âðåìåíè.
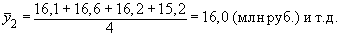
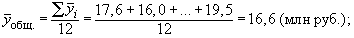






 - значение показателя для i -го периода внутри t -го года, определенное методом аналитического выравнивания;
- значение показателя для i -го периода внутри t -го года, определенное методом аналитического выравнивания;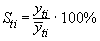 - частные индексы сезонности для i -го периода каждого года t;
- частные индексы сезонности для i -го периода каждого года t;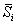 - средний индекс сезонности для i -го периода внутри года (месяца или квартала).
- средний индекс сезонности для i -го периода внутри года (месяца или квартала).