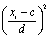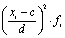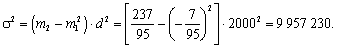Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
ТЕ6.1. Абсолютные и относительные показатели вариацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим две совокупности сотрудников рекламных агентств. Распределение сотрудников первого агентства по уровню месячной заработной платы представлено в табл. 7.1. Распределение сотрудников первого агентства
Распределение сотрудников второго агентства по уровню месячной заработной платы представлено в табл. 7.2. Распределение сотрудников второго агентства
Рассчитаем средний уровень заработной платы: · для первого агентства:
· для второго агентства:.
Как видим, средние в двух совокупностях практически совпадают между собой (с разницей в 1 руб.). Однако если вы вдруг случайно встретите сотрудников этих агентств и поинтересуетесь уровнем оплаты их труда, то вас заверят, что платят у них вовсе не одинаково! Почему?! Оказывается, что разброс значений вокруг средней в этих совокупностях абсолютно разный. Значит, такой характеристики, как средняя, вовсе не достаточно, чтобы делать выводы о совокупности. Для этого используют показатели вариации. Вариацией называется изменчивость значений признака у единиц статистической совокупности. Для измерения величины вариации используются абсолютные и относительные показатели вариации. К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение. Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака R = x max – x min. Среднее линейное отклонение (
Для сгруппированных данных, представленных в виде вариационного ряда, используется взвешенное среднее линейное отклонение, где весами выступают частоты соответствующих вариант:
Дисперсией (s 2) называется средняя арифметическая величина, полученная из квадратов отклонений значений признака от их средней: · для несгруппированных данных:
· для сгруппированных данных:
Квадратный корень из дисперсии называется средним квадратическим отклонением (его называют также стандартным отклонением): · для несгруппированных данных:
· для сгруппированных данных:
Абсолютные показатели вариации, за исключением дисперсии, имеют те же единицы измерения, что и исследуемый показатель вариационного ряда. Поэтому, если экономическая интерпретация, например, среднего линейного отклонения, проста и понятна физически, то в случае с дисперсией она затруднена. Однако дисперсия рассчитывается в статистическом анализе гораздо чаще, чем другие показатели вариации. Связано это с тем, что дисперсия широко используется в таких видах статистического анализа, как корреляционный, регрессионный, дисперсионный, при оценках результатов выборочного наблюдения. Кроме того, именно с помощью дисперсии можно оценить влияние случайных и систематических факторов на формирование значений случайной величины. Для сравнения вариации одного и того же показателя в разных совокупностях (например, заработной платы двух рекламных агентств) или вариации разных показателей в одной совокупности (например, вариации заработной платы и возраста в одном рекламном агентстве) используют относительные показатели вариации. К ним относят: · для сгруппированных данных:
· для сгруппированных данных:
· для сгруппированных данных:
Принято считать, что если значение Vs > 33%, то совокупность неоднородна, и для дальнейшего статистического анализа следует либо исключить крайние значения признака, либо разбить совокупность на однородные группы (требование однородности данных присутствует практически во всех видах статистического анализа). Рассчитаем показатели вариации для приведенных в табл. 7.1 и 7.2 вариационных рядов (табл. 7.3 и 7.4). Расчет абсолютных и относительных
По первому агентству получим следующие данные. Размах вариации: R = x max– x min= 18000 – 4000 = 14000 (руб.). Среднее линейное отклонение (так как ряд сгруппирован и частоты не равны между собой) рассчитываем как взвешенную величину:
Дисперсия:
Среднее квадратическое отклонение:
Коэффициент осцилляции:
Относительное линейное отклонение:
Коэффициент вариации:
Судя по коэффициенту вариации, совокупность по данному признаку можно считать однородной. Проведем расчет аналогичных характеристик вариации по второму агентству (табл. 7.4). Расчет абсолютных и относительных показателей вариации
Показатели вариации по второму агентству: Размах вариации: R = 22 500 – 1500 = 21 000 (руб.); Среднее линейное отклонение:
Дисперсия:
Среднее квадратическое отклонение — 5180 (руб.). Коэффициент осцилляции — 193%. Относительное линейное отклонение — 40%. Коэффициент вариации — 48%. Таким образом, по данному признаку вторая совокупность сотрудников неоднородна. Сравнение относительных показателей вариации по двум совокупностям говорит о том, что дифференциация по уровню заработной платы во втором агентстве гораздо выше, чем в первом, хотя их средние практически совпадают между собой. 6.2. Дисперсия и ее свойства Дисперсия обладает рядом математических свойств. Приведем основные из них: 1) если xi= c, где с — постоянная величина, то дисперсия будет равна нулю; 2) если из всех значений признака вычесть постоянную величину с, то дисперсия от этого не изменится:
3) если все индивидуальные значения признака уменьшить в d раз, то дисперсия уменьшится в d 2 раз:
На приведенных свойствах дисперсии основан один из методов ее расчета — способ моментов. Согласно ему, дисперсию можно вычислить по следующей формуле (применяется только в случае вариационных рядов с равными интервалами):
где с — значение середины интервала, находящегося в центре ряда (если количество интервалов четное, то берется середина интервала из центра ряда с наибольшей частотой); d — величина интервалов;
По данным табл. 7.5 определим дисперсию способом моментов. Расчет дисперсии способом моментов*
* По данным табл. 7.1.
или
Если при расчете дисперсии способом моментов взять за постоянную величину с нуль, а за d — единицу, то приведенная выше формула примет следующий вид:
Таким образом получаем, что дисперсия равна разности между средней из квадратов индивидуальных значений признака и квадрата средней. Применим данный способ расчета дисперсии. Пусть известно, что средняя арифметическая величина, рассчитанная для вариационного ряда, равна 56 дол., а средний квадрат его индивидуальных значений — 3322. Определим дисперсию.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.007 с.) |



 ) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение
) представляет собой среднюю арифметическую величину из абсолютных значений отклонений отдельных значений признака от их средней. Если данные не сгруппированы, то рассчитывается невзвешенное среднее линейное отклонение



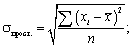
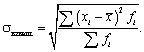
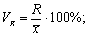







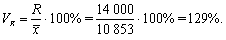



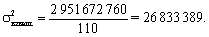



 — момент второго порядка;
— момент второго порядка; — момент первого порядка.
— момент первого порядка. d = 2
d = 2