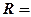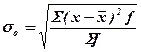Тема. Статистическое изучение вариации

Цель занятия ˗ изучить основные показатели вариации и методику их расчета.

Контрольные вопросы к занятию

Вопрос	Ответ
Что называется вариацией?
Как связаны между собой вариация и типичность средней величины?
На какие группы делятся показатели вариации?
Какие показатели вариации относятся к абсолютным?
Какие показатели вариации относятся к относительным?
В чем назначение показателей вариации?
Какие показатели вариации являются наиболее распространенными?
В чем заключается правило сложения дисперсий?
Какие свойства дисперсии используются для ее расчета по способу моментов?
Как рассчитывается дисперсия альтернативного признака?

 

Задание № 1

Заполните пустые ячейки таблицы.

Показатель вариации	Формула
Для несгруппированных данных	Для сгруппированных данных
Размах вариации
Среднее линейное отклонение
Дисперсия
Среднее квадратическое отклонение
Коэффициент осцилляции
Относительное линейное отклонение
Коэффициент вариации

Задание № 2

Определить степень вариации средней заработной платы в организации, используя абсолютные и относительные показатели.

Средняя ЗП, тыс. руб.	Кол-во рабочих, чел.
3000-4000
4000-5000
5000-6000

Средняя заработная плата по организации, млн. руб.:

Размах вариации:

Среднее линейное отклонение:

 

Дисперсия: σ²=

 

Среднее квадратическое отклонение: σ =

 

Коэффициент осцилляции:

 

Относительное линейное отклонение:

 

Коэффициент вариации: V=

 

 

Задание № 3

Определить степень изменения выработки рабочих в бригаде, используя абсолютные и относительные показатели вариации.

Выработка 1 рабочего, шт.	Кол-во рабочих, чел.

Решение:

 

 

Задание № 4

Определить дисперсию прибыли по группе предприятий всеми известными способами, в т. ч. с использованием её математических свойств.

 

Прибыль, млн. руб.

Кол-во предприятий

до 1000

1000-1500

1500-2000

2000 и более

S

 

Средняя прибыль, млн. руб.:

 

1-й способ:

 

 

2-й способ:

3-й способ:

 

Задание № 5

Определить дисперсию среднемесячной заработной платы работающих по организации всеми известными способами, в т. ч. с использованием её математических свойств.

ЗП, тыс. руб.

Кол-во человек

до 3000

3000-3500

3500-4000

4000 и более

S

Среднемесячная ЗП, тыс. руб.:

 

 

1-й способ:

 

 

2-й способ:

3-й способ:

Задание № 6

Решите примеры.

Задание	Ответ
Чему равен размах вариации? X: 30; 10; 15; 25; 70; 85
Чему равен размах вариации? X: 1; 2,7; 8; 12; 20; 21
Чему равна дисперсия, если среднее квадратическое отклонение равно 5, а среднее значение признака 2?
Чему равно среднее квадратическое отклонение, если дисперсия равна 16, а среднее значение признака 2?
Размах вариации равен 80, средняя величина признака равна 8. Рассчитайте коэффициент осцилляции.
Коэффициент осцилляции равен 8, средняя величина признака равна 4. Рассчитайте размах вариации.
Среднее линейное отклонение равно 25, средняя величина признака равна 5. Рассчитайте относительное линейное отклонение.
Относительное линейное отклонение равно 4, средняя величина признака равна 9. Рассчитайте среднее линейное отклонение.
Чему равен коэффициент осцилляции, если размах вариации равен 5, среднее квадратическое отклонение равно 1, а среднее значение признака 5?
Чему равно относительное линейное отклонение, если среднее линейное отклонение равно 15, дисперсия равна 25, а среднее значение признака 10?
Чему равен коэффициент вариации, если среднее квадратическое отклонение равно 2, а среднее значение признака 10?
Среднее квадратическое отклонение равно 10, средняя величина признака равна 4. Рассчитайте коэффициент вариации.
Коэффициент вариации равен 10, средняя величина признака равна 6. Рассчитайте среднее квадратическое отклонение.
Коэффициент вариации равен 10, средняя величина признака равна 6. Рассчитайте дисперсию.
Дисперсия признака равна 2. Все значения признака увеличились в 2 раза. Чему будет равна дисперсия?
Дисперсия признака была равна 27. Все значения признака уменьшились в 3 раза. Чему будет равна дисперсия?
Если в представленном ряду (Х: 45, 65, 85, 95, 105) все значения признака увеличить на число X0 = 10, как изменится дисперсия?
Если в представленном ряду (Х: 90, 120, 150, 180, 210, 240) все значения признака уменьшить на число X0 =25, как изменится дисперсия?
Если представленные частоты ряда (f=2, 5, 3, 4, 2) увеличить в 2 раза, как изменится дисперсия?
Если представленные частоты ряда (f=2, 4, 8, 10, 6) уменьшить в 2 раза, как изменится дисперсия?

Задание № 7

Имеются следующие данные о товарообороте двух магазинов

Номер магазина	Среднедневной товарооборот, млн. руб.	Дисперсия среднедневного товарооборота	Коэффициент вариации, %

Определить:

1) в каком магазине и на сколько процентов выше товарооборот.

2) в каком магазине выше вариация товарооборота.

Задание № 8

Имеются данные о распределении рабочих двух бригад, работающих по разным технологиям, по уровню производительности труда в млн. руб.

Бригада № 1 (6 чел.):130, 145, 155, 160, 170, 180.

Бригада № 2 (8 чел.): 260, 240, 170, 200, 150, 210, 220, 230.

Определить:

1) средний уровень производительности труда по каждой бригаде;

2) общую дисперсию уровня производительности труда по двум бригадам;

3) внутригрупповые дисперсии производительности труда;

4) межгрупповую дисперсию;

5) проверить правило сложения дисперсий.

 

1. Средний уровень производительности труда:

· по бригаде № 1

 

· по бригаде № 2

 

 

· по двум бригадам

 

2. Общая дисперсия уровня производительности труда по двум бригадам:

 

 

3. Внутригрупповая дисперсия производительности труда:

 

· по бригаде № 1

 

 

· по бригаде № 2

 

Средняя из внутригрупповых дисперсий:

 

 

Производительность труда, млн. руб.
бригада № 1
Итого по бригаде № 1
бригада № 2
Итого по бригаде № 2
Итого по двум бригадам

 

4. Межгрупповая дисперсия

 

Средняя производительность труда по бригаде, млн. руб.	Число рабочих в бригаде, чел.
S

 

 

5. Проверка правила сложения дисперсий:

Задание № 9

1. По результатам проверки качества продукции определено, что 240 единиц соответствуют стандарту, а 30 – не соответствуют. Определить дисперсию доли нестандартной продукции.

2. Зимнюю экзаменационную сессию 20 студентов группы сдали успешно, а 5 имели академическую задолженность. Определить дисперсию доли студентов, успешно сдавших сессию.

 

 

Практическое занятие № 7

Тема. Выборочное наблюдение

 

Цель занятия ˗ освоить методологию проведения выборочного наблюдения и научиться рассчитывать характеристики выборочной совокупности.

Контрольные вопросы к занятию

Вопрос	Ответ
Какой вид наблюдения называется выборочным?
В чем заключается основная цель выборочного наблюдения?
Перечислите правила отбора единиц из генеральной в выборочную совокупность.	·   ·   ·
В чем заключаются преимущества выборочного наблюдения по сравнению со сплошным?
Перечислите основные этапы выборочного наблюдения.	· · · · ·
Что называют ошибками выборочного наблюдения?
Почему ошибки выборочного наблюдения называют средними?
Для чего применяются предельные ошибки выборочного наблюдения?
Что показывает коэффициент доверия t при расчете предельных ошибок выборочного наблюдения?
Какая выборка называется малой?

Задание № 1

Заполните пустые ячейки таблицы.

Характеристики генеральной и выборочной совокупности

Показатели	Совокупность
генеральная	выборочная
	N
Среднее значение признака
		m
Доля единиц, обладающих изучаемым признаком
	1-p (q)
Дисперсия

 

Задание № 2

Заполните пустые ячейки схемы классификации видов, способов и методов отбора единиц в выборочную совокупность.

 

Задание № 3

Соедините стрелками соответствующий метод отбора и его характеристику.

 

 

		Отбор единиц из генеральной совокупности производится в каком-либо механическом порядке
		Отбор из генеральной совокупности не отдельных единиц, а групп, внутри которых проводится сплошное обследование всех единиц
	Серийный
	Комбинированный
		Через определенные промежутки времени происходит фиксация состояния изучаемой совокупности
	Метод моментных наблюдений
		Отбор проводится при помощи жеребьёвки или таблицы случайных чисел

 

Задание № 4

Каждый пятый спортсмен пройдет допинг-контроль

Соедините стрелками соответствующий метод отбора и пример его исполнения.

	Моментных наблюдений
		Мальчики – налево, девочки – направо. 10 % мальчиков и 10 % девочек идут на субботник

Задание № 5

Заполните таблицу для расчета средних ошибок выборки для различных видов и методов отбора.

 

Метод отбора	Вид отбора
Повторный	Бесповторный
Для средней	Для доли	Для средней	Для доли
Случайный и механический
Типический
Серийный

Алгоритм решения задач по расчету ошибки выборочного наблюдения:

1. Определяем, о чем в задаче идет речь – о средней или о доле?

2. Определяем вид и метод отбора.

3. Находим формулу для расчета средней ошибки выборки.

4. Определяем необходимые показатели для расчета средней ошибки.

5. Рассчитываем среднюю ошибку выборки.

6. Рассчитываем предельную ошибку выборки в соответствии с доверительной вероятностью.

7. Рассчитываем пределы нахождения генеральной средней или доли.

 

Задание № 6

Из 20000 изделий для проверки массы методом случайной повторной выборки было отобрано 200 изделий. Средний вес изделия по результатам выборки составил 30 г. Значение среднего квадратичного отклонения составило 4. Необходимо определить:

1) с вероятностью 0,954 определить пределы, в которых находится средний вес изделия в генеральной совокупности;

2) как изменятся пределы, в которых находится средняя по генеральной совокупности, если вероятность будет равна 0,997?

 

Задание № 7

В цеху работает 2450 ткачей. Для определения среднего объема производства ткани в час была организована 4 %-ная случайная бесповторная выборка ткачей. По ее результатам было получено следующее распределение ткачей по выработке ткани в час:

Выработка ткани, пог. м.	Число ткачей
2-6
6-10
10-14
14-18
18-22
22-26

С вероятностью 0,954 найдите пределы, в которых будет находиться средняя выработка ткани в генеральной совокупности.

 

 

Задание № 8

В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2 %-я бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:

Число детей в семье	Количество семей

С вероятностью P=0,954 найти пределы, в которых будет находиться среднее число детей в семье по генеральной совокупности.

 

 

Задание № 9

При контрольной проверке качества электроламп была проведена серийная выборка. Из партии, содержащей 100 коробок с лампами, было выбрано 5 механическим методом. В результате сплошного обследования находящихся в коробках ламп получены данные о проценте бракованных ламп, которые составили соответственно 3 %, 1,05 %, 2,01 %, 4,0 %, 0,6 %. С вероятностью 0,683 найдите средний процент бракованных ламп в партии.

 

Задание № 10

С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек была проведена 25 %-ная механическая выборка. По результатам наблюдения оказалось, что у 10 % обследованных потери рабочего времени достигали более 45 минут в день. С вероятностью 0,997 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 минут в день.

 

Задание № 11

С целью определения среднего размера вклада в отделениях сбербанка города предполагается провести механическую бесповторную выборку лицевых счетов из общего их числа 67800. По данным предыдущего обследования установлено, что среднее квадратическое отклонение размера вклада равно 14000 рублей. С вероятностью 0,997 определите необходимый объём выборочной совокупности при условии, что ошибка выборки не должна превышать 1000 рублей.

 

 

Задание № 12

В ОАО «Омега» 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Дисперсия доли рабочих, имеющих профессиональные заболевания по результатам пробного обследования, равна 225. С вероятностью 0,954 рассчитайте необходимое для выборки количество бригад, если ошибка выборки не должна превышать 5 %.

 

 

Задание № 13

С целью определения средних затрат времени при поездках на работу населения города численностью 350000 человек планируется провести выборочное наблюдение на основе случайного повторного отбора. Сколько людей должно быть обследовано, чтобы с вероятностью 0,954 ошибка выборочной средней не превышала 1 минуту при среднем квадратическом отклонении 15 минут.

 

 

Практическое занятие № 8