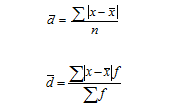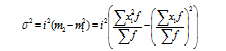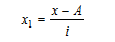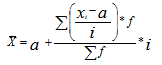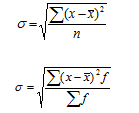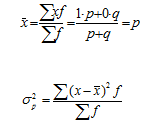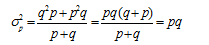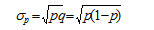Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет моды и медианы в интервальном вариационном рядуСодержание книги
Поиск на нашем сайте
Описательный характер моды и медианы связан с тем, что в них не погашаются индивидуальные отклонения. Они всегда соответствуют определенной варианте. Поэтому мода и медиана не требуют для своего нахождения расчетов, если известны все значения признака. Однако в интервальном вариационном ряду для нахождения приближенного значения моды и медианы в пределах определенного интервала прибегают к расчетам. Для расчета определенного значения модальной величины признака, заключенного в интервале, применяют формулу: Мо = ХМо + iМо *(fМо – fМо-1)/((fМо – fМо-1) + (fМо – fМо+1)), Где ХМо – минимальная граница модального интервала; iМо – величина модального интервала; fМо – частота модального интервала; fМо-1 – частота интервала, предшествующего модальному; fМо+1 – частота интервала, следующего за модальным. Покажем расчет моды на примере, приведенном в таблице 2. Таблица 2. Распределение рабочих предприятия по выполнению норм выработки
Чтобы найти моду, первоначально определим модальный интервал данного ряда. Из примера видно, что наибольшая частота соответствует интервалу, где варианта лежит в пределах от 100 до 105. Это и есть модальный интервал. Величина модального интервала равна 5. Подставляя числовые значения из таблицы 2. в указанную выше формулу, получим: Мо = 100 + 5 * (104 -12)/((104 – 12) + (104 – 98)) = 108,8 Смысл этой формулы заключается в следующем: величину той части модального интервала, которую нужно добавить к его минимальной границе, определяют в зависимости от величины частот предшествующего и последующего интервалов. В данном случае к 100 прибавляем 8,8, т.е. больше половины интервала, потому что частота предшествующего интервала меньше частоты последующего интервала. Исчислим теперь медиану. Для нахождения медианы в интервальном вариационном ряду определяем сначала интервал, в котором она находится (медианный интервал). Таким интервалом будет такой, комулятивная частота которого равна или превышает половину суммы частот. Комулятивные частоты образуются путем постепенного суммирования частот, начиная от интервала с наименьшим значением признака. Половина суммы частот у нас равна 250 (500:2). Следовательно, согласно таблицы 3. медианным интервалом будет интервал со значением заработной платы от 350000 руб. до 400000 руб.
Таблица 3. Расчет медианы в интервальном вариационном ряду
До этого интервала сумма накопленных частот составила 160. Следовательно, чтобы получить значение медианы, необходимо прибавить еще 90 единиц (250 – 160). При определении значения медианы предполагают, что значение единиц в границах интервала распределяется равномерно. Следовательно, если 115 единиц, находящихся в этом интервале, распределяются равномерно в интервале, равном 50, то 90 единицам будет соответствовать следующая его величина: 50 * 90/115 = 39,1 Прибавив полученную величину к минимальной границе медианного интервала, получим искомое значение медианы: Ме = 350 +39,1 = 389,1 тыс. руб. Формула исчисления медианы для интервального вариационного ряда имеет следующий вид: Ме = ХМе + iМе * (∑f/2 – SМе-1)/fМе, Где ХМе – начальное значение медианного интервала; iМе – величина медианного интервала; ∑f – сумма частот ряда (численность ряда); SМе-1 – сумма накопленных частот в интервалах, предшествующих медианному; fМе – частота медианного интервала. Подставляя в эту формулу значения из примера, приведенного выше, получим значение медианы: Ме = 350 + 50 * (500/2 – 160)/115 = 389,1 тыс. руб. Следовательно, в наших примерах мода равна 108,8, а медиана – 389,1.
Вопрос 23 Эмпирические моменты Знание моментов распределения также многое может сказать о его виде и свойствах. Введем эмпирические (выборочные) аналоги неизвестных теоретических (истинных) моментов распределения. Пусть
среднее, дисперсия,
Коротко определить содержание правого и левого столбцов таблицы можно так: неизвестное "среднее по пространству" заменяется "средним по времени"
Вопрос 24 Показатели вариации Вариация – различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. К показателям вариации относятся: I группа – абсолютные показатели вариации размах вариации среднее линейное отклонение дисперсия среднее квадратическое отклонение II группа – относительные показатели вариации коэффициент вариации коэффициент осцилляции относительное линейное отклонение Самым элементарным показателем вариации признака является размах вариации R. Размах вариации показывает лишь крайние (min, max) отклонения признака от общей средней.
Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику. Среднее линейное отклонение – средняя арифметическая абсолютных значений отклонений (модуль отклонений) отдельных вариантов от их средней арифметической: для несгруппированных данных (простое) для сгруппированных данных (взвешенное)
Дисперсия признака – средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий: Простая дисперсия для несгруппированных данных Взвешенная дисперсия для вариационного ряда
Cвойства дисперсии: если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А- дисперсия не изменится; если все значения признака уменьшить или увеличить в одно и то же число раз (k раз), то дисперсия уменьшится или увеличится в k 2 раз. Используя второе свойство дисперсии, можно получить формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
где i – величина интервала, X 1 – новые (преобразованные) значения вариантов (А – условное начало, в качестве которого удобно использовать середину интервала или величину признака, обладающего наибольшей частотой.
Момент второго порядка Квадрат момента первого порядка
Среднее квадратическое отклонение равно корню квадратному из дисперсии: для несгруппированных данных (простое) для вариационного ряда по сгруппированным данным (взвешенное) Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются отдельные варианты от их среднего значения.
Среднее значение альтернативного признака и его дисперсия: Среднее значение альтернативного признака Дисперсия альтернативного признака
Подставив в формулу дисперсии q = 1 – p, получим:
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком и доли единиц, не обладающих данным признаком. Среднее квадратическое отклонение альтернативного признака:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.151.112 (0.006 с.) |

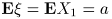 ,
,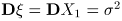 ,
,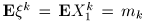 - теоретические
- теоретические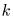 -й момент. Хорошо известны их выборочные "двойники":
-й момент. Хорошо известны их выборочные "двойники": - выборочное среднее
- выборочное среднее
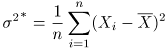 - выборочная дисперсия
- выборочная дисперсия
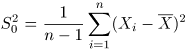 - несмещенная выборочная дисперсия
- несмещенная выборочная дисперсия