Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типичные величины высшего порядка дискретной случайной переменной (моменты)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Моменты. Кроме первого и второго моментов, при описании случайных величин иногда используются и другие моменты: третий, четвертый и т.д. Мы дадим их определения отдельно для дискретных и для непрерывных случайных величин. Определение. Для дискретной случайной величины ξ со значениями x1, x2,..., имеющих вероятности p1, p2,..., k _ым моментом Mξk называется величина Mξk = Чтобы приведенные формулы имели смысл, требуется, чтобы суммы и интегралы сходились абсолютно. Так же, как математическое ожидание и дисперсия, моменты существуют не для всех случайных величин. Определение типичных величин непрерывной случайной переменной. Типичные величины положения. Биномиальное распределение Биномиальное распределение — дискретное распределение вероятностей случайной величины
Гипергеометрическое распределение. Гипергеометрическое распределение — это дискретное вероятностное распределение, которое описывает количество успехов в выборке без возвращений длины n над конечной совокупностью объектов. Это выборка из N объектов, из которых m дефектных. Гипергеометрическое распределение описывает вероятность того, что именно k дефектных в выборке из n конкретных объектов, взятых из совокупности. Если случайная величина распределена гипергеометрически с параметрами N, m, n тогда вероятность получить ровно k успехов (дефектных объектов в предыдущем примере) будет следующей:
Распределение Пуассона Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Распределение Пуассона — это частный случай биномиального распределения. Из математики известна формула, позволяющая примерно подсчитать значение любого члена биномиального распределения:
Нормальное распределение Нормальное распределение, также называемое гауссовым распределением, гауссианой или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
· отклонение при стрельбе · некоторые погрешности измерений (однако, многие погрешности приборов в технике имеют сильно не нормальные распределения) · рост живых организмов Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный). Плотность вероятности Функция распределения
Закон распределения хи-квадрат. Распределение
Распределение Стьюдента Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.
Распределение Парето. Распределе́ние Паре́то в теории вероятностей — двухпараметрическое семейство абсолютно непрерывных распределений, являющихся степенными. Называется по имени Вилфредо Парето.
Плотность вероятности Функция распределения
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 661; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

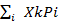 , а k _ым центральным моментом называется величина
, а k _ым центральным моментом называется величина 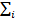 (xi − Mξ)kpi. Для непрерывной случайной величины с плотностью p(x), k _ым моментом называется величина
(xi − Mξ)kpi. Для непрерывной случайной величины с плотностью p(x), k _ым моментом называется величина 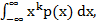 , а k _ым центральным моментом называется величина M(ξ − Mξ)k =
, а k _ым центральным моментом называется величина M(ξ − Mξ)k = 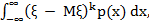
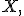 принимающей целочисленные значения
принимающей целочисленные значения  с вероятностями:
с вероятностями:  Данное распределение характеризуется двумя параметрами: целым числом n>0 называемым числом испытаний, и вещественным числом p, 0 ≤ p ≤ 1 называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из n независимых испытаний, в каждом из которых может произойти "успех" с вероятностью p, то случайная величина, равная числу успехов во всей серии, имеет указанное распределение.
Данное распределение характеризуется двумя параметрами: целым числом n>0 называемым числом испытаний, и вещественным числом p, 0 ≤ p ≤ 1 называемом вероятностью успеха в одном испытании. Биномиальное распределение — одно из основных распределений вероятностей, связанных с последовательностью независимых испытаний. Если проводится серия из n независимых испытаний, в каждом из которых может произойти "успех" с вероятностью p, то случайная величина, равная числу успехов во всей серии, имеет указанное распределение.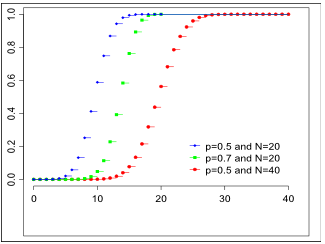 Функция вероятности Функция распределения
Функция вероятности Функция распределения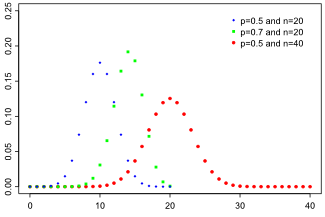
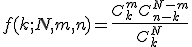 .
.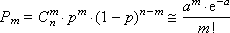 .
.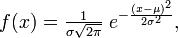 где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия. Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия. Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

 (хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
(хи-квадрат) с k степенями свободы — это распределение суммы квадратов k независимых стандартных нормальных случайных величин.
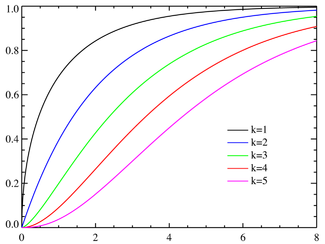 Плотность вероятности Функция распределения
Плотность вероятности Функция распределения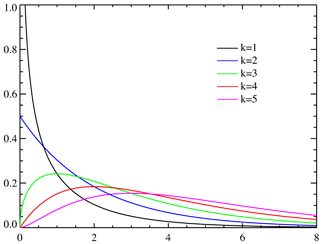

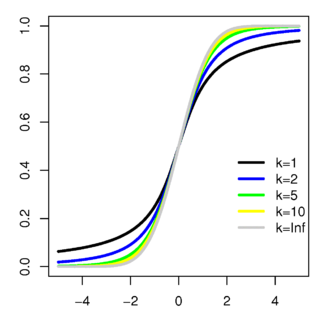 Плотность вероятности
Плотность вероятности 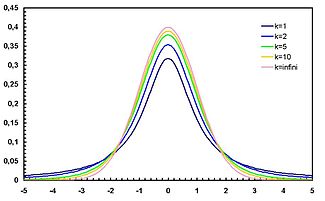 Функция распределения
Функция распределения