
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многомерные случайные величиныСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Многомерной случайной величиной называют совокупность случайных величин, определенных на одном и том же пространстве элементарных событий. Она задается несколькими числами, рассматриваемыми совместно. Многомерные случайные величины могут быть дискретными, непрерывными и смешанными. Двумерная дискретная случайная величина (X, У) задается таблицей распределения, как совокупность пар значений (Х = хi, У = уj) и соответствующих им вероятностей
Условные вероятности
Многомерные случайные величины задаются функциями распределения.
Для характеристики двумерной случайной величины используют математические ожидания, дисперсии и средние квадратические отклонения составляющих Х и У, а также корреляционный момент (ковариацию) cov(x,y) и коэффициент корреляции (r)
Для дискретных случайных величин Х, У:
Для непрерывных случайных величин Х, У:
Коэффициент корреляции случайных величин Х и У:
1 В группе 8 мужчин и 5 женщин. Наугад отбирается 2 человека из группы. Составить совместный закон распределения случайных величин (Х, У), где Х – случайная величина, отобран мужчина, У – отобрана женщина. Определить коэффициент корреляции между Х и У. 2 В первой группе 8 мужчин, из которых 5 занимаются спортом, во второй 6 женщин, из которых две занимаются спортом. Из каждой группы случайно отобрано по одному человеку. Составить совместное распределение случайных величин (Х, У), где Х – отобранный из первой группы мужчина занимается спортом, У – отобранная из второй группы женщина занимается спортом. Зависимы ли случайные величины Х и У? 3 Задана двумерная дискретная случайная величина ХУ: а) б)
Определить: а) законы распределения составляющих случайных величин; б) математическое ожидание, дисперсию и среднее квадратическое отклонение составляющих Х и У; в) условный закон распределения случайной величины У, если Х = 2; г) условный закон распределения случайной величины Х, если У = 5. 4 Задана двумерная дискретная случайная величина ХУ: а) б)
Определить: а) законы распределения составляющих; б) математическое ожидание, дисперсию и среднее квадратическое отклонение составляющих случайных величин Х и У; 5 Задана функция распределения двумерной случайной величины
Определить: а) двумерную плотность вероятностей системы (Х, У); б) вероятность попадания случайной точки (Х, У) в прямоугольник, ограниченный прямыми х = 0, х = 2, у = 1, у = 3. 6 Найти вероятность попадания случайной точки (Х, У) в прямоугольник, ограниченный прямыми х = 1, х = 2, у = 3, у = 5, если известна функция распределения:
7 Задана функция распределения двумерной случайной величины:
Найти двумерную плотность вероятности системы (Х, У). 8 Имеется распределение хозяйств по дозам внесения удобрений и урожайности озимой пшеницы:
Найти безусловные и условные законы распределения случайных величин урожайности (Х) и доз внесения удобрений (У), (а – число по указанию преподавателя). 9 Система случайных величин (Х, У) подчинена закону распределения с плотностью
Определить: а) коэффициент а; б) М(Х), М(У); в) Д(Х), Д(У). 10 Плотность совместного распределения непрерывной двумерной случайной величины 11 Непрерывная двумерная случайная величина (Х,У) распределена равномерно внутри треугольника с вершинами О (0,0), А (0,6) и В (6,0). Найти: а) двумерную плотность вероятности системы; б) плотности и условные плотности составляющих систем. 12 Система случайных величин (Х,У) распределена равномерно внутри квадрата со стороной а, диагонали которого совпадают с осями координат. Найти: а) двумерную плотность вероятности системы; б) плотности и условные плотности составляющих системы. 13 Задана плотность совместного распределения непрерывной двумерной случайной величины (Х,У):
Найти математические ожидания и дисперсии составляющих. 14 Система случайных величин (Х,У) равномерно распределена в треугольнике, ограниченном прямыми х=0, у=0, х+у=а (а>0). Определить: а) математические ожидания и дисперсии случайных величин Х и У, б) корреляционный момент. 15 Заданы плотности распределения независимых составляющих непрерывной случайной величины (Х,У):
Найти: а) плотность совместного распределения системы; б) функцию распределения системы. 16 Доказать, что если Х и У связаны линейной зависимостью, то абсолютная величина коэффициента корреляции равна 1.
Цепи Маркова
Результаты различных экспериментов или испытаний могут быть представлены в виде определенной последовательности букв или цифр, которые рассматриваются как процессы перехода от одного состояния в другое. Можно оценить вероятность такого перехода. Модель случайного процесса объединяет множество состояний и множество вероятностей перехода из одного состояния в другое. Множество (пространство) состояний может быть конечным и бесконечным. Последовательность состояний образует цепь Маркова, если в отдельном испытании система принимает одно из возможных состояний, не зависящее от результатов ранее произведенных испытаний. Вероятность
Вероятность перехода процесса из состояния S
Аналогично получается матрица перехода за три шага
1 Вероятности перехода за один шаг в цепи Маркова задаются матрицей: а) Найти число состояний системы. Построить граф, соответствующий матрице р. 2 Задана матрица вероятностей переходов
Каковы пределы изменений р и S? 3 В урне имеется 5 белых и черных шаров. Из урны случайно извлекается один шар, а обратно в урну возвращается один шар другого цвета. Опыт повто ряется неоднократно. Найти матрицу переходных вероятностей, состояниями которой является количество белых шаров в урне. Найти вероятности перехода за два шага. 4 Игральная кость перекладывается многократно с равной вероятностью случайным образом с одной грани на любую из соседних четырех граней, независимо от исхода предыдущего испытания. К какому пределу стремится при 5 Имеется пять стульев, расположенных один возле другого. Человек пересаживается с одного стула на рядом стоящий, причем эти перемещения определяются бросанием правильной игральной кости. Стулья обозначены буквами А,В,С,Д,Е. Вначале он сидит на среднем стуле С. Если человек сидит на крайнем стуле, то: возвращается на стул С, когда выпадет четное число очков; остается на том же месте при выпадении нечетного числа очков. Если он сидит не на крайнем стуле, то: перемещается налево при выпадении одного или двух очков; перемещается направо при выпадении трех или четырех очков; остается на том же месте при выпадении пяти или шести очков. Найти: а) матрицу вероятностей переходов за один шаг; б) вероятности следующих последовательностей: С,Д,Е,С,Д,А,С; С,В,Д,Е,Е,А; С,В,А,А,С,Д; С,Д,Е,С,Е,С; А,А,С,Д,Е,Е. 6 Студент, для получения профессионального образования, обучается в колледже в течение трех лет. Ежегодно он сдает комплексный экзамен. Если студент успешно сдаст экзамен, то он переводится на следующий курс или заканчивает колледж с дипломом специалиста. Если студент экзамен не сдает, то он остается на соответствующем курсе второй год. Вероятность успешной сдачи экзамена на первом году обучения составляет 0,7; втором – 0,8; третьем – 0,9. Указать подходящее число состояний системы. Найти матрицу вероятностей перехода за один шаг для ежегодных передвижений студента по курсам (первый, второй, третий год обучения, окончание колледжа). Определить вероятность, что студент будет обучаться на третьем курсе после сдачи второго экзамена. Определить среднее число лет, которые студент проводит в колледже.
ВАРИАЦИОННЫЕ РЯДЫ Ряд значений (вариант) признака, расположенных в порядке возрастания или убывания с соответствующими им весами (частотами или частостями), называется вариационными рядом (рядом распределения). Частота (ni) показывает, сколько раз встречается тот или иной вариант (значение признака) в статистической совокупности. Частость или относительная частота (wi) показывает, какая часть единиц совокупности принимает определенное значение или из интервала значений. В дискретных рядах перечисляются возможные значения признака
Дискретный ряд распределения можно изобразить графически в виде полигона распределения частот или частостей. В этом случае по оси абсцисс откладывают значения признака, а по оси ординат Интервальные ряды изображают в виде гистограммы – фигуры, состоящей из прямоугольников. По оси абсцисс откладываются значения признака (границы интервалов), по оси ординат – частоты или частости. Дискретные и интервальные ряды можно графически представить в виде кумуляты или огивы. При построении кумуляты, в отличии от полигона, по оси ординат откладываются накопленные частоты или частости. При построении огивы на оси абсцисс наносятся точки, соответствующие накопленным частотам или частостям, а по оси ординат значения признака. Основной числовой характеристикой вариационного ряда является средняя арифметическая:
Модой вариационного ряда называется значение признака, которое имеет наибольшую частоту. Медиана – значение признака у той единицы совокупности, которая делит вариационный ряд пополам. В интервальных вариационных рядах с равным интервалами, мода и медиана определяется по следующим формулам:
где h- величина интервалов;
Характеристики вариационного ряда могут быть рассчитаны с помощью моментов распределения. Моментом распределения k-го порядка называется средняя арифметическая k-ых степеней отклонений значений признака от определенной величины С.
Обычно к = 0,1,2,3,4. Если С = 0, то момент называется начальным
Если С =
Центральные моменты можно рассчитать через начальные, используя формулы:
В качестве меры симметричности ряда распределения применяется коэффициент асимметрии:
где Если если если Мерой крутости (островершинности) ряда распределения является эксцесс: где m4 – центральный момент четвертого порядка. Если Э если Э < 0, то распределение островершинное; если Э > 0, то распределение плосковершинное. Колеблемость признака характеризуется с помощью показателей вариации, к которым относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение. Дисперсия:
Среднее квадратичное отклонение: Коэффициент вариации: Если V > 33%, то считается, что совокупность может быть статистически неоднородной в отношении данного признака.
1 По списку на предприятии числится 100 рабочих, которые имеют следующие разряды: 1,5,2,4,3,4,6,4,5,1,2,2,3,4,5,3,4,5,2,1,4,5,5,4,3,4,6,1,2,4,4,3,5,6,4,3,3,1,3,4,3,1,2,4,4,5,6,1,3,4,5,3,4,4,3,2,6,1,2,4,5,3,3,2,3,6,4,3,4,5,4,3,3,2,6,3,3,4,5,4,4,3,3,2,1,2,1,6,5,4,3,2,3,4,4,3,5,6,1,5. Составить ряд распределения рабочих по разрядам. Найти накопленные частоты и частости. Вариационный ряд изобразить графически. Определить средний разряд рабочего, модальный и медианный разряд, дисперсию и среднее квадратическое отклонение. 2 Имеются следующие данные о числе производственных рабочих в каждом из 100 крестьянских (фермерских) хозяйств: 2,4,5,3,4,6,7,4,5,3,3,4,2,6,5,4,7,2,3,4,4,5,4,3,4,6,6,5,2,3,4,3,5,6,7,2,4,3,4,5,4,6,7,2,5,3,5,4,3,7,2,4,3,4,5,4,3,2,6,7,6,4,3,2,3,4,5,4,3,5,4,3,2,6,4,5,7,5,4,3,4,5,7,4,3,4,5,6,5,3,4,2,2,4,3,7,5,6,4,5. Составить ряд распределения крестьянских (фермерских) хозяйств по числу производственных рабочих на одно хозяйство. Найти накопленные частоты и частости. Вариационный ряд изобразить графически. Определить среднее число производственных рабочих на одно хозяйство, модальное и медианное значения числа рабочих, дисперсию, среднее квадратическое отклонение и коэффициент вариации.. 3 По данным приложения 4 по одному из следующих показателей составить интервальный вариационный ряд с равными интервалами: 1) площадь сельскохозяйственных угодий, га; 2) материальные затраты, млн. руб.; 3) среднегодовая численность работников, чел.; 4) энергетические мощности, л.с.; 5) затраты на производство продукции, млн. руб.; 6) затраты на реализованную продукцию, млн. руб.; 7) среднегодовая стоимость основных фондов, млн. руб.; 8) валовая продукция млн. руб.; 9) реализованная продукция, млн. руб.; 10) затраты по оплате труда, млн. руб.; 11) валовой доход, млн. руб.; 12) прибыль от реализации продукции, млн. руб.; 13) среднегодовая численность работников на 100 га сельхозугодий, чел.; 14) основные фонды на 100 га сельхозугодий, млн. руб.; 15) энергетические мощности на среднегодового работника, л.с.; 16) прибыль на 100 га сельхозугодий, млн.руб.;17) затраты на производство на 100 га сельхозугодий, млн. руб.; 18) материальные затраты на 100 га сельхозугодий, млн.руб.; 19) затраты на реализованную продукцию на 100 га сельхозугодий, млн. руб.; 20) затраты по оплате труда на 100 га сельхозугодий млн. руб.; 21) энергетические мощности на 100 га сельхозугодий, л.с.; 22) валовая продукция сельского хозяйства на 100 га сельхозугодий, млн. руб.; 23) основные фонды на среднегодового работника, тыс. руб.; 24) валовая продукция сельского хозяйства на среднегодового работника, тыс. руб.; 25) реализованная продукция на 100 га сельхозугодий, млн. руб.; 26) затраты по оплате труда на среднегодового работника, тыс. руб.; 27) реализованная продукция на среднегодового работника, тыс. руб.; 28) затраты на реализованную продукцию на 100 га сельхозугодий, млн. руб.; 29) площадь сельскохозяйственных угодий на среднегодового работника, га.; 30) валовой доход на 100 га сельскохозяйственных угодий, млн. руб. Найти накопленные частоты и частости. Ряд распределения изобразить графически. Определить моду, медиану, среднее значение, дисперсию, среднее квадратическое отклонение, коэффициент асимметрии и эксцесс. Сделать выводы по результатам расчетов. 4 Определить абсолютную и относительную плотность распределения работников предприятия по стажу их работы на данном предприятии.
Таблица 1- Распределение работников по стажу работы
Найти средний стаж работы, среднее квадратическое отклонение и коэффициент вариации. 5 Путем устного опроса изучалось качество продукции, выпускаемой фирмой и реализуемой в магазине этой фирмы. Посетители давали оценку качества по десятибалльной шкале.
Таблица 2- Бальная оценка продукции предприятия
Определить средний балл качества продукции, среднее квадратическое отклонение, коэффициент вариации, показатели асимметрии и эксцесса. 6 Имеются следующие данные о площади посева овощей в хозяйствах по совокупности районов. Таблица 3 - Площадь посева овощей на хозяйство, га
Дать сравнительную оценку колеблемости площади посева овощей в хозяйствах двух районов. 7 По данным распределения студентов по результатам сдачи экзаменов определить: а) средний балл успеваемости студентов по каждому предмету и по всем предметам; б) дисперсии балла успеваемости по предмету и в целом по всем предметам; в) межгрупповую дисперсию. Найти общую дисперсию успеваемости, используя правило сложения дисперсий.
Таблица 4 - Распределение студентов группы по результатам сдачи экзаменов
8 Работники предприятия сгруппированы по возрасту.
Таблица 5 - Распределение работников предприятия по возрасту
Определить: а) средний возраст работников предприятия в целом и по категориям: б) модальное и медианное значения возраста работников по категориям и предприятию; в) дисперсию и среднее квадратическое отклонение возраста по категориям работников и предприятию; г) межгрупповую дисперсию возраста работников. Найти общую дисперсию возраста работников, используя правило сложения дисперсий.
ВЫБОРОЧНЫЙ МЕТОД Выборочным называется наблюдение, при котором обследованию подвергается часть единиц совокупности, отобранных на основе научно разработанных принципов, а показатели, найденные по отобранной части единиц, должны достаточно точно характеризовать всю совокупность единиц. Совокупность единиц, из которой производится отбор, называется генеральной совокупностью, а ее часть, подвергающаяся изучению Генеральная доля Отбор единиц производится случайным, механическим, типическим, серийным, комбинированным и другими способами. Случайным называется отбор единиц из генеральной в выборочную совокупность, при котором каждая единица имеет одинаковую вероятность попасть в выборку. Основной задачей выборочного метода является количественная оценка параметров генеральной совокупности по данным выборки. Для того, чтобы статистические оценки давали «хорошие» приближения оцениваемых параметров генеральной совокупности по выборке, они должны обладать свойствами несмещенности, эффективности и состоятельности. Оценка параметров генеральной совокупности может быть точечной и интервальной. Точечная оценка задается одним числом. Оценка, задаваемая двумя числами (границами интервала), называется интервальной. Доверительный интервал рассчитывается по формуле:
для доли для средней где
Таблица 6 - Формулы расчета предельной ошибки выборки при случайном отборе
В больших выборках (n > 60) t находится по таблице значений функций Ф (х) при заданном уровне доверительной вероятности В малых выборках
Таблица 7 - Формулы расчета необходимой численности выборки при случайном отборе
1 Для определения потерь зерна при уборке случайным способом проведено 100 измерений. Средняя величина потерь составила 1,8 ц с одного гектара посевов, при среднем квадратическом отклонении 0,5 ц с га. С доверительной вероятностью 0,95 определить границы, в которых будет находиться средняя величина потерь зерна с 1 га и возможная величина потерь, если площадь уборки зерновых составила 640 га. 2 С помощью случайной выборки изучалось время выполнения производственной операции рабочими бригады. На основании 60 наблюдений установлено, что в среднем на выполнение производственной операции затрачивалось 0,5 часа, при среднем квадратическом отклонении 0,12часа. Считая время выполнения производственной операции нормально - распределенной случайной величиной, определить границы, в которых находится среднее время выполнения производственной операции всех рабочих с доверительной вероятностью: а) 0,9; б) 0,95. 3 Случайным бесповторным способом изучались остатки горюче-смазочных материалов на складе предприятий. Обследовано 110 предприятий из 750. Средние остатки составили 150 т, при среднем квадратическом отклонении 42 т. С доверительной вероятностью 0,95 определить границы, в которых будут находиться средние остатки горюче-смазочных материалов на одно предприятие и общие остатки горюче-смазочных материалов. 4 Считая данные задачи 1 темы 11 результатом 20% выборки, определить: а) несмещенные оценки математического ожидания, дисперсии и среднего квадратического отклонения разряда рабочих; б) доверительный интервал для математического ожидания с доверительной вероятностью 0,95; в) вероятность того, что интервал (0,95 5 Считая данные задачи 2 темы 11 результатом 20% выборки, определить: а) несмещенные оценки математического ожидания, дисперсии и среднего квадратического отклонения числа производственных рабочих в расчете на одно крестьянское (фермерское) хозяйство; б) доверительный интервал для математического ожидания с доверительной вероятностью 0,9; в) объем выборки, при котором с доверительной вероятностью 0,9 предельная ошибка выборки уменьшится в 2 раза, при сохранении значений остальных характеристик. 6 Считая данные задачи 3 темы 11 результатом 20% случайной бесповторной выборки, определить: а) несмещенные оценки математического ожидания, дисперсии и среднего квадратического отклонения изучаемого параметра; б) доверительный интервал для математического ожидания с доверительной вероятностью 0,95; в) вероятность того, что интервал (0,95 7 В районе имеется 10000 дачных участков населения. В результате выборочного обследования 300 дачных участков оказалось, что средняя выборочная урожайность овощей составила 250 ц с гектара при среднем квадратическом отклонении 60 ц с га. Известно, что 40% общей площади посевов овощей занимали помидоры. С доверительной вероятностью 0,95 определить границы, в которых будет находиться средняя урожайность овощей на всех дачных участках и удельный вес посевов помидор. Сколько необходимо обследовать дачных участков, чтобы предельная ошибка выборки по признакам уменьшилась в 1,5 раза? 8 Для определения влажности зерна случайным способом было взято 25 проб. Средний процент влажности зерна составил 16%, а выборочное среднее квадратическое отклонение 2,5%. Определить: а) несмещенные оценки математического ожидания, дисперсии и среднего квадратического отклонения; б) интервал, который покроет математическое ожидание с доверительной вероятностью, 0,95. 9 Вероятность изготовления продукции высшего качества фирмой составляет 0,9. Сколько необходимо обследовать единиц продукции, чтобы с доверительной вероятностью 0,95 можно было утверждать, что доля продукции высшего качества по выборке будет отклоняться от постоянной вероятности по модулю не более чем на 0,03? 10 Случайным бесповторным способом проведено выборочное обследование семей района. Из 1300 семей обследовано 130, по которым определен душевой доход на члена семьи, представленный в виде интервального вариационного ряда. Таблица 8 - Распределение семей по величине месячного дохода на одного члена семьи
С доверительной вероятностью 0,95 определить границы, в которых будет находиться средний месячный доход на одного члена семьи по району, а также доля семей с доходами менее 8,0 тыс. руб. на одного члена семьи. 11 В фирме проведен выборочный опрос 10% работников по вопросам изменения условий труда. Из 90 работников основного производства за изменение условий труда высказалось 65 человек, из 30 работников вспомогательного производства – 20, а из 25 работников, занятых управлением фирмой – 21. С доверительной вероятностью 0,95 определить границы, в которых будет находиться доля работников фирмы, поддерживающих изменение условий труда. 12 Для определения влияния микроэлементов на результаты откорма свиней проведен опыт на 8 группах животных. Рационы отличаются набором и дозами микроэлементов.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.62 (0.035 с.) |

 ,
,  .
. ,
,  ,
,  ,
, . (9.1)
. (9.1)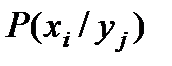 и
и  находятся по формулам:
находятся по формулам: . (9.2)
. (9.2) , (9.3)
, (9.3) ,
,  ,
, (9.4)
(9.4) , (9.5)
, (9.5) . (9.10)
. (9.10) .(9.11)
.(9.11) . (9.12)
. (9.12) . (9.13)
. (9.13)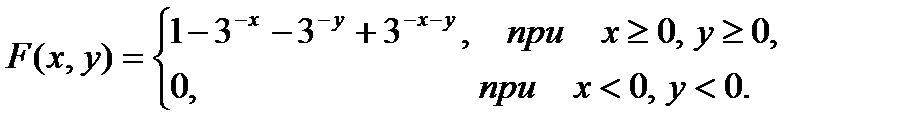

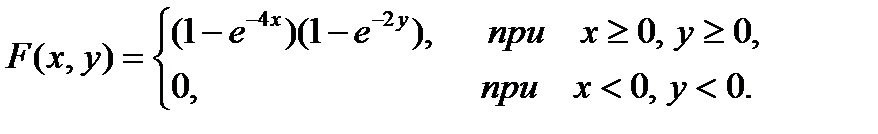
 в квадрате
в квадрате 
 и
и вне квадрата.
вне квадрата. в квадрате
в квадрате 
 и
и  вне квадрата. Доказать, что составляющие Х и У независимы.
вне квадрата. Доказать, что составляющие Х и У независимы.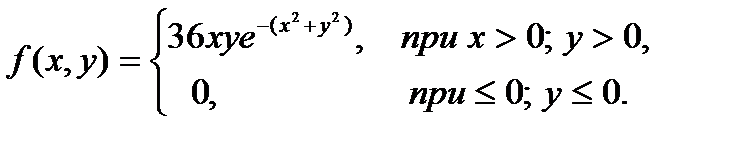

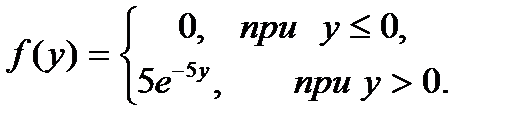
 , есть условная вероятность перехода случайного процесса из состояния Si в состояние
, есть условная вероятность перехода случайного процесса из состояния Si в состояние  за один шаг. Так как она не зависит от номера испытания, то может обозначаться через
за один шаг. Так как она не зависит от номера испытания, то может обозначаться через  . Первый индекс указывает номер предшествующего, а второй – последующего состояния. Если известны вероятности для любой пары состояния, то они могут быть представлены квадратной матрицей перехода.
. Первый индекс указывает номер предшествующего, а второй – последующего состояния. Если известны вероятности для любой пары состояния, то они могут быть представлены квадратной матрицей перехода. , где
, где 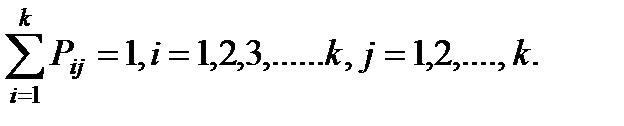 (10.1)
(10.1) в состояние S
в состояние S  за n шагов обозначается
за n шагов обозначается  , а квадратная матрица всех этих вероятностей обозначается
, а квадратная матрица всех этих вероятностей обозначается  . Вероятность перехода процесса из состояния i в состояние j за два шага вычисляется по формуле полной вероятности.
. Вероятность перехода процесса из состояния i в состояние j за два шага вычисляется по формуле полной вероятности.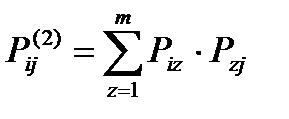 или в матричной записи
или в матричной записи 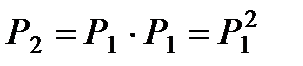 . (10.2)
. (10.2)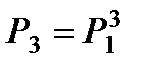 и за n – шагов
и за n – шагов  . (10.3)
. (10.3) б)
б)  .
.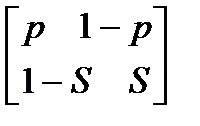
 вероятность того, что в момент времени t игральная кость лежит на грани «5», если в момент времени t=0, она находится в этом же положении?
вероятность того, что в момент времени t игральная кость лежит на грани «5», если в момент времени t=0, она находится в этом же положении? . Если признак непрерывный или число значений дискретного признака велико, то строят интервальный ряд распределения, в котором значения признака задаются в виде интервалов. При построении интервального ряда распределения число интервалов можно определить по формуле Стэрджесса: k=1+3,322 lg n, где n – число единиц совокупности. Величина интервала (h) определяется по формуле
. Если признак непрерывный или число значений дискретного признака велико, то строят интервальный ряд распределения, в котором значения признака задаются в виде интервалов. При построении интервального ряда распределения число интервалов можно определить по формуле Стэрджесса: k=1+3,322 lg n, где n – число единиц совокупности. Величина интервала (h) определяется по формуле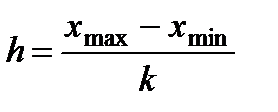 (8.1)
(8.1) соответствующие им частоты или частости. Полученные точки соединяются отрезками.
соответствующие им частоты или частости. Полученные точки соединяются отрезками.
 (8.2)
(8.2)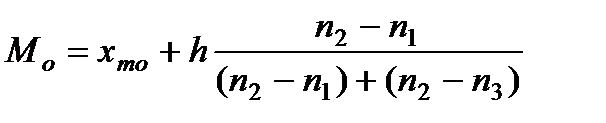 ; (8.3)
; (8.3) (8.4)
(8.4)
 - нижняя граница модального и медиального интервалов;
- нижняя граница модального и медиального интервалов; соответственно частота предмодального, модального и послемодального интервалов;
соответственно частота предмодального, модального и послемодального интервалов; накопленная частота интервала, предшествующего медианному интервалу.
накопленная частота интервала, предшествующего медианному интервалу. (8.5)
(8.5) (8.6)
(8.6) , то момент называется центральным
, то момент называется центральным (8.7)
(8.7) +…
+…  (8.8)
(8.8) (8.9
(8.9 (8.10)
(8.10) - центральный момент третьего порядка.
- центральный момент третьего порядка. = 0, то вариационный ряд является симметричным;
= 0, то вариационный ряд является симметричным; < 0, то вариационный ряд с левосторонней асимметрией;
< 0, то вариационный ряд с левосторонней асимметрией; (8.11)
(8.11)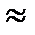 0, то распределение средневершинное;
0, то распределение средневершинное;
 - простая; (8.12)
- простая; (8.12) - взвешенная. (8.13)
- взвешенная. (8.13) . (8.14)
. (8.14)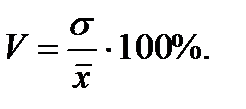 (8.15)
(8.15)
 . где М и m – число единиц генеральной и выборочной совокупности, обладающих определенным свойством; N и n – объемы генеральной и выборочной совокупности соответственно.
. где М и m – число единиц генеральной и выборочной совокупности, обладающих определенным свойством; N и n – объемы генеральной и выборочной совокупности соответственно. ; (12.1)
; (12.1)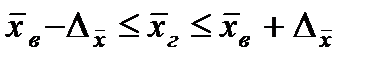 , (12.2)
, (12.2) и
и  - предельные ошибки выборки для доли и средней соответственно.
- предельные ошибки выборки для доли и средней соответственно.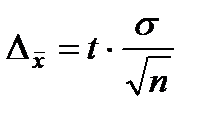



 . Если
. Если  , t=1,96; если
, t=1,96; если  , t=2,58.
, t=2,58. t находится по таблице t- распределения Стьюдента в соответствии с заданным уровнем доверительной вероятности
t находится по таблице t- распределения Стьюдента в соответствии с заданным уровнем доверительной вероятности  и числом степеней свободы k = n – 1. Оценка генеральной дисперсии служит «исправленная» выборочная дисперсия:
и числом степеней свободы k = n – 1. Оценка генеральной дисперсии служит «исправленная» выборочная дисперсия: . (12.3)
. (12.3)




 ; 1,05
; 1,05 


