
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое ожидание случайной величиныСодержание книги
Поиск на нашем сайте
Определение. Математическим ожиданием
где Для существования математического ожидания необходимо, чтобы ряд (6.1.1) сходился абсолютно, т.е.
в противном случае говорят, что математическое ожидание не существует. Пример 1. Пусть m Решение. Случайная величина
Применяя формулу (6.1.1), получим
Таким образом, математическое ожидание числа выпавших очков при бросании игрального кубика равно
Пример 2. Найти математическое ожидание случайной величины m Решение. Как известно, распределение случайной величины
где Используя формулу (6.1.1), получим
Таким образом, математическое ожидание числа успехов в схеме Бернулли равно
Определение. Математическим ожиданием
Условием существования математического ожидания непрерывной случайной величины является абсолютная сходимость интеграла
Пример 3. Найти математическое ожидание случайной величины
m Решение: Используя (6.1.3), получим
Пример 4. Найти математическое ожидание случайной величины
m Решение. Используя (6.1.3), получим
Делаем замену
Первое слагаемое равно нулю, т.к. равен нулю интеграл
Интеграл во втором слагаемом равен 1, т.к. этот интеграл равен функции распределения нормального закона с параметрами
Таким образом, математическое ожидание равно
Пример 5. Случайная величина
Проверить, имеет ли случайная величина m Решение. Проверим условие (6.1.4) существования математического ожидания
Математическое ожидание случайной величины
Математическое ожидание функции от случайной величины. Свойства математического ожидания
Пусть
В случае, если случайная величина
При этом условие существования математического ожидания (6.1.4) примет вид:
Пример 6. Случайная величина
Найти математическое ожидание математической величины: m Решение. Для решения задачи применим формулу (6.2.1).
Таким образом, математическое ожидание математической величины
Пусть
Условие существования математического ожидания случайной величины
Пример 7. Случайная величина
Найти математическое ожидание случайной величины m Решение. Используя формулу (6.2.4), получаем:
Пример 8. Случайная величина
Найти математическое ожидание случайной величины m Решение. Используя формулу (6.2.4.), получаем:
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 138; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.52.29 (0.007 с.) |

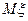 дискретной случайной величины
дискретной случайной величины 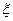 называется выражение, вычисляемое по формуле:
называется выражение, вычисляемое по формуле: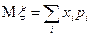 , (6.1.1)
, (6.1.1)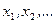 — значения случайной величины,
— значения случайной величины,  — соответствующие им вероятности, которые определяются равенством
— соответствующие им вероятности, которые определяются равенством 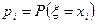 .
.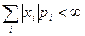 , (6.1.2)
, (6.1.2)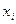
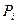

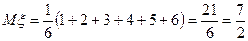 .
.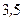 . l
. l
 — вероятность «успеха»,
— вероятность «успеха»,  ,
, 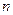 — количество испытаний в схеме Бернулли.
— количество испытаний в схеме Бернулли.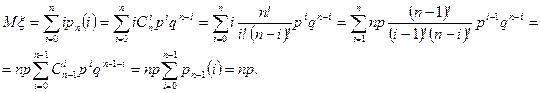
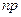 . l
. l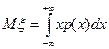 . (6.1.3)
. (6.1.3)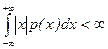 . (6.1.4)
. (6.1.4)
 . l
. l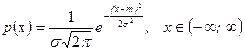 .
. . (6.1.5)
. (6.1.5)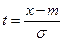 или
или 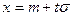 . В этом случае (6.1.5) примет вид:
. В этом случае (6.1.5) примет вид: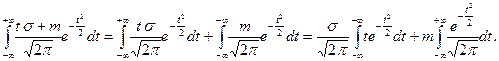 (6.1.6)
(6.1.6)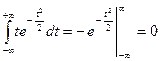 .
.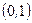 при значении аргумента равным
при значении аргумента равным 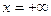 , т.е.
, т.е. .
.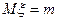 . l
. l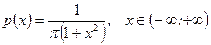 . (6.1.7)
. (6.1.7) .
. — функция от случайной величины. Определим математическое ожидание
— функция от случайной величины. Определим математическое ожидание 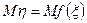 . Это возможно сделать двумя способами. Первый способ состоит в том, что сначала строится распределение случайной величины
. Это возможно сделать двумя способами. Первый способ состоит в том, что сначала строится распределение случайной величины 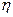 , затем уже находим
, затем уже находим 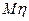 . Мы рассмотрим другой способ. Пусть сначала
. Мы рассмотрим другой способ. Пусть сначала 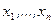 . Тогда случайная величина
. Тогда случайная величина  с теми же вероятностями
с теми же вероятностями 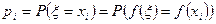 . В этом случае математическое ожидание определяется по формуле
. В этом случае математическое ожидание определяется по формуле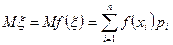 . (6.2.1)
. (6.2.1)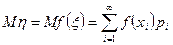 . (6.2.2)
. (6.2.2)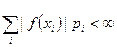 . (6.2.3)
. (6.2.3)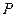
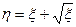 .
.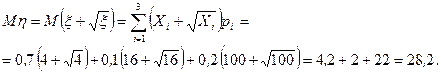
 . Пусть функция
. Пусть функция  непрерывная (за исключением, быть может, счетного числа точек). Тогда математическое ожидание случайной величины
непрерывная (за исключением, быть может, счетного числа точек). Тогда математическое ожидание случайной величины 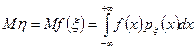 . (6.2.4)
. (6.2.4) . (6.2.5)
. (6.2.5)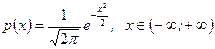 .
.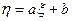 .
.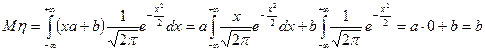 . l
. l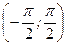 , т.е.
, т.е.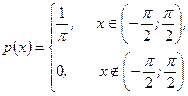
 .
.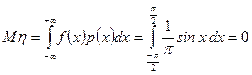 . l
. l


