
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод максимального правдоподобияСодержание книги
Поиск на нашем сайте
Метод максимального правдоподобия является наиболее распространенным методом нахождения оценок. Метод максимального правдоподобия опирается на использование условий экстремума функций одной или нескольких случайных величин. В качестве такой функции используется функция правдоподобия. Определение. Функцией правдоподобия называется функция
в дискретном случае и
в непрерывном случае. В функции правдоподобия Определение. Оценкой максимального правдоподобия называется такое
Поскольку Определение. Уравнением правдоподобия называется уравнение
В случае, когда теоретическая функция распределения
Пример 4. Найти оценки параметров m Решение. Нормальный закон распределения характеризуется плотностью распределения
Функция правдоподобия примет вид:
Логарифмируя выражение (8.3.6), получим
Подставляя (8.3.7) в систему (8.3.5), получим
Из первого уравнения системы (8.3.8) получаем
а из второго уравнения системы (8.3.8), с учетом (8.3.9), получаем
Следует отметить, что полученная оценка является смещенной. Читателю предлагается самостоятельно показать, что
Интервальные оценки (доверительные интервалы)
Статистическая оценка § к каким ошибкам может привести замена параметра § с какой степенью надежности можно ожидать, что получаемые ошибки не выйдут за известные пределы.
Определение. Интервальной оценкой (доверительным интервалом) называется числовой интервал
где Доверительная вероятность и уровень значимости связаны соотношением
По заданной оценке § двусторонние; § односторонние. Ограничимся нахождением двусторонних доверительных интервалов. Односторонние доверительные интервалы находятся аналогично. Для каждой доверительной вероятности
Определение. Величину Определение. Квантилем уровня
Теорема. Пусть плотность случайной величины Доказательство.
т.к. ввиду симметричности закона распределения относительно оси
Рассмотрим теперь правила построения доверительных интервалов для некоторых параметров распределения.
|
|||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 159; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.91.15 (0.01 с.) |

 (8.3.1)
(8.3.1) (8.3.2)
(8.3.2) элементы выборки
элементы выборки 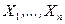 являются фиксированными параметрами, а
являются фиксированными параметрами, а  — аргументом.
— аргументом. , для которого
, для которого . (8.3.3)
. (8.3.3) и
и  принимают максимум при одном и том же значении аргумента
принимают максимум при одном и том же значении аргумента  . (8.3.4)
. (8.3.4)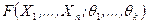 зависит от нескольких параметров
зависит от нескольких параметров  , при применении метода максимального правдоподобия вместо уравнения (8.3.4) необходимо использовать систему уравнений
, при применении метода максимального правдоподобия вместо уравнения (8.3.4) необходимо использовать систему уравнений (8.3.5)
(8.3.5) (математическое ожидание) и
(математическое ожидание) и  (дисперсия) нормального закона распределения.
(дисперсия) нормального закона распределения. .
.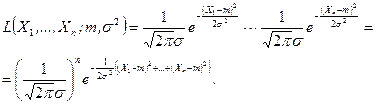 (8.3.6)
(8.3.6) . (8.3.7)
. (8.3.7) (8.3.8)
(8.3.8) , (8.3.9)
, (8.3.9)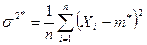 .
. и
и 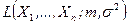 . l
. l , будучи функцией случайной выборки (статистикой), сама является случайной величиной, имеющей свой закон распределения и числовые характеристики (параметры) распределения. При малом числе наблюдений могут возникнуть следующие задачи:
, будучи функцией случайной выборки (статистикой), сама является случайной величиной, имеющей свой закон распределения и числовые характеристики (параметры) распределения. При малом числе наблюдений могут возникнуть следующие задачи: , определяемый по результатам выборки, относительно которого можно утверждать с определенной, близкой к единице, вероятности, что он заключает в себе значение оцениваемого параметра генеральной совокупности, т.е.
, определяемый по результатам выборки, относительно которого можно утверждать с определенной, близкой к единице, вероятности, что он заключает в себе значение оцениваемого параметра генеральной совокупности, т.е. , (8.4.1)
, (8.4.1) и
и  — нижняя и верхняя (левая и правая) границы доверительного интервала параметра
— нижняя и верхняя (левая и правая) границы доверительного интервала параметра  — доверительная вероятность.
— доверительная вероятность. .(8.4.2)
.(8.4.2) , что
, что . (8.4.3)
. (8.4.3) , при котором значение соответствующей функции распределения равно
, при котором значение соответствующей функции распределения равно  . (8.4.4)
. (8.4.4) , и пусть
, и пусть 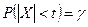 . Тогда
. Тогда  — квантиль уровня
— квантиль уровня  распределения случайной величины
распределения случайной величины  ,
,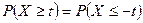 . Отсюда следует, что
. Отсюда следует, что и
и  . n
. n


