
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительный интервал для дисперсии генеральной совокупности, имеющей нормальное распределение при известном математическом ожидании.Содержание книги
Поиск на нашем сайте
Предположим, что выборка
В этом случае статистика Доверительный интервал для дисперсии при известном математическом ожидании имеет вид:
где Таким образом, доверительный интервал для дисперсии при известном математическом ожидании строится следующим образом: 1. Используя выборку 2. Вычисляем квантили 3. По формуле (8.4.12) получаем искомый доверительный интервал.
Замечание. Квантили § используя таблицы § используя функцию ХИ2ОБР (вероятность;степени_свободы) из EXCEL, при этом аргумент «вероятность» данной функции должен быть равен уровню значимости, а аргумент «степени_свободы» должен быть равен § используя функцию qchisq(p, d) из MATHCAD, при этом переменные данной функции должны быть равны:
Аналогично строится доверительный интервал для дисперсии генеральной совокупности, имеющей нормальное распределение при неизвестном математическом ожидании. В качестве оценки неизвестной дисперсии
В этом случае статистика Доверительный интервал для дисперсии при неизвестном математическом ожидании имеет вид:
где Таким образом, доверительный интервал для дисперсии при неизвестном математическом ожидании строится следующим образом: 1. Вычисляем оценку 2. Вычисляем квантили 3. По формуле (8.4.14) получаем искомый доверительный интервал.
Пример 5. Найти доверительный интервал с доверительной вероятностью 0,95 для оценки математического ожидания, нормально распределенной случайной величины
m Решение. По условию задачи Применив (8.4.6), получим
Пример 6. Случайная величина
Требуется: 1) построить доверительный интервал для оценки математического ожидания, если доверительная вероятность равна 0,97; 2) построить доверительный интервал для оценки дисперсии, если доверительная вероятность равна 0,95. m Решение. Для оценки математического ожидания будем использовать формулу (8.4.9), т.к. дисперсия неизвестна. Вычислим все величины, присутствующие в (8.4.9). Объем выборки Оценка математического ожидания:
Исправленная выборочная дисперсия:
Корень квадратный исправленной выборочной дисперсии:
Для доверительной вероятности Доверительный интервал имеет вид:
и окончательно
Перейдем ко второй части задачи. Для оценки дисперсии будем использовать формулу (8.4.14), т.к. математическое ожидание неизвестно. Для данной формулы необходимо вычислить квантили Доверительный интервал имеет вид:
и окончательно
Глава 9. Проверка статистических гипотез
Основные понятия
Определение. Статистической гипотезой называется любое предположение Определение. Правило, по которому гипотеза Проверяемую гипотезу Схема проверки нулевой гипотезы: 1. Используя проверочные данные
2. По случайной выборке 3. По заранее выбранной малой вероятности
Таблица 9.1
Определение. Вероятность Определение. Вероятность Если использовать терминологию качества продукции, то Возможны три варианта расположения критической области: 1. Правосторонняя критическая область (рис 9.1), состоящая из интервала 2. Левосторонняя критическая область (рис 9.2), состоящая из интервала 3. Двусторонняя критическая область (рис 9.3), состоящая из интервалов
В следующих параграфах рассмотрим несколько конкретных практических примеров.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.165.235 (0.01 с.) |

 произведена из нормальной генеральной совокупности с неизвестной дисперсией при известном математическом ожидании, равном
произведена из нормальной генеральной совокупности с неизвестной дисперсией при известном математическом ожидании, равном  . В качестве оценки неизвестной дисперсии
. В качестве оценки неизвестной дисперсии  возьмем выборочную дисперсию
возьмем выборочную дисперсию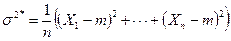 . (8.4.11)
. (8.4.11) будет иметь
будет иметь  –распределение с
–распределение с 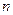 степенями свободы.
степенями свободы. , (8.4.12)
, (8.4.12) — квантиль уровня
— квантиль уровня 
 и
и 

 .
. . (8.4.13)
. (8.4.13)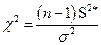 будет иметь
будет иметь  степенью свободы.
степенью свободы. , (8.4.14)
, (8.4.14) — квантиль уровня
— квантиль уровня  , которая является средним арифметическим элементов выборки
, которая является средним арифметическим элементов выборки  , если известны ее дисперсия
, если известны ее дисперсия  , выборочная средняя
, выборочная средняя  и объем выборки
и объем выборки  .
. . Найдем квантиль
. Найдем квантиль 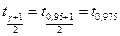 нормального распределения с параметрами
нормального распределения с параметрами 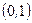 , используя, например EXCEL: применяя функцию НОРМСТОБР(0,975), получим
, используя, например EXCEL: применяя функцию НОРМСТОБР(0,975), получим  .
.
 l
l

 .
. .
. .
.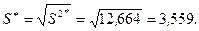
 найдем квантиль
найдем квантиль 
 ‑распределения) с
‑распределения) с  числом степеней свободы. Для этого используем, например, функцию qt(p, d) из MATHCAD:
числом степеней свободы. Для этого используем, например, функцию qt(p, d) из MATHCAD:  .
.
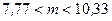 .
. и
и  . Используя функцию qchisq(p, d) из MATHCAD, получим:
. Используя функцию qchisq(p, d) из MATHCAD, получим:  и
и  .
.
 . l
. l (гипотеза) о виде закона распределения генеральной совокупности или о числовых значениях параметров закона распределения.
(гипотеза) о виде закона распределения генеральной совокупности или о числовых значениях параметров закона распределения. называют альтернативной.
называют альтернативной. и учитывая условия задачи, принимают нулевую гипотезу
и учитывая условия задачи, принимают нулевую гипотезу  , называемая статистикой, для которой будет известен точный или приближённый закон распределения.
, называемая статистикой, для которой будет известен точный или приближённый закон распределения. определяется критическая область
определяется критическая область  , для которой
, для которой 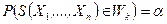 . И если величина
. И если величина  , вычисляется при конкретной выборке
, вычисляется при конкретной выборке  , то гипотеза
, то гипотеза 


 не допустить ошибку второго рода называется мощностью критерия.
не допустить ошибку второго рода называется мощностью критерия. , где
, где  определяется из условия:
определяется из условия:  . (9.1.1)
. (9.1.1) , где
, где 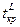 определяется из условия:
определяется из условия:  . (9.1.2)
. (9.1.2)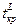 и
и  и
и  . (9.1.3)
. (9.1.3)



