
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 1. Случайные события и их вероятностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Введение
Цель данного пособия помочь студенту самостоятельно подготовиться к выполнению контрольных работ. При написании пособия авторы не ставили своей целью дать систематическое изложение теоретического материала. Перед каждой рассматриваемой задачей дается тот теоретический материал, который необходим для ее решения. Если студент ранее овладел необходимым теоретическим материалом, то вводную часть каждой задачи он может опустить и перейти непосредственно к решению задачи. Необходимо отметить, что приведенный теоретический материал достаточно полно охватывает курс указанного предмета. Авторы надеются, что пособие будет полезно студентам в овладении методами решения основных задач курса теории вероятностей и математической статистики. Глава 1. Случайные события и их вероятности
Общее определение и свойства вероятности
Определение. Вероятностью § Для каждого события
§ Для достоверного события
§ Если
Свойства вероятности: 1. Вероятность события
Доказательство. Используем очевидное свойство суммы противоположных событий
Из двух последнего равенства следует, что
2. Вероятность невозможного события равна нулю, т.е.
Доказательство. Используем очевидное свойство
откуда и следует данное свойство. n
3. Если событие
Доказательство. Представим событие Используя теорему сложения для несовместных событий, получим:
4. Для каждого события
Доказательство. Данное свойство следует из условий нормировки и теоремы сложения для несовместных событий. n
ГЛАВА 2. Классическая и геометрическая вероятности Классическое определение вероятности
Вернемся к монете. Пространство элементных исходов
В силу того, что монета симметрична, нельзя предпочесть «герб» «решке» (или наоборот). Следовательно, обоим элементарным исходам необходимо сопоставить одинаковую вероятность
Откуда получаем:
Рассмотрим общий случай. Пусть пространство Далее рассмотрим некоторое событие
Таким образом, в классической схеме вероятность любого события Пример 1. В урне находятся m Решение. Число всевозможных исходов равно
Число благоприятных исходов равно
Таким образом, используя классическое определение вероятности, получаем
Пример 2. Имеются две урны: в первой – m Решение. Каждый шар из первой урны может комбинировать с каждым шаром из второй урны. Следовательно, число всевозможных исходов:
Аналогично, число благоприятных исходов:
Следовательно, используя классическое определение вероятности, получаем:
Пример 3. Из колоды карт (36 листов) наудачу выбирается одна карта. Определить вероятность того, что она окажется тузом (событие А). m Решение. Число всевозможных исходов равно:
Число благоприятных исходов равно числу тузов, т.е.
Таким образом, используя классическое определение вероятности, получаем:
Условная вероятность
Рассмотрим следующий пример. Бросаются две игральные кости. Найдем вероятность того, что сумма выпавших очков равна 8, если заранее известно, что сумма выпавших очков есть четное число. Всевозможные исходы запишем в виде таблицы 3.1: Таблица 3.1
Из таблицы видно, что число всевозможных исходов равно 36, но число исходов, удовлетворяющих условию, при которых сумма очков есть четное число, равно 18. Из них ровно в 5 исходах сумма очков равна 8. Пользуясь классическим определением вероятности, находим, что искомая вероятность равна Заметим, что безусловная вероятность того, что сумма выпавших очков, равная 8, равна Найдем условную вероятность
Разделив числитель и знаменатель на число всевозможных исходов
Последняя формула может служить общим определением условной вероятности при аксиоматическом подходе. Определение. Условной вероятностью
Пример 1. При трехкратном подбрасывании монеты выпало два «герба». Найти условную вероятность того, что при втором подбрасывании выпал «герб». m Решение. Рассмотрим следующие события:
Событию Число всевозможных исходов при трехкратном подбрасывании монеты
Аналогично, событию
Далее, применяя (3.1.1), получаем искомую вероятность
Независимость событий
Определение. События A и B называются независимыми, если условная вероятность события A при условии B совпадает с безусловной вероятностью события A, т.е.
Можно сформулировать и другое определение независимых событий Определение. События A и B независимы, если
Очевидно, что данные два определения равносильны. Пример 7. Пусть события m Решение. Применяя определение независимости событий, и используя вероятность противоположного события, имеем
Пример 8. Зависимы или независимы несовместные события. m Решение. Пусть события Таким образом, несовместные события зависимы. l
Пример 9. Из полной колоды карт (52 листа) вынимается одна карта. Рассматриваются следующие события:
Зависимы или независимы следующие пары событий: 1) M Решение.
Определение. События
Замечание. Из попарной независимости событий
Пример 10. Пусть эксперимент состоит в выборе одного из четырех шаров. Пусть три из них занумерованы цифрами 1, 2, 3, а на четвертом шаре имеются все эти цифры. Обозначим через m Решение. Так как, каждая цифра встречается дважды, то
Так как две различные цифры присутствуют только на одном шаре, то
следовательно, события Все три различные цифры присутствуют только на одном шаре
Таким образом, получаем, что события
Формула полной вероятности Определение. События § они попарно несовместны, т.е. § в результате опыта одно из событий обязательно должно произойти, т.е. Пусть имеется некоторое событие
Событие
причем события Тогда по аксиоме сложения:
Далее, применяя теорему умножения вероятностей
Это и есть формула полной вероятности.
Пример 11. Имеются две урны: в первой m Решение. Пусть искомое событие
Очевидно, что
Теперь по формуле полной вероятности (3.4.1) получаем:
Пример 12. В условиях предыдущей задачи из первой урны перекладывают сразу три шара (предполагается, что m Решение. Пусть искомое событие
Так как во второй урне 3 шара принадлежат 1-ой урне, а
Вероятность появления белого шара из первой урны не зависит от того, вынимается ли этот шар непосредственно из первой урны или после перекладывания во вторую. Следовательно, условная вероятность появления белого шара при условии того, что он изначально находился в первой урне, равна:
Аналогично условная вероятность появления белого шара при условии того, что он изначально находился во второй урне, равна:
По формуле полной вероятности (3.4.1) получаем:
Пример 13. Среди 30 экзаменационных билетов: 25 «хороших» и 5 «плохих». Какова вероятность, отвечая вторым, взять «хороший» билет? m Решение. Пусть искомое событие
Очевидно, что
По формуле полной вероятности (3.4.1), получим:
Формула Байеса
Пусть имеется полная группа несовместных событий По определению условной вероятности (3.4.1), имеем:
Далее, применяя теорему умножения вероятностей
Последняя формула называется формулой Байеса или формулой гипотез (события Если после опыта, который заканчивается появлением события
Пример 14. Имеются три урны: в первой — m Решение. Пусть искомое событие
Очевидно, что:
Условные вероятности равны:
По формуле полной вероятности (3.4.1), находим, что
По формуле Байеса (3.5.1), находим:
Аналогично получаем, что
Пример 15. Имеются две урны: в первой — m Решение. Рассмотрим следующие гипотезы:
Очевидно, что вероятности выбора урн равны:
Находим условные вероятности:
По формуле полной вероятности (3.4.1), получаем:
По формуле Байеса (3.5.1), получаем:
Далее применяем (3.5.2):
Условная вероятность появления второго белого шара при условии, что была выбрана первая урна, и из нее вынут белый шар:
Аналогично:
В итоге:
Формула Бернулли Определение. Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два исхода, и вероятности исходов остаются неизменными для всех испытаний. Обычно эти две вероятности обозначаются через
Пространство элементарных исходов каждого отдельного испытания состоит из двух исходов 1 и 0. Очевидно, пространство элементарных исходов
Но на практике нас, как правило, интересует не порядок появления успехов в последовательности Теорема. Вероятность
где Доказательство. Событие «в
Число успехов в
Пример 1. Стрелок попадает в мишень с вероятностью a) ровно четыре раза; б) не менее трех раз. m Решение. Для решения данной задачи применим формулу (4.1.2), в которой:
а) Число успехов равно
б) Обозначим
Пример 2. Сколько испытаний с вероятностью успеха m Решение. Рассмотрим следующие события:
Для решения задачи используем формулу (4.1.2), согласно которой вероятность того, что успехов не будет (т.е. число успехов равно нулю), равна:
Используя свойство вероятности противоположного события, получаем, что вероятность того, что будет хотя бы один успех, равна:
Остается найти наименьшее целое
Решим последнее неравенство.
Разделив последнее неравенство на
Наименьшим целым числом
Пример 3. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен): а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми. m Решение. Так как противники равносильны и ничейный исход партии исключен, то вероятности выигрыша и проигрыша каждой партии одинаковы и а) Вероятность выигрыша трех партий из четырех равна:
а вероятность выигрыша пяти партий из восьми равна:
Так как б) Вероятность выигрыша не менее трех партий из четырех равна:
а вероятность выигрыша не менее пяти партий из восьми равна:
Так как
Формула Пуассона
При больших значениях числа испытаний
и не мало, и не велико. В таких случаях удобно использовать для вероятности
При
Следовательно, (4.2.2) примет вид:
а это и есть формула Пуассона. Замечание. При выводе формулы Пуассона (4.2.3) использовалось то, что Замечание. Формула Пуассона (4.2.3) зависит от § можно воспользоваться Приложением 1; § используя функцию ПУАССОН (x;среднее;интегральная) из EXCEL; в которой аргумент x равен числу «успехов» § используя функцию dpois(k, l) из MATHCAD, в которой
Пример 4. Найти вероятность того, что среди 1460 человек ровно трое родились 29 февраля. m Решение. Вероятность того, что один конкретный человек родился 29 февраля, равна Далее находим коэффициент
Применяя (4.2.2), получаем:
Пример 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность того, что при 5000 выстрелах в цель попало не менее двух выстрелов. m Решение. Рассмотрим два противоположных события:
Найдем вероятность события | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 события
события  называется функция, определенная на пространстве элементарных исходов и удовлетворяющая трем условиям:
называется функция, определенная на пространстве элементарных исходов и удовлетворяющая трем условиям: (условие неотрицательности);
(условие неотрицательности);
 (условие нормировки);
(условие нормировки); , то
, то (теорема сложения для несовместных событий).
(теорема сложения для несовместных событий). , противоположного событию
, противоположного событию  .
.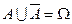 . Тогда, используя условие нормировки и теорему сложения для несовместных событий, получим:
. Тогда, используя условие нормировки и теорему сложения для несовместных событий, получим: ,
, . n
. n .
. и теорему сложения для несовместных событий, получим:
и теорему сложения для несовместных событий, получим: ,
,
 , то
, то .
. ,
,  .
. . n
. n .
. — появление «герба»;
— появление «герба»; — появление «решки».
— появление «решки». . Далее очевидно, что
. Далее очевидно, что .
. .
.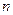 всевозможных равнозначных исходов
всевозможных равнозначных исходов  . Теперь каждому элементарному исходу
. Теперь каждому элементарному исходу  поставим в соответствие вероятность
поставим в соответствие вероятность  .
. (благоприятных) элементарных исходов
(благоприятных) элементарных исходов  .
. Положим
Положим . (2.1.1)
. (2.1.1)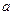 белых и
белых и  черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар белый (событие
черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар белый (событие  .
. .
. . l
. l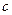 белых и
белых и  черных шаров. Из каждой урны вынимается по шару. Найти вероятность того, что оба шара будут белыми (событие А).
черных шаров. Из каждой урны вынимается по шару. Найти вероятность того, что оба шара будут белыми (событие А). .
. .
. . l
. l .
. .
. . l
. l .
. , т.е. задание дополнительного условия может повлиять на вычисление вероятности.
, т.е. задание дополнительного условия может повлиять на вычисление вероятности. события
события  уже произошло. Для простоты рассмотрим классическую схему. Естественно положить, что данная вероятность есть отношение числа исходов
уже произошло. Для простоты рассмотрим классическую схему. Естественно положить, что данная вероятность есть отношение числа исходов  , благоприятных совместному (одновременному) осуществлению событий
, благоприятных совместному (одновременному) осуществлению событий  .
.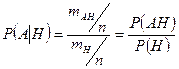 .
. . (3.1.1)
. (3.1.1) соответствует два исхода: Г – Г – Р, Р – Г – Г.
соответствует два исхода: Г – Г – Р, Р – Г – Г. . Отсюда находим:
. Отсюда находим: .
. .
. . l
. l . (3.3.1)
. (3.3.1) . (3.3.2)
. (3.3.2)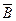 ,
,  , т.е.
, т.е.  ;
;
 , т.е.
, т.е.  . l
. l , причем
, причем  . Тогда
. Тогда  , т.к. события не пересекаются. Следовательно
, т.к. события не пересекаются. Следовательно  — появление бубнового туза.
— появление бубнового туза. ,
,  , следовательно, события независимы;
, следовательно, события независимы; ,
,  , следовательно, события зависимы;
, следовательно, события зависимы; , следовательно, события зависимы. l
, следовательно, события зависимы. l независимы в совокупности, если для всех
независимы в совокупности, если для всех
 , выполнено равенство
, выполнено равенство
 и
и 
 не следует, что события
не следует, что события  событие, состоящее в том, что на выбранном шаре имеется цифра
событие, состоящее в том, что на выбранном шаре имеется цифра 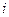 . Зависимы ли события
. Зависимы ли события  ,
,  и
и  .
. .
. ,
, и
и  .
. образуют полную группу несовместных событий (являются гипотезами), если они удовлетворяют двум требованиям:
образуют полную группу несовместных событий (являются гипотезами), если они удовлетворяют двум требованиям: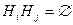 при
при  ;
; .
. и условные вероятности
и условные вероятности  . Найдем вероятность
. Найдем вероятность 
 ,
, при
при  и
и  несовместны.
несовместны. .
. , получаем:
, получаем: . (3.4.1)
. (3.4.1) — переложен белый шар;
— переложен белый шар; — переложен черный шар.
— переложен черный шар.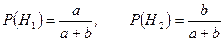 ;
; .
. . l
. l и
и  ). Найти вероятность того, что шар, взятый из второй урны, будет белым.
). Найти вероятность того, что шар, взятый из второй урны, будет белым. принадлежат 2-ой, то вероятности гипотез равны:
принадлежат 2-ой, то вероятности гипотез равны: .
. .
. .
. . l
. l ;
; .
. . l
. l , если известно, что событие
, если известно, что событие 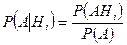 .
. , получаем
, получаем . (3.5.1)
. (3.5.1) , а новые
, а новые  :
: . (3.5.2)
. (3.5.2) белых шаров. Выбирается наугад урна и из нее вынимается шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.
белых шаров. Выбирается наугад урна и из нее вынимается шар. Этот шар оказался белым. Найти вероятность того, что этот шар вынут из первой, второй или третьей урны.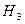 — выбрана третья урна.
— выбрана третья урна. .
. .
. .
. .
. ,
, 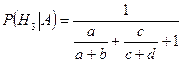 . l
. l .
.
 .
.
 .
. .
. .
. .
. . l
. l и
и  , исход с вероятностью
, исход с вероятностью  . (4.1.1)
. (4.1.1) последовательностей из
последовательностей из  равна:
равна: .
.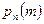 того, что в
того, что в  , (4.1.2)
, (4.1.2) » содержит столько элементарных исходов, сколько существует способов размещения
» содержит столько элементарных исходов, сколько существует способов размещения  . А так как вероятность конкретной последовательности, содержащей
. А так как вероятность конкретной последовательности, содержащей  , то в итоге получаем:
, то в итоге получаем: , тогда
, тогда  . Очевидно, что
. Очевидно, что  . Отсюда следует, что
. Отсюда следует, что .
. . Найти вероятность того, что в результате пяти независимых выстрелов стрелок попадает:
. Найти вероятность того, что в результате пяти независимых выстрелов стрелок попадает: .
. .
. — вероятность попадания не менее трех раз из пяти.
— вероятность попадания не менее трех раз из пяти.
 . l
. l нужно произвести, чтобы вероятность хотя бы одного успеха была не меньше 0,5?
нужно произвести, чтобы вероятность хотя бы одного успеха была не меньше 0,5? .
. .
. .
.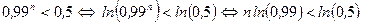 .
. , получим
, получим .
. . l
. l .
. ,
, .
.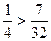 , то вероятнее выиграть три партии из четырех.
, то вероятнее выиграть три партии из четырех.

 , то вероятнее выиграть не менее пяти партий из восьми. l
, то вероятнее выиграть не менее пяти партий из восьми. l . Пусть число испытаний
. Пусть число испытаний  (4.2.1)
(4.2.1)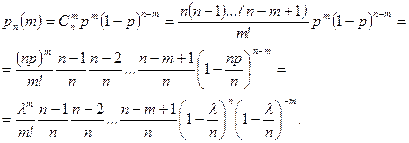 (4.2.2)
(4.2.2) и сделанных выше допущениях очевидны следующие приближения:
и сделанных выше допущениях очевидны следующие приближения: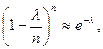
 ,
,  .
. , (4.2.3)
, (4.2.3) . Значения функции (4.2.2) можно определить следующими способами:
. Значения функции (4.2.2) можно определить следующими способами: и
и  .
. , т.к. 29 февраля бывает ровно 1 раз в 4 года.
, т.к. 29 февраля бывает ровно 1 раз в 4 года. .
. . l
. l


