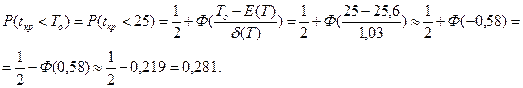Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Управление проектом с неопределенным (вероятностным) временем выполнения работСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В методе критического пути предполагалось, что время выполнения работ нам известно. На практике, и это характерно для инновационного проекта, сроки заданы вероятностными величинами. Можно строить некоторые предположения о времени выполнения каждой работы, но нельзя предусмотреть все возможные трудности или задержки выполнения. Для управления проектом с вероятностным временем выполнения работ наиболее широкое применение получил метод анализа и оценки программ (проектов) – метод PERT, рассчитанный на использование вероятностных оценок времени выполнения работ, предусматриваемых проектом. Для каждой работы вводят три оценки: * оптимистическое время a – наименьшее возможное время выполнения работы; * пессимистическое время b – наибольшее возможное время выполнения работы; * наиболее вероятное время m – ожидаемое время выполнения работы в нормальных условиях. По a, b и m находят ожидаемое время выполнения работы:
и дисперсию ожидаемой продолжительности t:
Используя значения t, найдем критический путь сетевого графика. Распределение времени T завершения проекта является нормальным со средним E(T), равным 2 сумме ожидаемых значений времени работ на критическом пути, и дисперсией d (T), равной сумме дисперсий работ критического пути, если времена выполнения каждой из работ можно считать независимыми друг от друга. Тогда мы можем рассчитывать вероятность завершения проекта в установленный срок To:
где
16. Применение диаграммы Ганта при планировании инновационного проекта; Простейший метод планирования можно отобразить, используя метод диаграмм (графика) Ганта, предложенный инженером Генри Гантом в 1917г. Диаграмма или график Ганта представляет собой линейный график, задающий сроки начала и окончания взаимосвязанных действий, образующий единый технологический процесс, который необходимо выполнить для достижения цели проекта (рис 11).
Работа 1
Работа 2
Работа 3
Работа 4
Работа 5
Рис.11. Диаграмма Ганта График Ганта, при использовании промежуточных результатов достижения инновационного проекта в общем виде может выглядеть следующим образом (рис.12).
Рис. 12. Диаграмма Ганта по инновационному проекту
Этот метод, впрочем как и остальные, имеет достоинства и недостатки. К основному достоинству необходимо отнести простоту и наглядность, к недостаткам – сложность формализации процедур анализа отображенных диаграмм и сложность в установлении зависимостей между различными действиями в графике. В современных системах планирования проектов используют модифицированные диаграммы Ганта, в которых основные недостатки устранены. 17. Планирование инновационного проекта на основе сетевого графика: основные понятия и определения; Планирование, по сути, – создание плана, который может иметь различную форму, например форму диаграммы, таблицы с цифрами, графика или последовательности действий. Для того чтобы говорить о планировании инновационного проекта на основе сетевого графика, необходимо определиться с основными понятиями и определениями. Сетевой график – это графическое представление логической последовательности работ в целях выполнения проекта. Представление работ в виде логической последовательности означает, что они отображаются исключительно в той последовательности, в которой они должны следовать, если не принимать во внимание временные факторы. Логическая последовательность работ бывает следующей. Работы могут выполняться последовательно и параллельно. Последовательно работы выполняются в том случае, если для начала следующей работы необходимо иметь результат предыдущей. В то же время другие работы могут выполняться параллельно к работам, выполняющимся последовательно. Такая возможность распараллелить работы над проектом и образует базу для построения сетевого графика. Введем основные понятия теории сетевого планирования и управления. Таких основных понятий можно выделить два: работа и событие. Работа – это любое действие или совокупность действий, которые необходимо выполнить для реализации проекта и которые могут быть рассмотрены в целях удобства как неразложимые на более элементарные действия. Для работы главными характеристиками являются время и ресурсы, необходимые для ее выполнения. Время выполнения работы определяется экспертно или расчетным путем на основе коэффициентов трудоемкости. Под ресурсами понимаются любые материальные, энергетические или информационные компоненты, необходимые для ее выполнения. Событием называется результат работы. Событие представляет собой одномоментную характеристику, которая не имеет ресурсных параметров. На сетевом графике события изображаются в виде геометрических фигур, чаще всего в виде кружков или квадратиков, в которых проставляются номера событий. Изображение работ в сетевом графике зависит от того, какой тип графика применяется для управления проектом. Существуют 3 вида сетевого графика в зависимости от способа изображения работ и событий: 1) в терминах работ и событий; 2) в терминах работ; 3) в терминах событий. Сетевой график в терминах работ и событий представляет из себя такой сетевой график, в котором события изображаются в виде геометрических фигур, а работы в виде стрелок, выходящих из одного события, которое мы будем называть предыдущим, и входящих во второе, которое мы будем называть последующим событием для рассматриваемой работы.
Сетевым графиком в терминах работ называется график, в котором представлена только последовательность работ. Работы в этом типе сетевого графика изображаются в виде геометрических фигур и соединяются между собой стрелками, которые изображают логическую последовательность работ в проекте. В геометрические фигуры вписываются параметры работы: ее название, время выполнения, ресурсы и прочая необходимая для выполнения работы информация. Наиболее редким типом сетевого графика является сетевой график в терминах событий. В этом сетевом графике события представлены в виде геометрических фигур, соединенных между собой стрелками. Эти стрелки показывают только логический порядок следования событий и их нельзя путать с работами в сетевом графике в терминах работ и событий. Рассмотрим теперь основные понятия теории сетевых графиков, которые будут использоваться при дальнейшем изложении. Весом работы мы будем называть любой числовой параметр, связанный с этой работой. Так, весами для работы может выступать время выполнения работы, ресурсы. Путем Lij из события i в событие j в сетевом графике называется множество работ, соединяющих эти два события друг с другом. Длиной пути Lij называют сумму весов работ, входящих в данный путь.
где { Lij } – множество работ, лежащих на пути Lij, tij – вес работы (i, j). Начальным событием в сетевом графике называется событие, в котором нет входящих работ.
Конечным событием сетевого графика называется событие, в котором нет исходящих работ.
Фиктивной работой называется работа, которая не имеет длительности. Такая работа применяется для осуществления логической связки между событиями в том случае, если работа не может начаться без окончания некоторого события, причем между этим событием и событием, из которого начинается работа, не существует никакой реальной работы.
События на сетевом графике обозначаются числами. Нумерация событий может осуществляться в любом порядке, но нужно соблюдать следующее правило: номер предыдущего события должен быть меньше, чем последующего. В этом случае нумерация называется правильной. Такое требование к нумерации событий в сетевом графике обусловлено существованием алгоритмов расчета ряда параметров. При произвольном порядке нумерации событий будет невозможен правильный обход всех ветвей сетевого графика. Работы в этом случае обозначаются двумя цифрами, заключенными в круглые скобки и разделенные точкой с запятой. Первая цифра означает номер предыдущего события, а вторая - номер последующего. Например:
Планирование инновационного проекта на основе сетевого графика: виды сетевых графиков 19. Планирование инновационного проекта на основе сетевого графика: правила построения сетевого графика; Сетевой график – это графическое представление логической последовательности работ в целях выполнения проекта. Представление работ в виде логической последовательности означает, что они отображаются исключительно в той последовательности, в которой они должны следовать, если не принимать во внимание временные факторы. Логическая последовательность работ бывает следующей. Работы могут выполняться последовательно и параллельно. Последовательно работы выполняются в том случае, если для начала следующей работы необходимо иметь результат предыдущей. Рассмотрим теперь некоторые правила, которыми нужно руководствоваться при построении сетевого графика. Правило 1. В сетевом графике должно быть только одно начальное и только одно конечное событие. Это правило тоже связано с наличием алгоритмов расчета сетевых графиков. В том случае, если такое правило не выполняется, это может привести к неоднозначности алгоритма. Если проект, лежащий в основе сетевого графика, предполагает наличие нескольких начальных событий (например, несколько предпосылок для проведения проектов) или наличие нескольких конечных событий (например, несколько целей своего осуществления), то в этом случае необходимо ввести фиктивное начальное (или конечное) событие, и соединить его с начальными (конечными) событиями фиктивными работами.
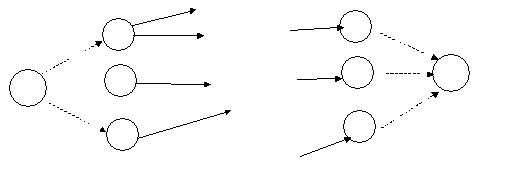
Правило 2. В сетевом графике не должно быть замкнутых путей. Замкнутым называется такой путь, который соединяет событие с самим же собой.
Отсутствие замкнутого пути необходимо для того, чтобы не произошло «зацикливание» алгоритма расчета параметров сетевого графика. В правильно организованном сетевом графике замкнутых циклов не будет тоже, так как в этом случае придется признать, что существует цикл работ, который приведет опять к тому же событию, с которого он и начинался, что будет говорить о его нерациональности. Но в проекте, совмещенным с НИОКР, могут существовать замкнутые пути в том случае, если это связано с повторным выполнением некоторых действий, например в случае неудачного эксперимента. Правило 3. Если две или более работы начинаются с одного и того же предыдущего события и заканчиваются одним и тем же последующим событием, то изображение этих работ на сетевом графике должно происходить с введением дополнительного события и связкой его с последующим событием фиктивной работой.
В противном случае образуется неопределенность относительно работ, которые исходят из одного и того же события i и заканчиваются одним и тем же событием j. Эта неопределенность касается как обозначения этих работ (непонятно, какая из работ (i;j) имеется в виду), так и неопределенности, возникающей при автоматическом расчете параметров сетевого графика. Теперь можно ввести понятие критического пути. Критический путь Lкр – это путь наибольшей длины, соединяющий начальное и конечное событие в сетевом графике. Традиция требует изображать критический путь в виде красной линии. Альтернативный способ – отображение критического пути жирной или штрихпунктирной линией. Критический путь равен продолжительности времени выполнения проекта. Планирование инновационного проекта на основе сетевого графика: расчет раннего и позднего времени свершения события, резерва времени свершения события
В методе критического пути предполагалось, что время выполнения работ нам известно. На практике, и это характерно для инновационного проекта, сроки заданы вероятностными величинами. Можно строить некоторые предположения о времени выполнения каждой работы, но нельзя предусмотреть все возможные трудности или задержки выполнения. Для управления проектом с вероятностным временем выполнения работ наиболее широкое применение получил метод анализа и оценки программ (проектов) – метод PERT, рассчитанный на использование вероятностных оценок времени выполнения работ, предусматриваемых проектом. Для каждой работы вводят три оценки: * оптимистическое время a – наименьшее возможное время выполнения работы; * пессимистическое время b – наибольшее возможное время выполнения работы; * наиболее вероятное время m – ожидаемое время выполнения работы в нормальных условиях. По a, b и m находят ожидаемое время выполнения работы:
и дисперсию ожидаемой продолжительности t:
Используя значения t, найдем критический путь сетевого графика. Распределение времени T завершения проекта является нормальным со средним E(T), равным 2 сумме ожидаемых значений времени работ на критическом пути, и дисперсией d (T), равной сумме дисперсий работ критического пути, если времена выполнения каждой из работ можно считать независимыми друг от друга. Тогда мы можем рассчитывать вероятность завершения проекта в установленный срок To:
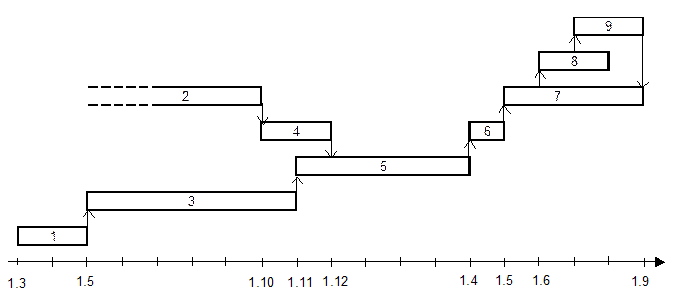
где Рассмотрим пример: Инновационный проект состоит из девяти основных работ:
Необходимо найти срок завершения проекта. Чему равно стандартное отклонение времени завершения проекта? Какова вероятность того, что выполнение проекта займет не более 25 рабочих дней? Ожидаемое время выполнения работы
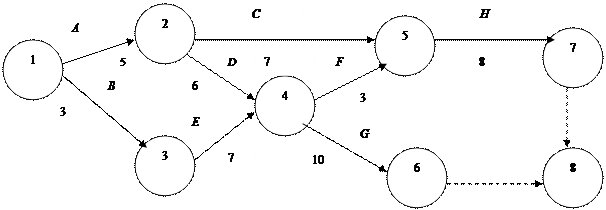
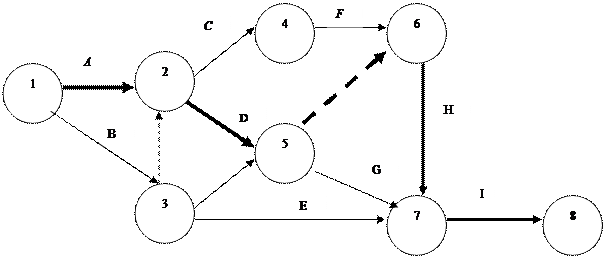
Построим сетевой график с указанием ожидаемой продолжительности каждой работы. Найдем критический путь и рассчитаем обычным способом ожидаемый срок выполнения проекта (график 3).
График 3
Расчеты
Дисперсия ожидаемого времени выполнения проекта равна сумме дисперсий критических работ.
Тогда стандартное отклонение времени выполнения проекта составит:
Найдем вероятность того, что выполнение проекта займет не более To = 25 дней.
21. Планирование инновационного проекта на основе сетевого графика: определение критического пути инновационного проекта; Метод критического пути (Critical Part Method – CPM) используется для управления проектами с фиксированным временем выполнения работ. Он позволяет ответить на следующие вопросы: 1. Сколько времени потребуется на выполнение всего проекта? 2. В какое время должны начинаться и заканчиваться отдельные работы? 3. Какие работы являются критическими и должны быть выполнены в точно определенное графиком время, чтобы не сорвать установленные сроки выполнения проекта в целом? 4. На какое время можно отложить выполнение некритических работ, чтобы они не повлияли на сроки выполнения проекта? Самый продолжительный путь сетевого графика от исходного события к завершающему называется критическим. Все события и работы критического пути также называются критическими. Продолжительность критического пути и определяет срок выполнения проекта. Критических путей на сетевом графике может быть несколько. Рассмотрим основные временные параметры сетевых графиков. Обозначим t (i;j) – продолжительность работы с начальным событием i и конечным событием j. Ранний срок tр (j) свершения события j – это самый ранний момент, к которому завершаются все работы, предшествующие этому событию. Правило вычисления:
tр (j) = max { tр (i) + t (i;j) }, где максимум берется по всем событиям i, непосредственно предшествующим событию j (соединены стрелками). Поздний срок tп (i) свершения события i – это такой предельный момент, после которого остается ровно столько времени, сколько необходимо для выполнения для выполнения всех работ, следующих за этим событием. Правило вычисления:
tп (i) = min { tп (j) – t (i;j) },
где минимум берется по всем событиям j, непосредственно следующим за событием i. Резерв R(i) события i показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока наступления завершающего события:
R(i) = tп(i) – tр(i).
Критические события резервов не имеют. Иногда при расчетах сетевого графика для удобства каждую фигуру, изображающую событие, делят на четыре сектора, где наносятся основные данные и расчетные показатели:
Рассмотрим пример планирования инновационного проекта, используя метод критического пути. Имеются следующие данные:
Необходимо найти критический путь. Сколько времени потребуется для завершения проекта? Можно ли отложить выполнение работы D без отсрочки завершения проекта в целом? На сколько недель можно отложить выполнение работы C без отсрочки завершения проекта в целом? Строим сетевой график (график 1):
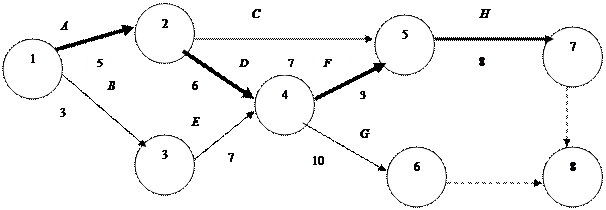
График 1 Фиктивные работы (6;8) и (7;8) введены для того, чтобы было одно завершающее событие. Расчеты Первый этап При вычислении tр(i) перемещаемся по сетевому графику от исходного события 1 к завершающему событию 8 tр (1) = 0. В событие 2 входит только одна работа. tр (2) = tр (1) + t (1;2) = 0+5 =5 Аналогично tр (3) = tр (1) + t (1;3) = 0+3 =3; В событие 4 входят 2 работы: tр (4) = max { tр (2) + t (2;4), tр (3) + t (3;4) } = max { 5 + 6, 3 + 7} = max {11, 10} = 11; tр (5) = max { tр (2) + t (2;5), tр (4) + t (4;5) } = max { 5 + 7, 11 + 3} = max {12, 14} = 14; tр (6) = tр (4) + t (4;6) = 11 + 10 = 21; tр (7) = tр (5) + t (5;7) = 14+8 =22; tр (8) = max { tр (7) + t (7;8), tр (6) + t (6;8) } = max { 22 + 0, 21 + 0} = max {22, 21} = 22; t критическое = 22. Второй этап. При вычислении tп (i) перемещаемся от завершающего события 8 к исходному 1 по сетевому графику против стрелок tп (8) = tр (8) = 22. Далее рассматриваем непосредственно предшествующее событие 7, из которого выходит только одна работа (7;8): tп (7) = tп (8) – t (7;8) = 22 – 0 = 22. Аналогично: tп (6) = tп (8) – t (6;8) = 22 – 0 = 22; tп (5) = tп (7) – t (5;7) = 22 – 8 = 14; Из события 4 выходят две работы: (4;5) и (4;6). Поэтому определяем tп (4) по каждой из этих работ: tп (4) = min { tп (5) – t (4;5), tп (6) – t (4;6) } = min { 14 – 3, 22 – 10} = min {11, 12} = 11; tп (3) = tп (4) – t (3;4) = 11 – 7 = 4; tп (2) = min { tп (5) – t (2;5), tп (4) – t (2;4) } = min { 14 – 7, 11 – 6} = min {7, 5} = 5; tп (1) = min { tп (2) – t (1;2), tп (3) – t (1;3) } = min { 5 – 4, 4 – 3} = min {0, 1} = 0. Третий этап Вычисляем R (i) = tп (i) – tр (i) – резерв времени события I, т.е. из чисел, полученных на втором этапе вычитаем числа, полученные на первом этапе. Четвертый этап У критических событий резерв времени равен нулю, так как ранние и поздние сроки их свершения совпадают. Критические события 1, 2, 4, 5, 7, 8 и определяют критический путь 1–2–4–5–7–8, который на сетевом графике обозначается двумя чертами, штрих-пунктирной или жирной линией (график 2). Для завершения проекта потребуется 22 недели. Работа D = (2;4) расположена на критическом пути. Поэтому ее нельзя отложить без отсрочки завершения проекта в целом. Работа С = (2;5) не расположена на критическом пути, ее можно задержать на tп (5) – tр (2) – t (2;5) = 14 – 5 – 7 = 2 (недели).
График 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1798; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.013 с.) |

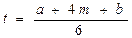
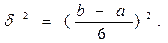
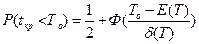 ,
,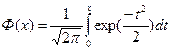 – функция Лапласа. Значение функции Лапласа находится по таблице Ф( – х)= – Ф(х).
– функция Лапласа. Значение функции Лапласа находится по таблице Ф( – х)= – Ф(х).
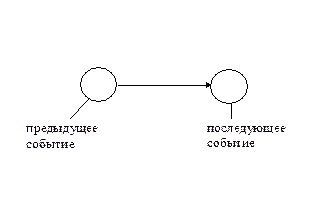
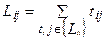 ,
,

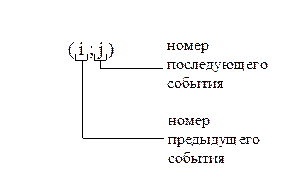
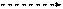
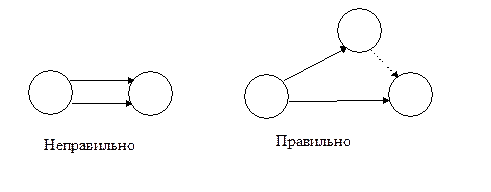
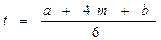 , дисперсия ожидаемой продолжительности t:
, дисперсия ожидаемой продолжительности t: 
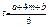
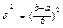
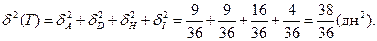
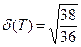
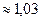 дн.
дн.