
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение (произведение) событий.Содержание книги
Поиск на нашем сайте
Пересечением или произведением событий А и В называется событие С, которое происходит тогда и только тогда, когда происходит событие А и происходит событие В вместе.
2) производится 2 выстрела по мишени
Пересечением n событий Опыт: 3 выстрела
4. Объединение (сумма) событий. Объединение (сумма) обозначается
2) 2 выстрела по мишени
Объединением (суммой) n событий Опыт: 5 выстрелов по мишени
Несовместные события. Событие А и событие В называются несовместными, если их пересечение есть несовместное событие:
Пример: Бросается игральный кубик. Рассмотрим события: А1 – число очков делится на 3 А2 – число очков делится на 5 А3 – число очков делится на 2 Не являются группой попарно несовместных событий, т.к. Полная группа событий. Говорят, что события 1) Они попарно несовместны: 2) Их объединение – есть событие достоверное:
Опыт: 2 выстрела по мишени А1 – хотя бы одно попадание А2 - хотя бы один промах е – количество дырок в мишени
Опыт: бросание двух монет А1 – появление двух гербов А2 – появление двух цифр е – появление герба или цифры
§5. Аксиомы теории вероятностей.
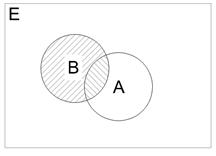
Поле событий. Пусть введено некоторое пространство элементарных событий Е, некоторое подмножество А из Е мы называем событием. Среди множества всех подмножеств пространства Е выделим такой класс К подмножеств пространства, который обладает следующими свойствами:
1) класс К в качестве элементов содержит достоверное и невозможное событие: 2) если 3) если события Такой класс К подмножеств пространства Е называется аддитивным классом. Аддитивный класс К подмножеств А из Е мы будем называть полем событий. Пример. 1) опыт: бросается игральный кубик
В этом случае под событием мы понимаем любое подмножество пространства Е. Поэтому поле событий К в случае дискретного пространства Е есть множество всех подмножеств пространства Е.
Все эти события составляют поле событий. 1. 2. 3. 2) точка случайным образом брошена на отрезок [0;1] и наблюдается 2 события: А1 – попадание точки в промежуток [0;½) A2 – попадание точки в промежуток [½;1]
Под событием понимаем то, что имеет длину. 1. 2.
3.
Аксиомы. Пусть задано пространство элементарных событий Е и поле событий К на этом пространстве. Числовая функция Р (А), 1) 2) вероятность достоверного события является единицей, Р (Е)=1 3) аксиома сложения вероятностей: если Вероятностное пространство. Говорят, что имеется вероятностная (математическая) модель случайного опыта, если построены: 1) пространство элементарных событий Е 2) поле событий К 3) распределение вероятностей на поле событий К, т.е. для каждого события А из поля событий К задана вероятность Р (А) Тройка объектов (Е, К, Р) называется вероятностным пространством (моделью) данного случайного опыта. Если Е – дискретное, то (Е, К, Р) называется дискретным. Если Е – непрерывное, то (Е, К, Р) называется непрерывным.
§6. Классическая вероятностная модель.
Вероятностная модель называется классической, если выполнены следующие 2 условия: 1) пространство элементарных событий – дискретное конечное, состоит из n элементарных событий Е ={ e1, e2, …, en }
2)
Вероятностное пространство определяется так: для заданного пространства Е поле событий К - есть множество всех подмножеств из Е, а вероятности Р (А) для любого события А из К выражаются через вероятности элементарных событий. Пусть По аксиоме 3:
§7. Геометрические вероятности.
Классическая модель: дискретная вероятностная модель Геометрическая модель: непрерывная вероятностная модель (Е, К, Р) Е – непрерывное пространство, множество точек области на плоскости К ={ A } А из Е: А – длина; А – площадь; А – объём
Наудачу бросается точка, наблюдается событие: попадание точки в область А. «Наудачу» означает: вероятность события А зависит от площади А, не зависит от её формы и положения Е.
§8. Теорема о сложении вероятностей.
(Не путать с аксиомой о сложении вероятностей). Теорема. Задано вероятностное пространство (Е, К, Р), есть события А, В
По аксиоме 3:
Вычитая из 1-го равенства 2-е получим ч.т.д. Замечание: из аксиомы 3 следует, что если события
§9. Условные вероятности.
Пример. Три раза бросается монета. Результат: цифра или герб.
n =8 A – герб выпал один раз;
Пусть в результате опыта произошло событие В. Число выпавших гербов – нечётно.
Тогда, если В произошло, Рассмотрим более общую ситуацию: пусть некоторому случайному опыту соответствует классическая вероятностная модель.
r элементарных событий входит и в А и в В. Найдём вероятность события А при условии, что произошло В. Если В произошло, то его вероятность равна 1, то Событие А происходит, если происходит элементарное событие, принадлежащее пересечению, их всего r.
Определение: пусть задано вероятностное пространство (Е, К, Р); А, В – события. Если
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.119.163 (0.01 с.) |


 1)
1)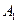 - попадание при первом выстреле
- попадание при первом выстреле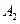 - попадание при втором выстреле
- попадание при втором выстреле - попадание при обоих выстрелах
- попадание при обоих выстрелах называется такое событие, которое происходит тогда и только тогда, когда одновременно происходит каждое из этих событий:
называется такое событие, которое происходит тогда и только тогда, когда одновременно происходит каждое из этих событий:  .
. - промах при i -м выстреле (i =1, 2, 3)
- промах при i -м выстреле (i =1, 2, 3) - в мишени нет пробоев
- в мишени нет пробоев - событие С, которое происходит тогда и только тогда, когда происходит или событие А, или событие В, или оба события сразу.
- событие С, которое происходит тогда и только тогда, когда происходит или событие А, или событие В, или оба события сразу. 1)
1) - попадание или при первом, или при втором выстреле, или оба попадания
- попадание или при первом, или при втором выстреле, или оба попадания называется такое событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий
называется такое событие, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий  - не более трёх попаданий
- не более трёх попаданий - не менее четырёх попаданий
- не менее четырёх попаданий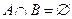
 и
и  - несовместные
- несовместные
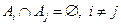 .
.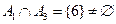


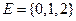

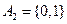
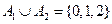

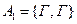


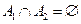


 (в конечном или счётном числе) принадлежат классу К, то их объединение или пересечение в конечном или счётном числе также принадлежит классу К.
(в конечном или счётном числе) принадлежат классу К, то их объединение или пересечение в конечном или счётном числе также принадлежит классу К. - дискретное пространство элементарных событий.
- дискретное пространство элементарных событий.
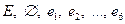



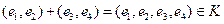

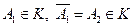

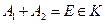

 называется вероятностью, если выполнены следующие аксиомы:
называется вероятностью, если выполнены следующие аксиомы: ставится в соответствие неотрицательное число
ставится в соответствие неотрицательное число 
 )
)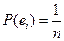 - вероятности всех элементарных событий равны
- вероятности всех элементарных событий равны


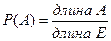 ;
; ;
; .
. Эти вероятностные пространства служат моделью задач такого типа:
Эти вероятностные пространства служат моделью задач такого типа: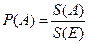
 Е.
Е.






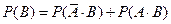




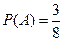

 .
. , n элементарных событий
, n элементарных событий

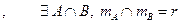
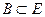

 .
.
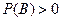 , то условной вероятностью события А при условии, что событие В произошло, называется отношение
, то условной вероятностью события А при условии, что событие В произошло, называется отношение 



