
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функция от случайных величинСодержание книги
Поиск на нашем сайте
Пусть Пусть
При этом, если в верхней строке ряда распределения появляются одинаковые значения Пример 9. Случайная величина ξ имеет ряд распределения:
Найти закон распределения случайной величины m Решение. Составим ряд распределения случайной величины
Объединив первый и пятый, второй и четвертый столбцы, получим:
Ряд распределения случайной величины
Пусть
Пример 10. Пусть случайная величина
Найти распределение случайной величины m Решение. В данном случае
Очевидно, что при
Выведем более удобные формулы для вычисления функции Теорема. Пусть
где Тогда плотность распределения случайной величины
где Доказательство. Пусть
Продифференцировав последнее равенство, получаем
Пусть
Продифференцировав последнее равенство, получаем
Учитывая свойства модуля, равенства (5.5.3) и (5.5.4) объединим в одно
что совпадает с (5.5.2). n
Пример 11. Случайная величина m Решение. Функция
Интервал
Следствие из теоремы. Если
где Пример 12. Случайная величина
m Решение. Функция
Глава 6. Числовые характеристики случайных величин
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.01 с.) |

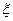 — случайная величина. Пусть задана функция
— случайная величина. Пусть задана функция 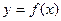 . Каждому элементарному исходу
. Каждому элементарному исходу  поставим в соответствие число
поставим в соответствие число  по формуле
по формуле  . Тем самым получим случайную величину
. Тем самым получим случайную величину 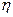 , называемую функцией
, называемую функцией  от случайной величины
от случайной величины  также является дискретной случайной величиной, поскольку она не может принимать больше значений, чем случайная величина
также является дискретной случайной величиной, поскольку она не может принимать больше значений, чем случайная величина 


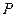



 , то соответствующие столбцы необходимо объединить в один, приписав им суммарную вероятность.
, то соответствующие столбцы необходимо объединить в один, приписав им суммарную вероятность. .
. :
:
 . Пусть случайная величина
. Пусть случайная величина  . Тогда
. Тогда . (5.5.1)
. (5.5.1) .
. .
. . Согласно (5.5.1), получим
. Согласно (5.5.1), получим .
. , функция распределения равна нулю, т.е.
, функция распределения равна нулю, т.е.  . При
. При  область
область  совпадает с областью
совпадает с областью  . Отсюда получаем
. Отсюда получаем . l
. l , где
, где  .
. ,
, .
. , (5.5.2)
, (5.5.2) — функция, обратная по отношению к функции
— функция, обратная по отношению к функции  .
. . (5.5.3)
. (5.5.3) и, следовательно,
и, следовательно,  . Отсюда получаем:
. Отсюда получаем:
 . (5.5.4)
. (5.5.4) . Найти закон распределения случайной величины
. Найти закон распределения случайной величины  .
. в интервале
в интервале 
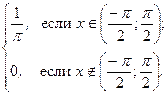








 , в котором лежат значения случайной величины
, в котором лежат значения случайной величины  для
для  . l
. l ) имеет обратная функция:
) имеет обратная функция: , (5.5.5)
, (5.5.5) — значения обратной функции для данного
— значения обратной функции для данного  .
. немонотонная в интервале
немонотонная в интервале 


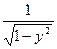


 . l
. l


