
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия. Моменты высших порядковСодержание книги
Поиск на нашем сайте
Определение. Моментом k -го порядка называется выражение, вычисляемое по формулам: а) для дискретной случайной величины:
б) для непрерывной случайной величины:
Для существования момента к-ого порядка необходимо: а) для дискретной случайной величины — абсолютная сходимость ряда
б) для непрерывной случайной величины — абсолютная сходимость интеграла
Поскольку
Определение. Момент k -го порядка величины Особую роль играет второй центральный момент, который называется дисперсией и обозначается Определение. Дисперсией случайной величины
Свойства дисперсии. 1. Дисперсия постоянной величины равна нулю, т.е.
2. Дисперсия является неотрицательной величиной, т.е. 3. Для любых действительных чисел
Доказательство. Из свойства 2 математического ожидания получаем:
n 4. Доказательство. Используя определение дисперсии и свойства 2 и 3 математического ожидания, получаем:
n 5. Если
Доказательство. Если
n Очевидно, что дисперсия
Определение. Средним квадратичным отклонением случайной величины ξ называется выражение, вычисляемое по формуле:
Пример 12. Найти дисперсию случайной величины
m Решение. Используя определение дисперсии
Пример 13. Найти дисперсию случайной величины
m Решение. Используя определение дисперсии
Делаем замену
Пример 14. При условии примера 11 найти дисперсию случайной величины m Решение. Рассмотрим 1 способ нахождения дисперсии, используя ряд распределения случайной величины
и свойство 4 дисперсии, получим:
Напомним, что математическое ожидание Перейдем ко второму способу нахождения математического ожидания случайной величины
Глава 7. Элементы математической статистики
Основные понятия и основные задачи математической статистики
В математической статистике исследуются способы получения выводов на основе эмпирических (опытных) данных. Основными понятиями математической статистики являются: генеральная совокупность, выборка, теоретическая функция распределения. Определение. Генеральной совокупностью называются все возможные результаты наблюдений, которые могут быть сделаны при данном комплексе условий. В некоторых задачах генеральную совокупность рассматривают как случайную величину Определение. Выборочной совокупностью (выборкой) называется множество результатов, случайно отобранных из генеральной совокупности. Выборка должна быть репрезентативной, т.е. правильно отражать пропорции генеральной совокупности. Это достигается случайностью отбора, когда все объекты генеральной совокупности имеют одинаковую вероятность быть отобранными. Определение. Число объектов в совокупности (генеральной или выборочной) называется ее объемом. Объем генеральной совокупности обозначим символом
Заметим, что сам процесс выбора можно осуществлять разными способами: выбрав объект и определив его значение, изымать объект и не допускать к последующим испытаниям (выборка без возвращения); после определения его значения объект возвращается в генеральную совокупность (выборка с возвращением). Очевидно, что при достаточно большом объеме генеральной совокупности исчезает различие между выборками с возвращением и без возвращения. Будем рассматривать случай бесконечно большого объема генеральной совокупности. Основные задачи математической статистики: 1. Оценка значения неизвестной вероятности случайного события; 2. Определение неизвестной теоретической функции распределения; 3. Определение неизвестных параметров распределения теоретической функции распределения; 4. Проверка статистических гипотез; 5. Оценка зависимости.
§2. Простейшие статистические преобразования
Для обоснованных статистических выводов необходимо иметь выборку достаточно большого объема Определение. Статистикой
Как функция от случайного вектора Определение. Вариационным рядом Очевидно, что данное преобразование не приводит к потере информации относительно теоретической функции распределения. Для величин Определение. Размахом варьирования называется разность между крайними членами вариационного ряда, т.е.
Если среди элементов выборки Определение. Значение выборки Если Определение. Отношение частоты Определение. Статистическим рядом называется расположенная по возрастанию совокупность различных вариант При наблюдении непрерывной случайной величины используют интервальный ряд. В этом случае весь возможный интервал, которому принадлежат значения выборки, разбивают на конечное число частичных интервалов и подсчитывают частоту попадания элементов выборки в каждый частичный интервал. Определение. Интервальным рядом называется упорядоченная последовательность интервалов с соответствующими им частотами или относительными частотами попадания элементов выборки в каждый из этих интервалов. Пример 1. В городе A для определения сроков гарантированного обслуживания проведено исследование величины среднего пробега автомобилей, находящихся в эксплуатации в течение двух лет. Получены следующие результаты (тыс. км.):
3,0; 25,0; 18,6; 12,1; 10,6; 18,0; 17,3; 29,1; 20,0; 18,3; 21,5; 26,7; 12,2; 14,4; 7,3; 9,1; 2,9; 5,4; 40,1; 16,8; 11,2; 9,9; 25,3; 4,2; 29,6. Составить интервальный ряд. m Решение. Очевидно, что величина среднего пробега автомобилей, находящихся в эксплуатации в течение двух лет, является непрерывной случайной величиной. Полученные данные представляют собой выборку из Возьмем число частичных интервалов
Соответствующий интервальный ряд приведен в таблице 7.1. Таблица 7.1
l
Пример 2. Наблюдается число выигрышей в мгновенной лотерее. В результате наблюдения получены следующие значения выигрышей (тыс. руб.): 0, 1, 0, 0, 5, 0, 10, 0, 1, 0, 0, 1, 5, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 5, 0, 5, 0, 0, 1, 1, 1, 5, 10, 0, 1, 1, 0, 5, 0, 0, 0, 0, 1, 0, 1, 0, 5, 0, 0, 0, 0, 1, 0. Требуется составить статистический ряд случайной величины m Решение. Случайнаявеличина Таблица 7.2
l
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.23 (0.01 с.) |

 , (6.3.1)
, (6.3.1) . (6.3.2)
. (6.3.2) , (6.3.3)
, (6.3.3) . (6.3.4)
. (6.3.4) , то из существования момента к-го порядка вытекает существование момента (к-1)-го порядка и, следовательно, всех моментов меньших порядков.
, то из существования момента к-го порядка вытекает существование момента (к-1)-го порядка и, следовательно, всех моментов меньших порядков. называется центральным моментом k -го порядка.
называется центральным моментом k -го порядка. .
.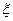 называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания:
называется математическое ожидание квадрата отклонения случайной величины от своего математического ожидания: . (6.3.5)
. (6.3.5)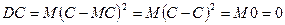 . n
. n .
.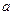 и
и  справедливо равенство
справедливо равенство .
.
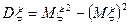 .
.
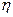 независимые случайные величины, дисперсия суммы случайных величин равна сумме дисперсий случайных величин, т.е.
независимые случайные величины, дисперсия суммы случайных величин равна сумме дисперсий случайных величин, т.е. .
. будут независимыми. Тогда, используя свойства 2-4 математического ожидания, получаем:
будут независимыми. Тогда, используя свойства 2-4 математического ожидания, получаем: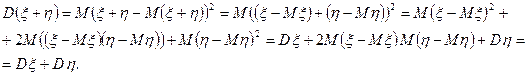
 . (6.3.6)
. (6.3.6) ):
):
 .l
.l (см. Пример 4).
(см. Пример 4). . (6.3.5)
. (6.3.5)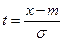 или
или 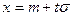 , при этом
, при этом 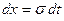 . В этом случае выражение (6.3.5) примет вид:
. В этом случае выражение (6.3.5) примет вид: l
l .
.


 было найдено в примере 12.
было найдено в примере 12. . Используя свойство 5 дисперсии случайной величины, получим:
. Используя свойство 5 дисперсии случайной величины, получим: ,
,  ,
, ,
,  ,
, ,
,  . l
. l . Примером генеральной совокупности может быть все население страны. В этой совокупности нас могут интересовать, например, возраст жителей. Другим примером генеральной совокупности являются детали, изготовленные на данном станке. Эти детали могут быть качественными и бракованными.
. Примером генеральной совокупности может быть все население страны. В этой совокупности нас могут интересовать, например, возраст жителей. Другим примером генеральной совокупности являются детали, изготовленные на данном станке. Эти детали могут быть качественными и бракованными.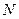 , а объем выборочной совокупности обозначим символом
, а объем выборочной совокупности обозначим символом 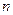 . При этом подразумевается, что
. При этом подразумевается, что  .
. называется произвольная k‑мерная функция от выборки
называется произвольная k‑мерная функция от выборки  :
:
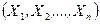 статистика
статистика 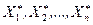 является выборка
является выборка  .
.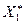 и
и 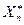 употребляют название «крайние члены вариационного ряда».
употребляют название «крайние члены вариационного ряда». . (7.2.1)
. (7.2.1)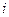 — индекс варианты, то
— индекс варианты, то 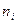 — число значений
— число значений  называется относительной частотой варианты и обозначается
называется относительной частотой варианты и обозначается  .
. , представляющих выборку
, представляющих выборку  наблюдений. Найдем сначала минимальное и максимальное значения случайной величины (т.е. крайние члены вариационного ряда):
наблюдений. Найдем сначала минимальное и максимальное значения случайной величины (т.е. крайние члены вариационного ряда):  и
и  . Размах варьирования будет равен
. Размах варьирования будет равен  .
.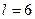 . В этом случае длина частичного интервала равна
. В этом случае длина частичного интервала равна .
.





