
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4. Схема независимых испытаний. Схема БернуллиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формула Бернулли Определение. Повторные независимые испытания называются испытаниями Бернулли, если каждое испытание имеет только два исхода, и вероятности исходов остаются неизменными для всех испытаний. Обычно эти две вероятности обозначаются через
Пространство элементарных исходов каждого отдельного испытания состоит из двух исходов 1 и 0. Очевидно, пространство элементарных исходов
Но на практике нас, как правило, интересует не порядок появления успехов в последовательности Теорема. Вероятность
где Доказательство. Событие «в
Число успехов в
Пример 1. Стрелок попадает в мишень с вероятностью a) ровно четыре раза; б) не менее трех раз. m Решение. Для решения данной задачи применим формулу (4.1.2), в которой:
а) Число успехов равно
б) Обозначим
Пример 2. Сколько испытаний с вероятностью успеха m Решение. Рассмотрим следующие события:
Для решения задачи используем формулу (4.1.2), согласно которой вероятность того, что успехов не будет (т.е. число успехов равно нулю), равна:
Используя свойство вероятности противоположного события, получаем, что вероятность того, что будет хотя бы один успех, равна:
Остается найти наименьшее целое
Решим последнее неравенство.
Разделив последнее неравенство на
Наименьшим целым числом
Пример 3. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен): а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми. m Решение. Так как противники равносильны и ничейный исход партии исключен, то вероятности выигрыша и проигрыша каждой партии одинаковы и а) Вероятность выигрыша трех партий из четырех равна:
а вероятность выигрыша пяти партий из восьми равна:
Так как б) Вероятность выигрыша не менее трех партий из четырех равна:
а вероятность выигрыша не менее пяти партий из восьми равна:
Так как
Формула Пуассона
При больших значениях числа испытаний
и не мало, и не велико. В таких случаях удобно использовать для вероятности
При
Следовательно, (4.2.2) примет вид:
а это и есть формула Пуассона.
Замечание. При выводе формулы Пуассона (4.2.3) использовалось то, что Замечание. Формула Пуассона (4.2.3) зависит от § можно воспользоваться Приложением 1; § используя функцию ПУАССОН (x;среднее;интегральная) из EXCEL; в которой аргумент x равен числу «успехов» § используя функцию dpois(k, l) из MATHCAD, в которой
Пример 4. Найти вероятность того, что среди 1460 человек ровно трое родились 29 февраля. m Решение. Вероятность того, что один конкретный человек родился 29 февраля, равна Далее находим коэффициент
Применяя (4.2.2), получаем:
Пример 5. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность того, что при 5000 выстрелах в цель попало не менее двух выстрелов. m Решение. Рассмотрим два противоположных события:
Найдем вероятность события
В рассматриваемом примере
Используя формулу Пуассона, получим
Используя свойство вероятности противоположного события, получим
Формулы Муавра – Лапласа
Если в схеме Бернулли то следует применять формулы Муавра – Лапласа: локальную или интегральную. Локальная теорема Муавра‑Лапласа (без доказательства). Если в схеме Бернулли
Значения функции § можно воспользоваться Приложением 2; § используя функцию НОРМРАСП(x;среднее;стандартное_откл;интегральная) из EXCEL; в которой «среднее» необходимо положить равным 0, аргумент «стандартное_откл» необходимо положить равным 1, аргумент «интегральная» должен равняться 0. § используя функцию dnorm(x, mu, sigma) из MATHCAD, в которой Очевидно, что функция Интегральная теорема Муавра‑Лапласа (без доказательства). Если в схеме Бернулли число испытаний
Функция § можно воспользоваться Приложением 3; § используя функцию НОРМРАСП(x;среднее;стандартное_откл;интегральная) из EXCEL; в которой «среднее» необходимо положить равным 0, аргумент «стандартное_откл» необходимо положить равным 1, аргумент «интегральная» должен равняться 1. § используя функцию pnorm(x, mu, sigma) из MATHCAD, в которой Функцию Замечание. Нарядус функцией
Для нее справедливо равенство
Пример 6. Симметричную монету бросают 400 раз. Определить вероятность появления герба: а) от 185 до 210 раз; б) ровно 200 раз; в) не менее 200 раз. m Решение. Для решения задачи применим локальную и интегральную теоремы Муавра‑Лапласа, для которых
а) Используя интегральную теорему Муавра‑Лапласа, получим
б) Используя локальную теорему Муавра‑Лапласа, получим
в) Используя интегральную теорему Муавра‑Лапласа, получим
Пример 7. Команда состоит из 10 отличных и 15 хороших стрелков. Каждый стрелок производит по своей мишени 5 независимых выстрелов. Отличный стрелок при каждом выстреле попадает в цель с вероятностью 0,9, хороший — с вероятностью 0,8. Определить вероятность того, что общее число попаданий будет не менее 110. m Решение. Найдем вероятность попадания при одном выстреле для произвольного стрелка. Для этого воспользуемся формулой полной вероятности. Пусть искомое событие
Очевидно, что:
Отсюда получаем:
Заметим, что общее число выстрелов
Теперь найдем вероятность
Пример 8. Вероятность попадания в мишень при одном выстреле m Решение. По условию задачи
Заметим, что мы использовали то, что при больших значениях Далее получаем
Используя Приложение 3 находим, что
Решая последнее уравнение для натуральных значений
|
|||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 1287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.46.108 (0.012 с.) |

 и
и  , исход с вероятностью
, исход с вероятностью  . (4.1.1)
. (4.1.1)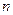 испытаний Бернулли содержит
испытаний Бернулли содержит  последовательностей из
последовательностей из  равна:
равна: .
.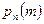 того, что в
того, что в  , вычисляется по формуле
, вычисляется по формуле , (4.1.2)
, (4.1.2) » содержит столько элементарных исходов, сколько существует способов размещения
» содержит столько элементарных исходов, сколько существует способов размещения  . А так как вероятность конкретной последовательности, содержащей
. А так как вероятность конкретной последовательности, содержащей  , то в итоге получаем:
, то в итоге получаем: , тогда
, тогда  . Очевидно, что
. Очевидно, что  . Отсюда следует, что
. Отсюда следует, что .
. . Найти вероятность того, что в результате пяти независимых выстрелов стрелок попадает:
. Найти вероятность того, что в результате пяти независимых выстрелов стрелок попадает: .
. . Таким образом, искомая вероятность:
. Таким образом, искомая вероятность: .
. — вероятность попадания не менее трех раз из пяти.
— вероятность попадания не менее трех раз из пяти.
 . l
. l нужно произвести, чтобы вероятность хотя бы одного успеха была не меньше 0,5?
нужно произвести, чтобы вероятность хотя бы одного успеха была не меньше 0,5? — в схеме Бернулли наблюдался хотя бы один успех;
— в схеме Бернулли наблюдался хотя бы один успех; — в схеме Бернулли не наблюдалось ни одного успеха.
— в схеме Бернулли не наблюдалось ни одного успеха. .
. .
. .
.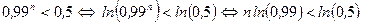 .
. , получим
, получим .
. . l
. l .
. ,
, .
.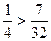 , то вероятнее выиграть три партии из четырех.
, то вероятнее выиграть три партии из четырех.

 , то вероятнее выиграть не менее пяти партий из восьми. l
, то вероятнее выиграть не менее пяти партий из восьми. l . Пусть число испытаний
. Пусть число испытаний  (4.2.1)
(4.2.1)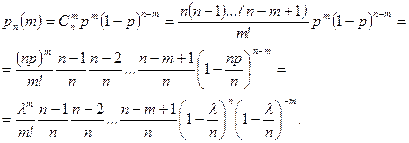 (4.2.2)
(4.2.2) и сделанных выше допущениях очевидны следующие приближения:
и сделанных выше допущениях очевидны следующие приближения: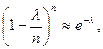
 ,
,  .
. , (4.2.3)
, (4.2.3) . Значения функции (4.2.2) можно определить следующими способами:
. Значения функции (4.2.2) можно определить следующими способами: и
и  .
. , т.к. 29 февраля бывает ровно 1 раз в 4 года.
, т.к. 29 февраля бывает ровно 1 раз в 4 года. .
. . l
. l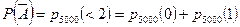 .
.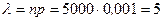 .
. .
. . l
. l ,
,  , (4.3.1)
, (4.3.1) (4.3.2)
(4.3.2) , которую называют плотностью нормального распределения с параметрами
, которую называют плотностью нормального распределения с параметрами 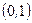 , можно найти одним из следующих способов:
, можно найти одним из следующих способов: и
и  .
. нужно воспользоваться равенством
нужно воспользоваться равенством 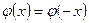 .
. того, что число успехов
того, что число успехов  до
до  , справедлива интегральная теорема Муавра‑Лапласа:
, справедлива интегральная теорема Муавра‑Лапласа: (4.3.3)
(4.3.3)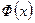 , определенная формулой (4.3.3), называется функцией распределения нормального распределения с параметрами
, определенная формулой (4.3.3), называется функцией распределения нормального распределения с параметрами  .
. . (4.3.4)
. (4.3.4) ; она связана с функцией
; она связана с функцией  . (4.3.5)
. (4.3.5) , т.к. монету подбрасывали 400 раз,
, т.к. монету подбрасывали 400 раз, 
 ;
;
 . l
. l — стреляет отличный стрелок;
— стреляет отличный стрелок; — стреляет хороший стрелок.
— стреляет хороший стрелок. ,
,  ,
,  ,
, 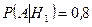 .
. ,
,  .
. .
. того, что при 125 выстрелах число попаданий будет не менее 110. Для этого применим интегральную теорему Муавра‑Лапласа:
того, что при 125 выстрелах число попаданий будет не менее 110. Для этого применим интегральную теорему Муавра‑Лапласа: ,
,  ,
, . l
. l . Найти наименьшее число выстрелов, которое надо произвести по мишени, чтобы с вероятностью 0,95 число попаданий было не менее 70.
. Найти наименьшее число выстрелов, которое надо произвести по мишени, чтобы с вероятностью 0,95 число попаданий было не менее 70. . Для вычисления
. Для вычисления  применим интегральную теорему Муавра – Лапласа:
применим интегральную теорему Муавра – Лапласа:

 .
. .
. .
.


