
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Бернулли для потока реальной жидкостиСодержание книги
Поиск на нашем сайте
При движении реальных жидкостей начинают действовать силы внутреннего трения в потоке жидкости и силы трения о стенки трубы. На преодоление гидравлических сопротивлений расходуется часть энергии потока. Поэтому общее количество энергии потока по длине трубопровода будет уменьшаться вследствие перехода потенциальной энергии в потерянную энергию, рассеиваемую в окружающую среду. Потерянная энергия учитывается величиной потерянного гидравлического потока h п. Поэтому для реальной жидкости уравнение Бернулли приобретает следующий вид:
где
h п – потери гидравлического напора при переходе жидкости из сечения I в сечение II (8). Коэффициенты а 1 и а 2, называемые коэффициентами Кориолиса или коэффициентами кинетической энергии, учитывают влияние неравномерности распределения скоростей движения слоев по поперечному сечению потока на его кинетическую энергию. Для ламинарного движения а @2. Для турбулентного режима а @1,05¸1,1. Потери гидравлического напора h п возникают в следствие сил трения о стенки трубы и из-за локальной потери энергии потоком жидкости при преодолении местных сопротивлений (сужения, поворотов и т.д.). По законам термодинамики эта энергия рассеивается в окружающую среду.
Практические приложения уравнения Бернулли
Расходомер Вентури
В расходомере Вентури (рис. 3.4) искусственно создается перепад давления, измерив который можно рассчитать расход жидкости.
Рис. 3.4. Схема расходомера Вентури Для реального потока жидкости с достаточной для большинства технических измерений и исследований точностью в уравнении Бернулли (3.4) величины а 1 и а 2 можно принять равными единице. Для двух сечений горизонтального расходомера имеем:
На участке трубки 1–2 потери гидравлического напора можно принять равными нулю h п,1–2 = 0.
Тогда:
Величина Разность потенциальных энергий жидкости в сечениях I и II равна E 1 – E 2 = D h и измеряется с помощью пьезометров (рис. 3.4).
Следовательно:
(W 22 – W 12)/(2× g) = D h. (3.6)
В соответствии с законом сохранения массы имеем:
W 1 × S 1 = W 2 × S 2, (3.7) где S 1, S 2 – площади поперечных сечений I и II трубки Вентури С учетом (3.7) получим:
W 1 = W 2 × Подставив (3.6) в (3.4), найдем:
Расход жидкости равен Q:
где K т – постоянная расходомера Вентури:
K т =
Выражение для расхода жидкости можно получить и так:
где K т = Расходомерная диафрагма
Более простым по сравнению с предыдущим является метод измерения расхода жидкости с помощью измерительной шайбы или диафрагмы (рис. 3.5). Расход жидкости определяется по уравнениям (3.9 и 3.10).
Трубка Пито – Прандтля
Простейшим прибором для измерения скорости движущейся жидкости или газа является трубка Пито – Прандтля. Конструкция ее представлена на рис. 3.6. Она состоит из трубок прямой (1) и согнутой под прямым углом (2). Запишем уравнение Бернулли для сечений I и II.
где Р 1, Р 2 – гидростатические давления жидкости в сечениях I и II, g – ускорение свободного падения, м/с2.
В сечении II скорость жидкости или газа перед изогнутым концом трубки равна нулю W 2 = 0, т.к. здесь жидкость тормозится. Тогда из (3.11) получим:
где E 1, E 2 – потенциальные энергии жидкости в сечениях I и II. Поскольку E 2 – E 1 = D h, получим:
где D h – разность высот в пьезометрических трубках. Отсюда найдем скорость жидкости или газа W 1 в трубопроводе:
ЛАБОРАТОРНАЯ РАБОТА № 3
ИССЛЕДОВАНИЕ ПРЕОБРАЗОВАНИЯ ФОРМ ЭНЕРГИИ СТРУИ Цель работы: повышение уровня знаний о движении жидкости в трубопроводах, о преобразовании кинетической и потенциальной форм энергии в них.
Задачи работы 1. Убедиться на опыте в переходе кинетической энергии потока в потенциальную и обратно. 2. Оценить полноту преобразования форм энергии и связанные с этим гидравлические сопротивления. 3. Вычислить параметры преобразования форм энергии на отдельных участках экспериментального трубопровода и сравнивать результаты с экспериментальными данными.
Теоретические основы работы Для реальной жидкости, уравнение Бернулли имеет вид
где r – плотность жидкости, кг/м3; V – скорость движения жидкости, м/с; Р – статическое давление, Па; h – нивелировочная высота жидкостной струи над уровнем её отсчета, м; g – ускорение силы тяжести, м/с2; D Р n – потери давления, на рассматриваемом участке, Па; a – коэффициент кинетической энергии (коэффициент Кариолиса), определяемый различиями средних по сечению местных скоростей течения жидкости. Уравнение Бернулли называют также основным уравнением гидродинамики, его физический смысл следующий: «Давление жидкости, текущей по трубе, больше там, где скорость движения жидкости меньше, и обратно: давление меньше там, где скорость движения жидкости больше» [3, с. 350-352]. Этот закон назван по имени швейцарского физика и математика Даниила Бернулли (1700-1782). Часто уравнение Бернулли записывают в несколько измененном виде
где
h – нивелировочная высота струи над нулевым уровнем отсчета; Н – полная гидравлическая высота (полное давление в жид- Это выражение читается так: «Полная гидравлическая высота столба жидкости, характеризующего его полное давление, складывается из суммы скоростной, статической и нивелировочной высоты и не изменяется при течении идеальной жидкости». Полная механическая энергия жидкости не исчезает, а лишь перераспределяется между указанными тремя составляющими. Если скоростной напор потока
В горизонтально расположенной трубе, во всех сечениях которой нивелировочная высота одинакова, она суммируется с константой в правой части уравнения (3.1). В этом случае разность полного и статического давлений равна динамическому напору, т.e.
P * – P о.=
Все три составляющие полного давления равноправны в его создании. В частности, машины для повышения давления (насосы) могут увеличивать любую из этих составляющих.
|
||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.58.68 (0.007 с.) |

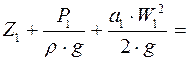
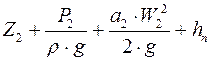 , (3.4)
, (3.4) ,
,  – удельные кинетические энергии потока в первом и втором сечениях;
– удельные кинетические энергии потока в первом и втором сечениях; ,
,  – удельные потенциальные энергии положения;
– удельные потенциальные энергии положения;

 . (3.5)
. (3.5)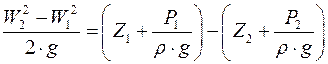 .
. = Е 1 представляет собой потенциальную энергию E 1 положения единичной массы жидкости и ее давления, аналогично
= Е 1 представляет собой потенциальную энергию E 1 положения единичной массы жидкости и ее давления, аналогично  = E 2.
= E 2. или W 2 = W 1 ×
или W 2 = W 1 ×  . (3.8)
. (3.8) .
. , (3.9)
, (3.9)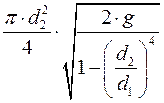 .
.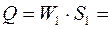
 , (3.10)
, (3.10) .
.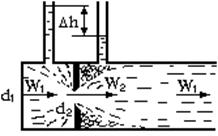 Рис. 3.5. Схема расходомерной диафрагмы
Рис. 3.5. Схема расходомерной диафрагмы
 , (3.11)
, (3.11) Рис. 3.6. Схема измерений, используемых в трубке
Пито – Прандтля
Рис. 3.6. Схема измерений, используемых в трубке
Пито – Прандтля
 ,
, , (3.12)
, (3.12) . (3.13)
. (3.13) ,
, ,
, – скоростная высота столба жидкости, являющаяся мерой скоростного напора струи жидкости, м;
– скоростная высота столба жидкости, являющаяся мерой скоростного напора струи жидкости, м; – пьезометрическая высота столба жидкости в струе, характеризующая статическое давление, м;
– пьезометрическая высота столба жидкости в струе, характеризующая статическое давление, м; перевести в статическое давление путем торможения струи, то давление в этом месте будет равно полному давлению равному
перевести в статическое давление путем торможения струи, то давление в этом месте будет равно полному давлению равному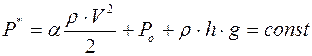 . (3.14)
. (3.14) . (3.15)
. (3.15)


