
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Физические свойства жидкостейСодержание книги Поиск на нашем сайте В.С. Ванин
Т.В. Галаган В.А. Данилов В.А. Бузуев
ГИДРАВЛИКА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО «ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
В.А. Данилов, В. Бузуев
ГИДРАВЛИКА
Рекомендовано редакционно-издательским советом ОрелГТУ в качестве учебно-методического пособия
Орел 2008 УДК 621.82(075) ББК 34.447 В17
Рецензенты:
доктор технических наук, профессор Л.C. Ушаков
кандидат технических наук, доцент кафедры «Машины и аппараты пищевых производств» Л.М. Камозин
Учебно-методическое пособие составлено в соответствии с требованиями государственных общеобразовательных стандартов высшего профессионального образования. Данное учебно-методическое пособие позволяет изучить основные разделы гидравлики и закрепить полученные знания путем проведения лабораторных работ по дисциплине «Гидравлика», а также решать практические задачи. Методика проведения экспериментальных исследований и обработки полученных гидравлических характеристик рассматриваемого технологического оборудования, обширный справочный материал позволит квалифицированно выполнить соответствующие разделы в курсовых и дипломных проектах студентов. Предназначено студентам технических и технологических направлений и специальностей вузов.
УДК 621.82(075) ББК 34.447
© ОрелГТУ, 2008 СОДЕРЖАНИЕ
ВВЕДЕНИЕ Знание основ гидравлики позволяет решать многие проблемы, встающие перед инженером любой отрасли промышленности по доставке жидкостей, газов к технологическим аппаратам. Данное учебно-методическое пособие составлено в соответствии с требованиями государственных общеобразовательных стандартов высшего профессионального образования и позволяет изучить основные разделы гидравлики и закрепить полученные знания путем проведения лабораторных работ по дисциплине «Гидравлика», а также решать практические задачи на производстве с помощью полученных знаний. Методика проведения экспериментальных исследований и обработки полученных гидравлических характеристик рассматриваемого технологического оборудования, обширный справочный материал позволит квалифицированно выполнить соответствующие разделы в курсовых и дипломных проектах студентов любой специальности. С молекулярно-кинетических позиций о строении вещества различия капельных жидкостей и газов определяются количеством химических или силовых связей молекул вещества. Если в твердом кристаллическом теле практически каждая молекула связана с соседней, то в капельной жидкости половина этих связей разорвана. В газах межмолекулярные силовые связи отсутствуют полностью. Следствием этого является то, что уменьшить эти расстояния, т.е. сжать капельную жидкость, затруднительно, а газ – относительно легко. Поэтому капельные жидкости считаются несжимаемыми, а газы – сжимаемыми. На основании этого деление сплошных сред на жидкости и газы может заменяться делением на сжимаемые и несжимаемые жидкости. При изучении законов гидравлики рассматриваются три типа капельных жидкостей: 1) идеальная жидкость – это абстрактная модель жидкости, обладающая абсолютной текучестью и неизменяемостью объема при изменении внешних условий (абсолютной несжимаемостью). Вязкость в таких жидкостях отсутствует; 2) реальные, или вязкие жидкости – это физические тела, обладающие большой подвижностью, способные изменять свой объем при изменении внешних условий и в которых возникают касательные напряжения при движении за счет внутреннего трения. Такие жидкости называют ньютоновскими; 3) неньютоновские, или реологические жидкости. Они обладают специфичными свойствами, часть из которых рассматривается далее.
Плотность
Масса единицы объема жидкости называется плотностью и обозначается через r:
r = m/V, где m - масса жидкости; V – объем жидкости. В единицах СИ плотность измеряется в кг/м3. Плотность воды при температуре 39,8 °C равна 1000 кг/м3. Вес единицы объема жидкости называется удельным весом и обозначается через g:
g= G/V.
В единицах СИ удельный вес измеряется в Н/м3. Масса и вес связаны между собой соотношением:
G = m ×g, где g – ускорение свободного падения, м/с2. Отсюда:
g=
Вязкость
Вязкостью называется свойство жидкости оказывать сопротивление усилиям, вызывающим относительное перемещение ее частиц при ламинарном течении. Различают динамическую и кинематическую вязкость. Причиной вязкостного сопротивления движению является молекулярное взаимодействие между частицами жидкости, а также взаимодействие между молекулами жидкости и движущегося в ней твердого тела. Обусловленная вязкостью сила внутреннего трения направлена в сторону, противоположную движению слоя, перемещающегося с бóльшей скоростью, и действует на этот слой. Тем самым сила внутреннего трения вызывает сопротивление движению этого слоя жидкости. Вязкость является основным отличием реальной жидкости от жидкости идеальной, которая вязкости не имеет. Первоначальные основы закона внутреннего трения между слоями жидкости даны И. Ньютоном в 1686 г. и сводятся, в частности, к следующему: 1) вязкость и сила внутреннего трения практически не зависят от давления; 2) внутреннее трение прямо пропорционально относительной скорости перемещения смежных слоев друг по другу или градиенту скорости. Под относительной скоростью в данном случае понимается приращение скорости при переходе от одного слоя «a» к другому слою «b» по нормали к направлению движения жидкости, т.е. dW/dn (рис. 1). Это приращение скорости на единицу длины по нормали к движению потока называют градиентом скорости. Всесторонние исследования распределения скорости по нормали к стенке показали, что скорость струек различна. По мере приближения исследуемого потока к стенке скорость его уменьшается. На самой поверхности стенки жидкость как бы прилипает к ней, и скорость становится равной нулю. И наоборот, по мере удаления струйки от стенки скорость ее увеличивается.
Рис. 1.1. Иллюстрация определения градиента скорости вблизи неподвижной поверхности В дальнейшем высказанное Ньютоном положение о внутреннем трении жидкости было проверено опытами крупнейшего русского ученого Н.П. Петрова (1836–1920). Математической формулировкой закона Ньютона является выражение:
T = m× F ×dW / dn, где T – сила внутреннего трения (H) или касательная сила, которую нужно прилагать, чтобы перемещать один слой жидкости относительно другого с постоянной скоростью; F – площадь соприкосновения слоев жидкости (м2); dW/dn – градиент скорости (1/сек); m – динамический коэффициент вязкости или динамическая вязкость (Па·c). В технической системе единиц динамическая вязкость измеряется в пуазах (П) или сантипуазах и связана с единицей динамической вязкости в системе СИ выражением:
1 П =0,1 Па·с.
Из закона Ньютона вытекает понятие об удельной силе внутреннего трения, или касательном напряжении:
t = T / F= m ×dW / dn.
Из последнего выражения следует, что при dW/dn =1, t=m. Следовательно, коэффициент динамической вязкости выражает силу трения T, приходящуюся на единицу поверхности F между двумя скользящими относительно друг друга слоями, когда на единице длины нормали к поверхности скольжения скорость движения изменяется на единицу скорости. В системе СГС величина m имеет размерность дина·с/см2. От названия единицы силы – дина и произошло название «динамическая вязкость». Кинематическая вязкость n определяется по следующему уравнению:
n = m / r м2/с.
В технической системе единиц кинематическая вязкость измеряется в стоксах (Ст) или сантистоксах. Соотношение единиц кинематической вязкости в технической системе единиц и в системе СИ имеет вид: 1 Ст=10-4 м2/с = 1 см2/с.
Эталоном вязкости служит дистиллированная вода, поэтому иногда вязкость измеряют в градусах Энглера. Вязкость в градусах Энглера о Е является отношением времени τ 1 истечения 200 см3 исследуемой жидкости из некоего сосуда ко времени τ истечения того же объема дистиллированной воды из того же сосуда при температуре 20 оС:
о Е= где t = 51,6 с. Переход от вязкости в градусах Энглера к кинематической вязкости в системе СИ выполняется по эмпирической формуле Убеллоде:
Вязкость капельных жидкостей значительно снижается с возрастанием температуры. Вязкость газов, наоборот, увеличивается с ее повышением. Причина различия влияния температуры на вязкость капельных жидкостей и газов обусловлена тем, что вязкость газов имеет молекулярно-кинетическую природу, а вязкость капельных жидкостей в основном зависит от сил сцепления между молекулами. Поскольку плотность газов примерно в тысячу раз меньше плотности капельных жидкостей, то их кинетическая вязкость может быть больше вязкости этих жидкостей. Справка. Мы говорим «молекулы» воды, газа, белка и т.п. Слово молекула появилось почти 350 лет назад в книге французского философа Пьера Гассенди, изданной в 1647 г. По Гассенди молекула («массочка», от латинского слова «moles» – масса) – это несколько атомов, объединенных в одну группу, сохраняющую свою целостность. По разному объединенные атомы, т.е. разные молекулы, составляют «кирпичики», из которых природа строит разнообразные тела. Молекулы всех веществ невообразимо малы. Их размеры – миллионные доли миллиметра, т.е. тысячные доли микрона. Ни в какой самый сильный оптический микроскоп невозможно разглядеть молекулы. Все то, что мы видим, что можем потрогать руками, состоит из гигантского количества молекул. В капельке воды содержится сто секстиллионов молекул – единица с 23 нулями. А на кончике комариного жала (его площадь около 10-10 мм2) могут поместиться десятки тысяч молекул воды. Молекулы состоят из атомов. Разновидностей атомов не так много: чуть более ста. Догадки об атомарном строении вещества высказывали еще в глубокой древности. Более 2000 лет назад древнегреческий философ Демокрит представлял себе мир так: «…существуют атомы и пустота. Атомы – неделимые материальные элементы, вечные, неразрушимые, непроницаемые, различаются формой, величиной, положением в пустоте; из их вихря образуются как отдельные тела, так и все бесчисленные миры». [3, стр.36–41]. Слово «атом» происходит от греческого «atomos» – неделимый. Именно это свойство атома древнегреческие философы считали самым главным. Однако они ошибались. Атом оказался делимым. Его строение впервые было описано великим физиком Эрнестом Резерфордом в 1911 году. Он пришел к поразительному выводу: атом внутри не заполнен. Почти вся его масса сосредоточена внутри центральной его части – атомном ядре, вокруг которого вращаются электроны. Атом подобен солнечной системе, уменьшенной в миллиарды миллиардов раз. Поэтому модель Резерфорда называют планетарной моделью атома. Простейшим из атомов является атом водорода, входящий в молекулу воды. Атом водорода состоит из ядра и вращающегося вокруг него по определенным орбитам электрона. Масса атома равна 1,66∙10-27 г. Диаметр атома водорода приблизительно равен 10-8 см. Эта величина соответствует одному ангстрему. Точно определить размер атома нельзя – граница его как бы размыта. Радиус ядра атома водорода примерно в сто тысяч раз меньше радиуса атома и составляет 1,3·10-13 см. Плотность вещества в ядре чрезвычайно велика. Она составляет около 2·1014 г/см3, т.е. около двухсот миллионов тонн в кубическом сантиметре. Плотность же воды равна 1 г/см3. Булавочная головка из вещества с плотностью ядра оказалась бы тяжелее стальной глыбы размером с десятиэтажное здание. Поверхностное натяжение
Всякая молекула, расположенная в глубине жидкости, притягивается своими соседками. Силы этого притяжения взаимно уравновешены и поэтому не будут заметны. Иная картина у тех молекул, которые расположены не в глубине, а в поверхностном слое жидкости. Они притягиваются снизу и со всех сторон, но не сверху, так как там находится уже не жидкость, а другая среда. В результате поверхностный слой находится как бы в натянутом состоянии, подобно упругой пленке. Эти пленки удерживают небольших насекомых – водомерок, маленькие металлические иголки и другие предметы. Поверхностное натяжение определяется природой жидкости. Для демонстрации действия поверхностного натяжения выпив чай, оставьте на дне чашки немного жидкости с чаинками. Чайной ложкой или спичкой осторожно коснитесь поверхности жидкости. Она тотчас «поползет» вверх, увлекая за собой чаинки. Это явление – результат действия поверхностного натяжения. Если две сухие стеклянные пластинки приложить друг к другу, они легко разъединяются. Если же одну из пластинок смочить водой, разъединить их будет значительно труднее. Это тоже результат действия поверхностного натяжения. Поверхностный слой оказывает давление на всю остальную массу жидкости. Это так называемое молекулярное давление, как оказалось, измеряется весьма внушительными цифрами. Для эфира, например, оно составляет 1400, для спирта 2400, а для воды 11000 атмосфер. В этом может заключаться одна из причин того, что капельные жидкости практически несжимаемы. Ведь обычное внешнее давление ничтожно по сравнению с тем, которое жидкость уже испытывает от своих же молекул – молекул поверхностного слоя. Вторая причина несжимаемости жидкости – малые расстояния между молекулами, половина из которых связана внутренними межмолекулярными связями. При создании новой поверхности жидкости требуется затрата энергии для преодоления сил внутреннего давления, которая характеризуется коэффициентом поверхностного натяжения s, измеряемым в Н/м. Коэффициент поверхностного натяжения рассматривается как сила, действующая на единицу длины поверхности раздела жидкости и соприкасающейся с ней среды, а также как работа, требуемая для образования единицы новой (межфазной) поверхности. С увеличением температуры жидкости поверхностное натяжение уменьшается, снижаясь до нуля в критической точке.
ЛАБОРАТОРНАЯ РАБОТА № 1
ИЗМЕРЕНИЕ ДАВЛЕНИЙ Задачи работы 1. Закрепление сведений о приборах для измерения давления. 2. Приобретение начальных навыков измерения медленно меняющегося давления и тарировки измерительных приборов. 3. Приобретение начальных навыков измерения быстропеременного давления и тарировки измерительного тракта. 4. Освоение методики статистической обработки результатов измерений с использованием ПЭВМ.
Быстропеременных давлений Схема лабораторной установки представлена на рис. 1.3. Она включает насосы (3) и (4), вентили питания водой (7) и (8), мембранный датчик давления (2), тензометрический усилитель (5), осциллограф (1) с гальванометром (6), образцовый манометр (9). В данной работе для измерения быстропеременных давлений используется измерительный комплекс, состоящий издатчика давления, тензометрического усилителя УТ-4, светолучевого осциллографа НО44. Мембранный датчик давления преобразует измеряемое давление в электрический сигнал малой величины, который увеличивается в тензометрическом усилителе. Сигнал с усилителя поступает в осциллограф со светочувствительной бумагой. В результате на светочувствительной бумаге изображается осциллограмма записи переменного давления в функции времени (рис. 1.4). На этой же осциллограмме записываются тарировочные уровни сигнала, позволяющие расшифровать запись.
Меняющихся давлений Схема лабораторной установки представлена на рис. 1.5. Она включает вентиль (1) питания водой от водопровода, сливной вентиль (9), вентиль жидкостного манометра (6) соединяющий жидкостной манометр (8) с измерительной шкалой (7), вентиль (5), соединяющий резервуар (3) с атмосферой, манометр (2) и мановакууметр (4). Литература 1. Байков, О.В. Лабораторный курс гидравлики и насосов / 2. Статистическая обработка экспериментальных данных: методические указания по выполнению лабораторной работы. – Орел: 3. Физический энциклопедический словарь / Под ред. А.М. Прохорова. – М.: Советская энциклопедия, 1983. – 928 с.
ЛАБОРАТОРНАЯ РАБОТА №2 Задачи работы 1. Закрепить сведения о видах гидравлических сопротивлений и способах их определения. 2. Измерить сопротивление трения движению жидкости по трубе. 3. Измерить местное сопротивление в трубе. 4. Проанализировать причины различий экспериментальных и расчетных данных.
Теоретические основы работы Существует два вида потерь гидравлического напора при движении жидкости: потери на трение при движении по прямым участкам трубопроводов и потери на вихреобразование при каждом изменении конфигурации проходного сечения. Первые из них называют потерями на трение (D Рт), а вторые - потерями на местных сопротивлениях (D Рм), т.е.
D Р = D Рт + D Рм . (2.1) Потери на местных сопротивлениях определяются формулой Вейсбаха, как часть динамического напора потока (н/м2) перед сопротивлением:
где r – плотность жидкости, кг/м3;
x – коэффициент местного сопротивления. Коэффициент местного сопротивления (x) зависит от критерия Рей-нольдса (Re) и от конфигурации проходного сечения в устройстве, являющимся местным сопротивлением:
где d – диаметр трубы (м) или другой характерный размер устройства; n – кинематическая вязкость жидкости, м2/c. Кинематическая вязкость жидкости зависит от температуры, и зависимость вязкости от температуры представлена на графике рис. 2.1. Зависимость коэффициента местного сопротивления от критерия Рейнольдса имеет место лишь при малых скоростях потока, соответствующих значениям критерия Рейнольдса Re <500. При практике местные сопротивления обычно работают при более высоких значениях критерия Рейнольдса. В этой области коэффициенты сопротивления остаются постоянными. Поэтому данная область (область Re > 500) называется областью автомодельности по критерию Re.
.
В ней местные сопротивления зависят только от конфигурации проходного сечения устройства, определяющего это сопротивление. Это позволяет составить справочные таблицы по гидравлическим сопротивлениям основных используемых в технике устройств. Потери гидравлического напора, связанные с распределенными по длине трубопровода потерями на трение, рассчитывают по формуле Дарси-Вейсбаха, так же как часть гидродинамического напора движущегося потока.
где l – коэффициент гидравлического сопротивления трения,
a – коэффициент Кориолиса. При Re < 2320 берется a»2. Коэффициент гидравлического сопротивления определяется двумя факторами – значением числа Рейнольдса и шероховатостью поверхности трубопровода. В связи с изменением характера течения при изменении критерия Рейнольдса изменяются также и зависимости для расчета коэффициентов гидравлического сопротивления. Каждая из расчетных зависимостей применима лишь в соответствующей области значения критерия Рейнольдса. На практике пользуются несколькими записями расчетных формул, наиболее распространенные из которых сведены в табл. 2.1. Используемые в расчетах величины шероховатости труб, изготовленных из различных материалов, представлены в табл. 2.2.
Анализ сопротивлений трения При работе установки вода насосом подается в исследуемый трубопровод (4), внутренний диаметр которого d 1=8 мм. Длина трубопровода равна 820 мм, это исключает возможность влияния различных местных особенностей (нарушение формы, размеров). Перед началом работы необходимо ознакомиться с данным методическим указанием и проверить исправность установки (рис. 2.2). 1.1 Открыть кран слива (7) и, открывая кран (1), установить максимальное значение расхода жидкости по показанию счетчика 1.2. Записать, в протокол испытаний реализованные значения расхода воды Q и высоту столба жидкости по манометрам h 1 и h 2. 1.3. Закрыть кран (1). 1.4. Выполнить действия по п.п. 1.1-1.3 последовательно для пяти значений расхода в области ламинарного течения и пяти значений расхода в области турбулентного течения. Показания манометров и счетчика воды записать в протокол испытаний соответственно для ламинарного и турбулентного режимов течения. 1.5. Вычислить экспериментальные значения коэффициента гидравлического сопротивления l э по экспериментальным данным для всех реализованных значений параметров (10 вычислений). Использовать для этого формулы:
6. Вычислить расчетные значения коэффициента гидравлического
7. Разделить область ламинарного и турбулентного режимов течения жидкости и отдельно для каждой из них найти среднее значение коэффициентов гидравлического сопротивления, определенных по экспериментальным и расчетным данным (l э, l р). Для этого использовать программу статистической обработки данных на ПЭВМ. 8. Вычислить по программе «statzna.raz» статистическую значимость различий экспериментальных и расчетных значений величин l э и l р для обеих областей течения жидкости. Занести все результаты оценок в табл. 2.3.
 
Вопросы для контроля 1. Чем различаются местные и распределенные по длине трубопровода сопротивления? 2. Какие виды течения жидкости различают? 3. Какие величины входят в критерий Рейнольдса и в чем заключается его физический смыл? 4. Каков физический смысл коэффициентов сопротивления?
Литература 1. Башта, Т.М. Гидравлика, гидромашины и гидроприводы: учебник для машиностроительных ВУЗов /Т.М. Башта, С.С. Руднев, 2. Идельчик, И.Б. Справочник по гидравлическим сопротивлениям / И.Б. Идельчик. – М.: Машиностроение, 1975. – 559 с. 3. Статистическая обработка экспериментальных данных: методические указания по выполнению лабораторной работы. – Орел:
Расходомер Вентури
В расходомере Вентури (рис. 3.4) искусственно создается перепад давления, измерив который можно рассчитать расход жидкости.
Рис. 3.4. Схема расходомера Вентури Для реального потока жидкости с достаточной для большинства технических измерений и исследований точностью в уравнении Бернулли (3.4) величины а 1 и а 2 можно принять равными единице. Для двух сечений горизонтального расходомера имеем:
На участке трубки 1–2 потери гидравлического напора можно принять равными нулю h п,1–2 = 0.
Тогда:
Величина Разность потенциальных энергий жидкости в сечениях I и II равна E 1 – E 2 = D h и измеряется с помощью пьезометров (рис. 3.4).
Следовательно:
(W 22 – W 12)/(2× g) = D h. (3.6)
В соответствии с законом сохранения массы имеем:
W 1 × S 1 = W 2 × S 2, (3.7) где S 1, S 2 – площади поперечных сечений I и II трубки Вентури С учетом (3.7) получим:
W 1 = W 2 × Подставив (3.6) в (3.4), найдем:
Расход жидкости равен Q:
где K т – постоянная расходомера Вентури:
K т =
Выражение для расхода жидкости можно получить и так:
где K т = Расходомерная диафрагма
Более простым по сравнению с предыдущим является метод измерения расхода жидкости с помощью измерительной шайбы или диафрагмы (рис. 3.5). Расход жидкости определяется по уравнениям (3.9 и 3.10).
Трубка Пито – Прандтля
Простейшим прибором для измерения скорости движущейся жидкости или газа является трубка Пито – Прандтля. Конструкция ее представлена на рис. 3.6. Она состоит из трубок прямой (1) и согнутой под прямым углом (2). Запишем уравнение Бернулли для сечений I и II.
где Р 1, Р 2 – гидростатические давления жидкости в сечениях I и II, g – ускорение свободного падения, м/с2.
В сечении II скорость жидкости или газа перед изогнутым концом трубки равна нулю W 2 = 0, т.к. здесь жидкость тормозится. Тогда из (3.11) получим:
где E 1, E 2 – потенциальные энергии жидкости в сечениях I и II. Поскольку E 2 – E 1 = D h, получим:
где D h – разность высот в пьезометрических трубках. Отсюда найдем скорость жидкости или газа W 1 в трубопроводе:
ЛАБОРАТОРНАЯ РАБОТА № 3
ИССЛЕДОВАНИЕ ПРЕОБРАЗОВАНИЯ ФОРМ ЭНЕРГИИ СТРУИ Цель работы: повышение уровня знаний о движении жидкости в трубопроводах, о преобразовании кинетической и потенциальной форм энергии в них.
Задачи работы 1. Убедиться на опыте в переходе кинетической энергии потока в потенциальную и обратно. 2. Оценить полноту преобразования форм энергии и связанные с этим гидравлические сопротивления. 3. Вычислить параметры преобразования форм энергии на отдельных участках экспериментального трубопровода и сравнивать результаты с экспериментальными данными. Теоретические основы работы Для реальной жидкости, уравнение Бернулли имеет вид
где r – плотность жидкости, кг/м3; V – скорость движения жидкости, м/с; Р – статическое давление, Па; h – нивелировочная высота жидкостной струи над уровнем её отсчета, м; g – ускорение силы тяжести, м/с2; D Р n – потери давления, на рассматриваемом участке, Па; a – коэффициент кинетической энергии (коэффициент Кариолиса), определяемый различиями средних по сечению местных скоростей течения жидкости. Уравнение Бернулли называют также основным уравнением гидродинамики, его физический смысл следующий: «Давление жидкости, текущей по трубе, больше там, где скорость движения жидкости меньше, и обратно: давление меньше там, где скорость движения жидкости больше» [3, с. 350-352]. Этот закон назван по имени швейцарского физика и математика Даниила Бернулли (1700-1782). Часто уравнение Бернулли записывают в несколько измененном виде
где
h – нивелировочная высота струи над нулевым уровнем отсчета; Н – полная гидравлическая высота (полное давление в жид- Это выражение читается так: «Полная гидравлическая высота столба жидкости, характеризующего его полное давление, складывается
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 193; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.015 с.) |

 Н.Н. Малахов
Н.Н. Малахов
 В.С. Ванин, Н.Н. Малахов, Т.В. Галаган,
В.С. Ванин, Н.Н. Малахов, Т.В. Галаган, В17 Ванин, В.С. Гидравлика: учебно-методическое пособие /
В17 Ванин, В.С. Гидравлика: учебно-методическое пособие / = r× g.
= r× g.
 ;
; о Е –
о Е – 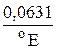 см2/с.
см2/с. (2.2)
(2.2) – скорость движения жидкости по трубопроводу перед местным сопротивлением, м/с;
– скорость движения жидкости по трубопроводу перед местным сопротивлением, м/с; (2.3)
(2.3)

 0,015
0,015
 0,010
0,010

 (2.4)
(2.4) , d – длина и диаметр трубопровода;
, d – длина и диаметр трубопровода; (2.5)
(2.5) (2.6)
(2.6) по формулам
по формулам при 2320< Re < 2×105 ; (2.7)
при 2320< Re < 2×105 ; (2.7) ; при Re < 2320; (2.8)
; при Re < 2320; (2.8)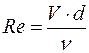 . (2.9)
. (2.9)


 . (3.5)
. (3.5)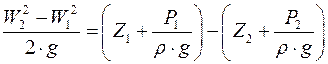 .
. = Е 1 представляет собой потенциальную энергию E 1 положения единичной массы жидкости и ее давления, аналогично
= Е 1 представляет собой потенциальную энергию E 1 положения единичной массы жидкости и ее давления, аналогично  = E 2.
= E 2. или W 2 = W 1 ×
или W 2 = W 1 ×  . (3.8)
. (3.8) .
. , (3.9)
, (3.9)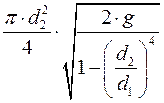 .
.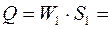
 , (3.10)
, (3.10) .
.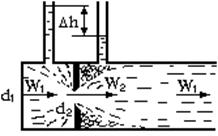 Рис. 3.5. Схема расходомерной диафрагмы
Рис. 3.5. Схема расходомерной диафрагмы
 , (3.11)
, (3.11) Рис. 3.6. Схема измерений, используемых в трубке
Пито – Прандтля
Рис. 3.6. Схема измерений, используемых в трубке
Пито – Прандтля
 ,
, , (3.12)
, (3.12) . (3.13)
. (3.13) ,
, ,
, – скоростная высота столба жидкости, являющаяся мерой скоростного напора струи жидкости, м;
– скоростная высота столба жидкости, являющаяся мерой скоростного напора струи жидкости, м; – пьезометрическая высота столба жидкости в струе, характеризующая статическое давление, м;
– пьезометрическая высота столба жидкости в струе, характеризующая статическое давление, м;


