
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Послідовність незалежних випробувань. Формули Бернуллі, Лапласа, ПуассонаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай проводиться серія з n незалежних випробувань, в кожному з яких ймовірність появи події А одна й та ж і рівна р (ймовірність непояви події А у випробуванні q = 1 – p). Тоді ймовірність Рn (m) того, що подія А з¢явиться у цих n випробуваннях m разів (0 ≤ m ≤ n) обчислюється за формулою Бернуллі
Ймовірність Рn (m 1, m 2) того, що в серії з n випробувань подія А відбудеться не менше m 1 і не більше m 2 разів (0 ≤ m 1 ≤ m 2 ≤ n) обчислюється за формулою Рn (m 1, m 2) = При великих значеннях n користуватись формулою Бернуллі для обчислення ймовірності Рn (m) досить складно, оскільки потрібно виконувати великий об’єм обчислень. Якщо число випробувань n велике, а ймовірність р не мала (np ≥ 9), для обчислення ймовірності Рn (m) користуються наближеною (тим точнішою, чим більше число n) локальною формулою Лапласа
де
В цих же випадках для обчислення ймовірності Рn (m 1 , m 2) використовують інтегральну формулу Лапласа Pn (m 1, m 2) ≈ Ф(х 2) – Ф(х 1), (4.4)
де
Значення функцій φ(х) (функція Гаусса) та Ф(х) (функція Лапласа) знаходять за таблицями (див. Додатки 1,2), враховуючи при цьому парність функції φ(х) та непарність функції Ф(х). Крім того, вважається, що при х ³ 4 φ(х)=0, а при х ³ 5 Ф(х)=0,5. У випадку, коли число випробувань n велике, а ймовірність р мала (nр < 9), застосування формул Лапласа (4.3) – (4.4) приводить до значних похибок. В таких випадках для обчислення ймовірності Рn (m) застосовують асимптотичну формулу Пуассона
де l = np ‑ параметр формули Пуассона. Ймовірність Рn (m 1 , m 2), як і раніше, обчислюють за формулою (4.2). Формула Пуассона (4.5) використовується також і для підрахунку ймовірності появи різного числа подій (наприклад, точок або інших елементів) в якій-небудь області (плоскій, просторовій, за певний проміжок часу і т.і.). При розв’язанні задач з використанням формули Пуассона початкові дані можуть зустрічатись у двох варіантах: 1) в умові задачі вказується ймовірність р появи події в одному випробуванні і число випробувань n; 2) в умові задачі вказується середнє число l1 появ події в якій-небудь одиниці області (площі, об’єму, часу і т.і.) і розмір s області (площі, об’єму, часу), всередині якої з’являються події, що нас цікавлять.
У першому випадку параметр формули Пуассона знаходиться за формулою l = np. У другому випадку цей параметр обчислюють за формулою l = l1· s. Подальші розрахунки ймовірності за формулою Пуассона проводяться однаково для обох випадків. Ймовірність того, що відхилення відносної частоти
Найбільш імовірне число m 0 появ події А в n незалежних випробуваннях визначається з подвійної нерівності np – q ≤ m 0 ≤ np + p. (4.7) Кількість дослідів N, які потрібно провести, щоб з імовірністю P можна було стверджувати, що подія А відбудеться хоч один раз, знаходять з умови
Опитування з теорії 1. Яка послідовність випробувань називається послідовністю незалежних випробувань (схемою Бернуллі)? 2. Сформулювати дві основні задачі, пов¢язані зі схемою Бернуллі. 3. Записати формулу Бернуллі. 4. Сформулювати локальну теорему Лапласа і вказати умови її застосування. 5. Сформулювати інтегральну теорему Лапласа і вказати умови її застосування. 6. Сформулювати граничну теорему Пуассона і вказати умови її застосування. 7. Як знайти найбільш імовірне числопояв події в n незалежних випробуваннях? 8. Як знайти кількість дослідів N, які потрібно провести, щоб з імовірністю P можна було стверджувати, що дана подія відбудеться хоч один раз?
Задача 1. Прилад складається з 5-ти елементів. Елементи однаково надійні, працюють і виходять з ладу незалежно один від одного. Ймовірність відмови елемента за час Т дорівнює 0,2. Знайти ймовірність того, що за час Т: а) відмовить один елемент; б)відмовить хоч один елемент; в) відмовить не більше двох елементів. Розв”язання. Нехай подія А = ²відмова елемента за час Т². Тоді p = P (A)=0,2, q =1- p= 0,8. Ймовірність p = P (A) події А однакова для всіх п”яти елементів, вихід з ладу кожного з них не залежить від того, працюють чи ні інші елементи. Тому можна застосувати формулу Бернуллі. а) Маємо n = 5, m = 1. За формулою Бернуллі
б) Подія В = ²за час Т відмовить хоч один елемент ² відбувається тоді, коли за цей час відмовить або один, або два, …, або всі 5 елементів. Отже, потрібно знайти ймовірність Pn (m 1, m 2) при n = 5, m 1 = 1, m 2 = 5, тобто ймовірність Р (В) = P5 (1; 5).
Замість того, щоб застосовувати формулу (4.2), врахуємо наступне. Протилежною для події В буде подія Р (В) = 1 – Р ( в) Подія С = ²за час Т відмовить не більше двох елементів ² відбувається тоді, коли за цей часвідмовить або один, або два елементи, або не відмовить жоден з п¢яти елементів. Отже, Р (С) = P5 (0; 2) = Р 5 (0) + Р 5 (1) + Р 5 (2). Оскільки Р 5 (2) = то, враховуючи п.п. а), б), маємо Р (С) = 0,33 + 0,41 + 0,2 =0,94.
Задача 2. Приживається 90% саджанців чорної смородини. Скільки потрібно посадити саджанців, щоб з імовірністю не меншою 0,95 хоч один саджанець прижився? Розв”язання. Нехай подія А = “саджанець прижився”. Тоді p = Р (А)=0,9, q =1- p= 0,1. Якщо висаджено n саджанців, то ймовірність того, що хоч один з них приживеться, дорівнює Рn (1; n). Отже, потрібно знайти n з умови Рn (1; n) ³ 0,95. Але Рn (1; n) = 1 - Рn (0), тому слід розв”язати нерівність 1 - Рn (0) ³ 0,95, тобто нерівність Рn (0) £ 0,05. (4.9) Якщо взяти n = 1, то Рn (0) = Р 1(0) = Отже, якщо висадити два саджанці чорної смородини, то з імовірністю не меншою 0,95 хоч один з них приживеться. Зауваження. Той же результат дістанемо, застосувавши формулу (4.8) при Р = 0,95, р = 0,9:
тобто N ³ 2. Задача 3. Схожість насіння даного сорту пшениці дорівнює 0,9. Знайти ймовірність того, що з 900 висіяних зерен проросте: а) 800 зерен; б) від 790 до 830 зерен; в) не менше 800 зерен. Розв”язання. Під дослідом у цій задачі маємо на увазі висівання зернини, подія А = “зерно проросло”. Тоді р = Р (А) = 0,9, q = 1- р = 0,1. Висівається 900 зерен, тому n = 900. Оскільки число дослідів n велике, ймовірність р події А теж велика (np = 810), для обчислення потрібних імовірностей застосовуємо формули Лапласа (4.3), (4.4). а) Маємо n = 900, m = 800. Для обчислень за формулою (4.3) знаходимо
Отже,
(врахували парність функції Гаусса j(х) і її значення φ(1,11) = 0,2155 з таблиці Додатку 1). б) Маємо n = 900, m 1 = 790, m 2 = 830. Для обчислень за формулою (4.4) знаходимо
Отже, Р 900(790;830) ≈ Ф(2,22) – Ф(– 2,22) = Ф(2,22) + Ф(2,22) = 2 Ф(2,22)= = 2×0,4868 = 0,9736 (врахували непарність функції Лапласа Ф(х) та її значення Ф(2,22) = 0,4868 з таблиці Додатку 2). в) Вимога, щоб проросло не менше 800 зерен пшениці, означає, що має прорости або 800, або 801, …, або всі 900 висіяних зерен. Отже, маємо n = 900, m 1 = 800, m 2 = 900. Як і в п. б) обчислюємо
Шукана ймовірність Р 900(800;900) ≈ Ф(10) – Ф(– 1,11) = Ф(10) + Ф(1,11) = 0,5 + 0,3665= = 0,8665. Задача 4. Ремонтна база обслуговує 8 господарств, з кожного з яких може поступити заявка на черговий день з імовірністю 0,3 незалежно від заявок інших господарств. Знайти найбільш імовірне число заявок, які поступають за день, і ймовірність отримання такого числа заявок. Розв”язання. Нехай А = “надходження заявки на черговий день”. За умовою задачі n = 8, p = P (A)=0,3, q =1- p= 0,7. Найбільш імовірне число m 0 заявок, які надійдуть з господарств за день, обчислюємо з умови (4.7) np – q ≤ m 0 ≤ np + p. Маємо np – q = 8×0,3 – 0,7 = 2,4 – 0,7 = 1,7; np + p =2,4 + 0,3 =2,7. Отже, 1,7 ≤ m 0 ≤ 2,7, звідки m 0 = 2. Ймовірність того, що на черговий день з господарств надійде дві заявки, знаходимо за формулою Бернуллі Р 8 (2) = Задача 5. Станок-автомат відштампував 400 деталей. Ймовірність того, що виготовлена деталь виявиться бракованою, дорівнює 0,2. Знайти з імовірністю 0,9544 межі, в яких буде лежати число m стандартних деталей серед 400 виготовлених.
Розв”язання. Нехай подія А = “деталь стандартна”. Скористаємося формулою (4.6), ліву частину якої можна подати у вигляді
Отже, Р (n (p – ε) ≤ m ≤ n (p+ ε)) За умовою задачі n = 400, p = P (A)=0,8, q =1– p= 0,2 і
За таблицею (Додаток 2) знаходимо Ф(2) = 0,4772, тому 50e = 2 і e=0,04. Таким чином, число m стандартних деталей серед 400 виготовлених з імовірністю 0,9544 лежить в межах 400 (0,8 – 0,04) ≤ m ≤ 400 (0,8 + 0,04), або 304 ≤ m ≤ 336. Задача 6. В одному з корпусів університету використовується 500 електричних ламп. Ймовірність перегорання однієї лампи протягом місяця дорівнює 0,004. Знайти ймовірність того, що протягом місяця перегорить: а) рівно дві електричних лампи; б) хоч одна лампа; в) не більше двох електричних ламп. Розв”язання. За умовою задачі n = 500 - велике, p =0,004 - мале, l = np = 2. Для підрахунку вказаних імовірностей застосовуємо формулу Пуассона (4.5): а) б) Р 500 (1;500) = 1- Р 500 (0) в) Р 500 (0;2) = Р 500 (0) + Р 500 (1) + Р 500 (2)» 0,1353 + = 0,1353 + 0,2706 + 0,2706 = 0,6765. Задача 7. Середнє число викликів, які надходять на АТС за одну хвилину, дорівнює 3. Знайти ймовірність того, що за 2 хвилини надійде: а) 4 виклики; б) не більше чотирьох викликів; в) не менше чотирьох викликів. Розв”язання. Для обчислення потрібних імовірностей використаємо формулу Пуассона. За умовою задачі l1 = 3 а) р 4 б) Р = р 0 + р 1 + р 2 + р 3 + р 4 + в) Р = 1 – (р 0 + р 1 + р 2 + р 3) = 1- (e -6 + 6 e -6 +18 e -6 +36 e -6) = = 1 - 61 e -6 = 1 - 61×0,00248 = 1- 0,15128» 0,849.
Задачі для аудиторної і самостійної роботи
1. Продукція деякого виробництва містить 5% браку. Знайти ймовірність того, що серед п’яти взятих навмання виробів: а) не буде жодного бракованого; б) буде два бракованих. Відповідь: a) 0,77; б) 0,02. 2. Два рівносильні суперники грають в шахи. Що більш імовірно: а) виграти одну партію з двох чи дві партії з чотирьох? б) виграти не менше двох партій з чотирьох чи не менше трьох партій з п’яти? Нічиї до уваги не беруться. Відповідь: a) P 2(1) = 1/2, P 4(2) = 3/8 i P 2(1) > P 4(2); б) P 4(2,4) = 11/16, P 5(3,5) = 1/2 i P 4(2,4) > P 5(3,5). 3. Приживається 80% саджанців даного сорту яблуні. Скільки потрібно посадити саджанців, щоб з імовірністю не менше 0,95 хоч один саджанець прижився? Відповідь: 2.
4. Ймовірність влучення в мішень при одному пострілі дорівнює 0,8. Знайти ймовірність того, що при 100 пострілах буде: а) 75 влучень; б) не менше 75 влучень; в) від 75 до 90 влучень. Відповідь: a) 0,04565; б) 0,8944; в) 0,8882. 5. Станок-автомат штампує деталі. Ймовірність того, що виготовлена деталь виявиться бракованою, дорівнює 0,2. Знайти ймовірність того, що серед 400 деталей буде: а) 62 браковані деталі; б) не більше 70 бракованих деталей; в) не менше 80 бракованих деталей. Відповідь: a) 0,004; б) 0,1056; в) 0,5. 6. ВТК перевіряє партію з десяти деталей. Ймовірність того, що деталь стандартна, дорівнює 0,75. Знайти найбільш імовірне число деталей, які будуть визнані стандартними. Відповідь: 8. 7. Стрілець робить 14 пострілів в мішень. Ймовірність влучення при одному пострілі дорівнює 0,2. Знайти найбільш імовірне число влучень і ймовірність цього числа влучень. Відповідь: 2 i 3; 0,25. 8. Відділ технічного контролю перевіряє на стандартність 900 деталей. Ймовірність того, що деталь стандартна, дорівнює 0,9. Знайти з імовірністю 0,9544 межі, в яких буде лежати число m стандартних деталей серед перевірених. Відповідь: 792 Ј m Ј 828. 9. Гральний кубик підкидають 80 разів. Знайти з імовірністю 0,9973 межі, в яких буде лежати число m появ шести очок. Відповідь: 3 Ј m Ј 23. 10. Завод відправив на базу 500 виробів. Ймовірність пошкодження виробу при транспортуванні дорівнює 0,002. Знайти ймовірність того, що в дорозі буде пошкоджено: а) рівно три вироби; б) менше трьох виробів; в) більше трьох виробів; г) хоч один виріб. Відповідь: a) 0,0613; б) 0,9197; в) 0,019; г) 0,632. 11. Апаратура містить 2000 однаково надійних елементів, ймовірність відмови для кожного з яких дорівнює 0,0005. Знайти ймовірність відмови апаратури, якщо вона відбувається при відмові хоч одного з елементів. Відповідь: 0,632. 12. Насіння містить 0,1% зерен бур’янів. Знайти ймовірність того, що серед 2000 випадково відібраних зерен буде 5 насінин бур’янів. Відповідь: 0,036. 13. В середньому на 1 м2 посівів зустрічається одна бур’янина. Знайти ймовірність того, що на площі 3 м2 виявиться більше двох стебел бур’яну. Відповідь: 0,5767.
Практичне заняття 5
|
||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.156.84 (0.008 с.) |

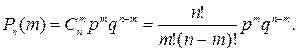 (4.1)
(4.1) . (4.2)
. (4.2)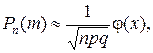 (4.3)
(4.3)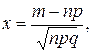

 ,
,  ,
, 
 , (4.5)
, (4.5) появи події А в n незалежних випробуваннях від імовірності р = Р (А) появи цієї події в одному випробуванні за абсолютною величиною не перевищить заданого числа ε > 0, обчислюється за формулою
появи події А в n незалежних випробуваннях від імовірності р = Р (А) появи цієї події в одному випробуванні за абсолютною величиною не перевищить заданого числа ε > 0, обчислюється за формулою . (4.6)
. (4.6) (4.8)
(4.8)
 ²за час Т не відмовить жоден з п¢яти елементів ². Тому
²за час Т не відмовить жоден з п¢яти елементів ². Тому ) = 1 – Р 5 (0) = 1 -
) = 1 – Р 5 (0) = 1 -  = 1– 0,85 » 1– 0,33=0,67.
= 1– 0,85 » 1– 0,33=0,67. 10×0,02048» 0,2,
10×0,02048» 0,2, =0,1 > 0,05 і нерівність (4.9) не виконується. При n =2 Рn (0) = Р 2(0) ==
=0,1 > 0,05 і нерівність (4.9) не виконується. При n =2 Рn (0) = Р 2(0) ==  = 0,01 < 0,05, тобто нерівність (4.9) виконується.
= 0,01 < 0,05, тобто нерівність (4.9) виконується. =
=  ,
,
 ≈
≈ 





 28×0,09×0,1176» 0,2965.
28×0,09×0,1176» 0,2965. = Р (– ε ≤
= Р (– ε ≤  ≤ ε) = Р (n (p – ε) ≤ m ≤ n (p+ ε)).
≤ ε) = Р (n (p – ε) ≤ m ≤ n (p+ ε)). .
. або Ф(50e) = 0,4772.
або Ф(50e) = 0,4772.

 +0,2706 =
+0,2706 = , s = 2 хв, отже параметр формули Пуассона дорівнює l = l1× s =3×2 = 6. Позначимо через р k ймовірність надходження k викликів за дві хвилини. Тепер маємо:
, s = 2 хв, отже параметр формули Пуассона дорівнює l = l1× s =3×2 = 6. Позначимо через р k ймовірність надходження k викликів за дві хвилини. Тепер маємо: 54×0,00248»0,134;
54×0,00248»0,134; +
+  +
+  +
+ +
+  = e -6 + 6 e -6 +18 e -6 +36 e -6 +54 e -6 =115×0,00248=0,285;
= e -6 + 6 e -6 +18 e -6 +36 e -6 +54 e -6 =115×0,00248=0,285;


