
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неперервні випадкові величиниСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Серед випадкових величин виділяють дискретні (див. заняття 5) та неперервні випадкові величини. Неперервна випадкова величина відрізняється від дискретної тим, що вона приймає всі значенняз деякого проміжку (скінченного чи нескінченного). Але не всяка така випадкова величина називається неперервною. Випадкова величина називається неперервною, якщо її функцію розподілу можна представити у вигляді Якщо Функція розподілу 1) неперервна зліва; 2) неспадна на 3) Кожна функція, яка має властивості 1), 2), 3), є функцією розподілу деякої випадкової величини.
Властивості щільності розподілу ймовірностей 1. 3. Зауваження. Якщо всі можливі значення випадкової величини належать проміжку Основі числові характеристики неперервної випадкової величини Математичне сподівання М (Х), дисперсія D (X)і середнє квадратичне відхилення s(Х) неперервної випадкової величини Х, заданої щільністю розподілу
(при умові, що цей інтеграл абсолютно збіжний),
Якщо всі можливі значення випадкової величини Х належать відрізку
Основні закони розподілу неперервних випадкових величин 1. Рівномірний розподіл. Випадкова величина розподілена рівномірно на проміжку 2. Показниковий розподіл. Випадкова величина розподілена за показниковим законом з параметром 3. Нормальний розподіл. Випадкову величину називають нормально розподіленою з параметрами а і Графік цієї функції називають кривою Гаусса. Дві випадкові величини називаються незалежними, якщо закон розподілу однієї з них не залежить від того, які можливі значення прийняла друга величина. Інакше величини називаються залежними . Кілька випадкових величин називаються взаємнонезалежними, якщо закони розподілу будь-якого числа з них не залежать від того, які можливі значення прийняли інші величини.
Опитування з теорії 1. Дати означення неперервної випадкової величини. 2. Дати означення функції розподілу неперервної випадкової величини і навести її основні властивості. 3. Що таке щільність розподілу неперервної випадкової величини і які її властивості. 4. Навести основні розподіли неперервної випадкової величини. 5. Які основні числові характеристики неперервної випадкової величини, як вони обчислюються?
Задача 1. Випадкова величина Х задана функцією розподілу Знайти: 1) щільність розподілу Розв’язання. 1)Для знаходження щільності розподілу використаємо формулу 2) Знайдемо ймовірність попадання Х в інтервал 3)
Задача 2. Випадкова величина Х задана функцією розподілу Знайти параметр Розв’язання. Знаходимо щільність розподілу Враховуючи вигляд та властивості щільності розподілу, дістанемо
Задача 3. Задана щільність розподілу неперервної випадкової величини Розв’язання. Визначимо параметр а, використовуючи властивість 2 щільності розподілу:
Задача 4. Випадкова величина Х має щільність розподілу Розв’язання. За властивістю 3 щільності розподілу Задача 5. Нехай Розв’язання. Позначимо шукану функцію розподілу
Аналогічно позначимо шукану щільність розподілу
Тут ми використали, що Задача 6. Неперервна випадкова величина Х має функцію розподілу Розв’язання. Позначимо шукану функцію розподілу
Задача 7. Щільність розподілу неперервної випадкової величини Х є Розв’язання. Позначимо шукану щільність розподілу Задача 8. Які з поданих нижче функцій є функціями розподілу: а) Розв’язання. а)Перевіряємо, чи виконуються основні властивості функції розподілу 1 – 3. б) Зауважимо, що ця функція є неперервною у всій області визначення, тому вл.1 виконується. Покажемо, що вона неспадна (вл.2):
Властивість 3) виконується, оскільки
Задача 9. Щільність розподілу випадкової величини Х дорівнює а) коефіцієнт а; б) функцію розподілу; в) Розв’язання. а) Знайдемо параметр а: б) Знайдемо функцію розподілу: при
при в) Задача 10. Неперервна випадкова величина Знайти функцію розподілу Розв’язання За означенням
Таким чином,
Графіки
Щільність розподілу f(x)
Функція розподілу F(x) Задача 11. Випадкова величина Х рівномірно розподілена на відрізку Розв’язання. Позначимо через
Задача 12. Радіус круга – рівномірно розподілена величина Х на відрізку Розв’язання. Позначимо площу круга
Задачі для аудиторної та самостійної роботи 1. Випадкова величина Х задана щільністю розподілу Відповідь: 2. Випадкова величина Х задана щільністю розподілу
3. При яких значеннях параметрів функція буде функцією розподілу неперервної випадкової величини? Відповідь: 4. В умовах попередньої задачі знайти щільність розподілу, 5. Випадкова величина Відповідь: 6. В умовах попередньої задачі знайти щільність розподілу випадкової величини Відповідь: Відповідь: 9. Показати, що функція Відповідь: 10. Для рівномірно розподіленої величини Відповідь: 11 В умовах попередньої задачі знайти щільність розподілу Відповідь: 12. Показати, що функція
Практичне заняття 7
|
||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1073; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.96 (0.009 с.) |

 , де
, де  –деяка функція, яку називають щільністю розподілу ймовірностей (диференціальною функцією розподілу).
–деяка функція, яку називають щільністю розподілу ймовірностей (диференціальною функцією розподілу). диференційовна і похідна її обмежена, то Х неперервна і має щільність розподілу ймовірностей
диференційовна і похідна її обмежена, то Х неперервна і має щільність розподілу ймовірностей  . Графік функції
. Графік функції  ;
; .
. для всіх
для всіх  . 2.
. 2. 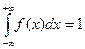 .
.
 .
. , то
, то  .
.
 ,
, .
. , то мають місце формули
, то мають місце формули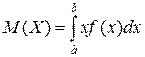 ;
; 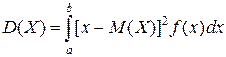 =
= 
 .
. , якщо щільність розподілу її має вигляд
, якщо щільність розподілу її має вигляд 
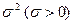 , якщо щільність її розподілу має вигляд
, якщо щільність її розподілу має вигляд  .
. .
. 2) ймовірність попадання Х в інтервал
2) ймовірність попадання Х в інтервал  ; 3)
; 3)  .
.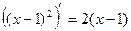 , то
, то 
 .
.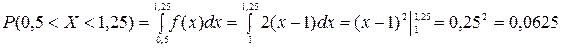
 ;
;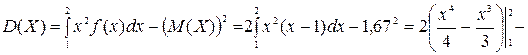
 ;
; 
 .
. щільність розподілу
щільність розподілу  .
.
 .
. . Отже, а =1,
. Отже, а =1, ,
,  .
. . Знайти параметр а, функцію розподілу
. Знайти параметр а, функцію розподілу  ,
, 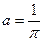 . Тепер
. Тепер 
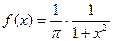 . Обчислити ймовірність
. Обчислити ймовірність  .
.
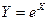 .
.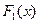

 .
. .
. .
. =
= 
 .
. . Знайти щільність розподілу випадкової величини
. Знайти щільність розподілу випадкової величини  .
. . Маємо
. Маємо  , де
, де  .Знайдемо
.Знайдемо 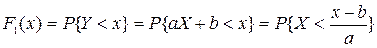 . Тепер
. Тепер 
 ; б)
; б) 
 . Знайдемо границю
. Знайдемо границю  , тобто вл.3 не виконується.
, тобто вл.3 не виконується. при
при  .
. Отже, дана функція є функцією розподілу.
Отже, дана функція є функцією розподілу.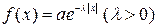 . Обчислити:
. Обчислити: .
.
 ,
, 



 маємо
маємо  .
. оскільки функція xf (x) непарна і інтеграл береться по симетричному відносно початку координат проміжку.
оскільки функція xf (x) непарна і інтеграл береться по симетричному відносно початку координат проміжку. задана щільністю розподілу
задана щільністю розподілу  .
. .
.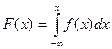 . Якщо
. Якщо  . При
. При  маємо
маємо 


 . При
. При  маємо
маємо 
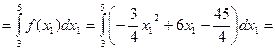
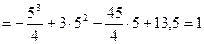 .
. .
.
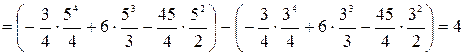 ;
;
 ;
; .
.

 . Знайти щільність розподілу випадкової величини
. Знайти щільність розподілу випадкової величини  ,
, 
 відповідно щільність розподілу і функцію розподілу
відповідно щільність розподілу і функцію розподілу  і
і  .
. 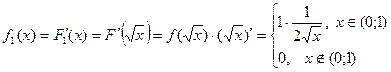 .
. ;
; 
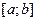 . Знайти щільність і функцію розподілу площі круга.
. Знайти щільність і функцію розподілу площі круга.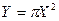 ,її функцію розподілу і щільність розподілу відповідно
,її функцію розподілу і щільність розподілу відповідно 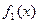 . Тоді
. Тоді  при
при  при
при  .
.  .
. . Звідки
. Звідки  . Знайдемо функцію розподілу:
. Знайдемо функцію розподілу: 
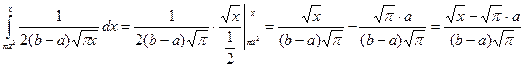 ,
,  . Остаточно
. Остаточно  .
. . Знайти: 1) функцію розподілу
. Знайти: 1) функцію розподілу  2) ймовірність попадання Х в інтервал
2) ймовірність попадання Х в інтервал 
 ;
;  .
. , де
, де  . Знайти: 1) функцію розподілу
. Знайти: 1) функцію розподілу  ; 3)
; 3)  . Відповідь:
. Відповідь: 
 ;
;  .
.
 .
. .
. .
.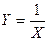 . Відповідь:
. Відповідь:  .
.  . Знайти щільність розподілу площі круга
. Знайти щільність розподілу площі круга  і обчислити ймовірність
і обчислити ймовірність  .
. ;
;  і 0 в інших випадках.
і 0 в інших випадках.  .
. .
. є щільністю розподілу випадкової величини. Знайти
є щільністю розподілу випадкової величини. Знайти  .
.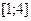 знайти функцію розподілу випадкової величини
знайти функцію розподілу випадкової величини  .
. .
.
 .
. є функцією розподілу неперервної випадкової величини. Знайти відповідну щільність розподілу. Відповідь:
є функцією розподілу неперервної випадкової величини. Знайти відповідну щільність розподілу. Відповідь:  .
.


