
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие и виды абсолютных величинСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Изучая массовые общественные явления, статистика в своих выводах опирается на числовые данные, полученные в конкретных условиях места и времени. Результаты статистического наблюдения регистрируются прежде всего в форме первичных абсолютных величин. Так, основная масса народнохозяйственных абсолютных показателей фиксируется в первичных учетных документах. Абсолютная величина отражает уровень развития явления. В статистике все абсолютные величины являются именованными, измеряются в конкретных единицах и, в отличие от математического понятия абсолютной величины, могут быть как положительными, так и отрицательными (убытки, убыль, потери и т.п.). Натуральные единицы измерения могут быть простыми (тонны, штуки, метры, литры) и сложными, являющимися комбинацией нескольких разноименных величин (грузооборот железнодорожного транспорта выражается в тонно-километрах, производство электроэнергии – в киловатт-часах). В статистике применяют и абсолютные показатели, выраженные в условно-натуральных единицах измерения (например, различные виды топлива пересчитываются в условное топливо). Стоимостные единицы измерения используются, например, для выражения объема разнородной продукции в стоимостной (денежной) форме – рублях. При использовании стоимостных измерителей принимают во внимание изменения цен с течением времени. Этот недостаток стоимостных измерителей преодолевают применением "неизменных" или "сопоставимых" цен одного и того же периода. В трудовых единицах измерения (человеко-днях, человеко-часах) учитываются общие затраты труда на предприятии, трудоемкость отдельных операций. С точки зрения конкретного исследования совокупность абсолютных величин можно рассматривать как состоящую из показателей индивидуальных, характеризующих размер признака у отдельных единиц совокупности, и суммарных, характеризующих итоговое значение признака по определенной части совокупности. Поскольку абсолютные показатели – это основа всех форм учета и приемов количественного анализа, то следует разграничивать моментные и интервальные абсолютные величины. Первые показывают фактическое наличие или уровень явления на определенный момент, дату (например, наличие запасов материалов или оборотных средств, величина незавершенного производства, численность проживающих и т.д.). Вторые – итоговый накопленный результат за период в целом (объем произведенной продукции за месяц или год, прирост населения за определенный период, величина валового сбора зерна за год и за пятилетку и т.п.).
Относительные величины Относительные величины являются обобщающими показателями, полученными в результате деления двух величин. Относительные величины подразделяются на следующие виды: · Относительная величина планового задания, рассчитываемая как отношение планового задания данного (текущего) периода к фактическому уровню предыдущего периода (расчет проводят в процентах). · Относительная величина выполнения плана – отношение фактического уровня данного (текущего) периода к фактическому уровню одного из предыдущих периодов (рассчитывается в процентах). · Относительная величина динамики – отношение фактического уровня данного (текущего) периода к фактическому уровню одного из предыдущих периодов (рассчитывается в коэффициентах или процентах). Произведение относительных величин выполнения плана и планового задания равно относительной величине динамики. · Относительная величина структуры, получаемая как отношение частей совокупности к объему всей совокупности (рассчитывается в процентах). · Относительная величина сравнения – отношение одноименных показателей, взятых за один и тот же период или момент времени, но характеризующих разные территории или объекты. · Относительная величина координации – отношение частей совокупности друг к другу. · Относительная величина интенсивности – соотношение разноименных абсолютных величин, связанных между собой, характеризующее степень распространения явления в определенной среде. Тема 5. СРЕДНИЕ ВЕЛИЧИНЫ Понятие о средней величине Структурные средние Понятие о средней величине Средняя величина является обобщающей количественной характеристикой изучаемого признака в исследуемой совокупности. В статистке используются разного рода средние величины. Средняя арифметическая – частное от деления суммы вариант на их число. Она бывает следующих видов: простая и взвешенная. Средняя арифметическая простая, рассматривается в случае, когда известны все значения признаков х₁,х₂..,хn и рассчитывается по формуле:
x = (x₁ + x₂ + … + xn) /n =∑x / n где n – число вариант; х – значение признака. Средняя арифметическая взвешенная, исчисляется, если известны отдельные значения признаков и их частоты, по следующей формуле:
х =∑xf / ∑f, где х- значение признака; f – частота, которая может быть абсолютной (в разах) и относительной (доля, удельный вес частот во всей совокупности) величиной.
Средняя арифметическая имеет следующие свойства: · Произведение средней арифметической на сумму частот равно сумме произведений вариант на соответствующие им частоты; · Если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число; · Если все варианты уменьшить или увеличить на одно и то же число раз, то средняя арифметическая из этих вариант уменьшится или увеличится во столько же раз; · Если все частоты одинаково уменьшить или увеличить в одно и то же число раз, то средняя арифметическая не изменится; · Сумма отклонений вариант от их средней арифметической величины равна нулю. Средняя гармоническая – это величина, обратная средней арифметической из обратных значений признака. Данный показатель применяется тогда, когда неизвестна численность совокупности и приходится взвешивать варианты по объемам признака. Средняя гармоническая также может быть простой и взвешенной. Средняя гармоническая простая исчисляется по формуле:
x = n /
Средняя гармоническая взвешенная исчисляется по формуле: х = ∑W / где W = xf - вес средней гармонической.
Средняя квадратическая – (и т.д. для любой степени) рассчитывается по следующим формулам Простая: х = корень из Взвешенная: х = корень из
Структурные средние В качестве структурных средних чаще всего используются показатели моды и медианы. Мода (Мо) – наиболее часто повторяющееся значение признака. Медиана (Ме) – величина признака, коотрая делит упорядоченный ряд на две равные по численности части. Если расчет моды и медианы проводится в дискретном ряду, то он опирается на их понятие. В интервальном ряду распределения для расчета моды и медианы применяются следующие формулы. Мода рассчитывается по формуле:
Мо = Хмо + Iмо ⋅(fMo – fMo -1) / ((fMo – fMo -1) + (fMo – fMo +1))
Где Хмо – нижнее значение модального интервала; Iмо – размер модального интервала; fMo – частота модального интервала; fMo -1 - частота, предшествующая модальной частоте; fMo +1 - частота, последующая за модальной частотой.
Модальному интервалу соответствует наибольшая (модальная) частота. Медиана рассчитывается по формуле:
Ме = Хме + IMe ⋅ (∑f / 2 – SMe-1) / fMe Где Хме –нижнее значение медианного интервала; IMe - размер медианного интервала; SMe-1- сумма частот, предшествующих медианной частоте; Медианному интервалу соответствует медианная частота. Таким интервалом будет интервал, сумма накопленных частот которого равна или превышает половину суммы всех частот.
Тема 6. ПОКАЗАТЕЛИ ВАРИАЦИИ
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 761; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.007 с.) |


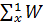
 / n
/ n



