
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Види відносних величин і способи їх обчисленняСодержание книги
Поиск на нашем сайте
За своєю суттю і пізнавальним значенням відносні величини поділяються на такі види: відносні величини виконання договірних зобов'язань, динаміки, структури, координації, порівняння у просторі, інтенсивності. Щодо відносної величини виконання плану, то вона в зв'язку з переходом економіки України на ринкові умови розраховуватися не буде. Замість неї розраховується відносна величина виконання договірних зобов'язань - показник, що визначається шляхом ділення обсягу фактично виконаних зобов'язань (наприклад, обсяг фактично поставленої продукції) на обсяг зобов'язань, передбачених договором (обсяг поставки продукції згідно договору). Розрахований таким способом показник характеризує ступінь виконання підприємством своїх договірних зобов'язань. Відносними величинами динаміки називаються показники, які виражають ступінь зміни явищ в часі Вони характеризують напрям і швидкість зміни явищ в часі, темпи їх розвитку. Відносні величини динаміки мають велике значення та широке застосування у статистиці і соціально-економічних дослідженнях. Це зумовлено тим, що вивчення розвитку явищ в часі, зокрема, розвитку народного господарства держави - важливе теоретичне і практичне завдання. Відносну величину динаміки визначають відношенням рівня (значення) показника за звітний період (рік, квартал, місяць і т.д.) до його рівня за минулий період. Для того, щоб розрахувати відносну величину динаміки, необхідно мати дані щонайменше за два періоди або моменти часу. Для того, щоб охарактеризувати інтенсивність зміни виробництва електроенергії атомними електростанціями України за період 1985-1995 pp., можна відносну величину динаміки обчислювати двояко. Зокрема, можна виробництво електроенергії у кожному наступному році, починаючи з 1992 року, співвідносити з виробництвом електроенергії у кожному попередньому році. Але ж можна виробництво кожного року зіставляти з виробництвом одного будь-якого року, взятого за базу порівняння, наприклад, з виробництвом у 1985р. Отже при обчисленні відносних величин динаміки постає питання про вибір бази(основи) порівняння. Залежно від характеру бази порівняння розрізняють два види відносних величин динаміки: відносні величини динаміки з змінною базою порівняння (ланцюгові) і відносні величини динаміки з постійною базою порівняння (базисні). Якщо відносні величини динаміки з змінною базою порівняння характеризують швидкість зміни величини показника від одного періоду до іншого, то базисні відносні величини характеризують поступове віддалення цього ж показника від періоду, який взято за базу порівняння. Питання про вибір бази порівняння для базисних відносних величин, має істотне значення. За базу порівняння слід брати дані за роки, які мають особливо важливе значення для розвитку досліджуваного процесу. Відносні величини структури характеризують склад досліджуваної сукупності, їх розраховують як відношення абсолютної величини кожного складового елементу до абсолютної величини всієї сукупності, тобто як відношення частини до цілого. Як правило, відносні величини структури виражаються у відсотках (база порівняння приймається за 100). Показники структури можуть бути виражені і в коефіцієнтній формі (база порівняння приймається за одиницю). Зіставляючи структуру одної і тої ж сукупності за різні періоди часу, можна простежити за структурними змінами. Відносні величини структури широко використовуються в аналізі підприємницької діяльності. За їх допомогою вивчають структуру випущеної продукції, структуру затрат на її виробництво, склад робітників підприємства за різними ознаками (статі, віку, стажу роботи). Відносними величинами координації називають співвідношення окремих частин певної сукупності між собою. Вони показують, у скільки разів зрівнювальна частина сукупності є більшою чи меншою від тої частини, яку взято за базу порівняння. Наприклад, у 1996 році чисельність міського населення України складала 34,8 млн. чоловік, а сільського - 16,5 млн. чоловік. Прийнявши за базу порівняння чисельність сільського населення України, розрахуємо відносну величину координації: 34,8: 16,5 = 2,1. Це означає, що чисельність міського населення України більше, ніж у два рази перевищує чисельність сільського населення. Відносні величини порівняння у просторі -це співвідношення одно-іменних величин різних об'єктів. Так, наприклад, можна зіставляти чисельність населення, розміри територій, величину посівних площ, обсяг промислової продукції між окремими країнами, областями, районами. Методику обчислення відносної величини порівняння в просторі розглянемо на такому прикладі. Станом на 1 січня 1996 року чисельність населення Києва складала 2630 тис., а Харкова- 1555 тисяч чоловік. Розрахуємо відносну величину порівняння у просторі, взявши за базу порівняння чисельність населення міста Харкова: 2630:1555=1,69. Отже, чисельність населення міста Києва в 1,69 раза більша від чисельності населення міста Харкова. Відносними величинами інтенсивності називаються показники, які характеризують ступінь поширення, розвиток явища у певному середовищі. За їх допомогою вимірюють інтенсивність його поширення, ступінь насиченості певного середовища даним явищем. Відносні величини інтенсивності завжди є відношенням двох різноіменних величин. За чисельник цього відношення береться величина явища (показник), ступінь поширення якого вивчається, а у знаменнику - величина того середовища, в якому розвивається (поширюється) це явище. Відносна величина інтенсивності показує, скільки одиниць однієї сукупності припадає на одиницю іншої сукупності. На відміну від інших видів відносних величин відносні величини інтенсивності завжди є величинами іменованими. Прикладом відносних величин інтенсивності може послужити показник, який характеризує кількість лікарів всіх спеціальностей в розрахунку на 10000 чоловік населення. Його розраховують шляхом ділення кількості лікарів всіх спеціальностей на загальну чисельність населення держави. Наприклад, кількість лікарів всіх спеціальностей в Україні станом на 1 січня 1996 року складала 230 тисяч чоловік. Загальна чисельність населення України на цю ж дату становила 51300 тис. чоловік. Отже, на кожних 10000 чоловік в Україні припадає 45,0 лікарів (230000-10000: 51300000). Ефективність використання статистичних показників у значній мірі залежить від дотримання ряду вимог і перш за все - врахування специфіки і умов розвитку суспільно-економічних явищ і процесів, а також комплексного застосування абсолютних і відносних величин в економіко-статистичних дослідженнях. Саме такий підхід забезпечує найбільш повне відображення досліджуваної дійсності. Важливою умовою правильного використання статистичних показників є вивчення явищ через застосування абсолютних і відносних величин у їх єдності. ТЕМА: СЕРЕДНІ ВЕЛИЧИНИ План.
Середня, її суть і види Серед узагальнюючих показників, що застосовуються для характеристики суспільних явищ і виявлення закономірностей їх розвитку, велике значення мають середні величини. Це пояснюється тим, що статистика вивчає сукупності за варіюючими ознаками, зміна яких проявляється у зміні їх кількісних значень в окремих одиниць цих сукупностей. На величину індивідуальних значень кожної одиниці спостереження діють декілька причин, певний вплив мають також і їх індивідуальні особливості. Наприклад, розподіл робітників двох підприємств можна охарактеризувати за їх кваліфікацією, яка виражається розрядом. Для цього слід розраховувати показник середнього тарифного розряду окремо по кожному підприємству. Одержані середні можна порівняти і дати однозначну відповідь, на якому з підприємств рівень кваліфікації робітників вищий. Рівень кваліфікації робітників, що досліджуються, одержує узагальнюючу характеристику у вигляді середньої величини. В середній величині виражається те типове, що характерне для всієї сукупності. Середня є одним з найбільш поширених способів узагальнення. Середньою величиною в статистиці називають узагальнюючий показник, який характеризує типовий рівень варіюючої ознаки в розрахунку на одиницю однорідної сукупності. Вивчаючи суспільні явища з метою виявлення характерних, закономірних рис в конкретних умовах місця і часу, статистика широко використовує середні величини. Важко без визначення середніх дати порівняльну характеристику продуктивності праці, рівня урожайності і ін. Важливість середніх величин для статистичної практики і науки відзначається в роботах багатьох вчених. Так, відомий англійський економіст В.Петті (1623-1687) пропонував широко використовувати середні величини при вивченні економічних проблем, зокрема, використовувати як міру вартості затрат на середнє денне харчування одного дорослого працівника. Він вважав стійкість середньої величини як відображення закономірностей явищ, що вивчаються, і його зовсім не хвилювало те, що дані по окремих робітниках не співпадають з середньою величиною. Значний вклад у розробку теорії середніх величин належить бельгійському вченому А.Кетле (1796-1874). Згідно Кегле на кожне явище діють як постійні (загальні), так і індивідуальні причини, причому перші роблять ці явища подібними одне до одного, стверджують загальні для всіх них закономірності. Наслідком вчення А.Кетле про загальні і індивідуальні причини стало виділення середніх величин як основного методу статистичного аналізу. Він підкреслював, що статистичні середні величини є не просто методом математичного вимірювання, а категорією об'єктивної дійсності. Типову, реально існуючу середню він ототожнював з істинною величиною, відхилення від якої можуть бути тільки випадковими. В підтвердження цьому є обгрунтована ним теорія «середньої людини». За його твердженням середня людина - це людина, наділена всіма рисами у середньому розмірі. Вона є середньою на зріст і вагу, має середню смертність і народжуваність, середній нахил до шлюбу і самогубства, до добрих і поганих справ і т.ін. Для Кегле «середня людина» не проста абстракція. Це ідеал людини. Проте помилковість теорії «середньої людини» Кегле була доказана ще в кінці минулого сторіччя. Відомий статистик Ю.Янсон писав, що Кегле передбачає існування в природі типу середньої людини як чогось даного, від якого життя відхилило «середніх людей» цього суспільства і даного часу, а це, природньо, приводить його до абсолютно механічного погляду і на закони руху соціального життя: рух - це не розвиток, а поступове зростання середніх властивостей людини, поступове відновлення типу; тому таке нівелювання всіх проявів життя соціального тіла, за якого всякий поступальний рух припиняється. Вірне розуміння суті середньої визначає її особливу значущість в умовах ринкової економіки, коли середня через взаємне погашення індивідуальних значень дозволяє виявити загальну тенденцію розвитку. Тому при тлумаченні суті середніх слід виходити із положень закону великих чисел і його значення для середніх. Закон великих чисел створює умови, щоб в середній проявлявся типовий рівень варіюючої ознаки. Сам же розмір цього рівня визначається зовсім не законом великих чисел, а суттю того явища, що характеризується середньою.
де X - степенева середня; X - рівень ознаки - варіант; n - число варіантів; m - показник ступеня середньої. Зміна значення степеня (m) середньої визначає її вид: при m = 1, середня арифметична; m = 0, середня геометрична; m = -1, середня гармонійна. m = -2, середня квадратична; m = -3, середня кубічна, їх формули мають такий вигляд: середня арифметична середня геометрична середня гармонійна середня квадратична середня кубічна Із степеневих середніх в статистиці найчастіше використовується середня арифметична, рідше - середня гармонійна, середня геометрична використовується тільки при обчисленні середніх темпів динаміки, а середня квадратична - при розрахунках показників варіації. Середня кубічна практично не використовується. Питання про те, який вид середньої необхідно використовувати в окремому випадку, вирішується шляхом конкретного аналізу сукупності, що вивчається. Вірну характеристику сукупності за варіюючою ознакою в кожному окремому випадку дає тільки певний вид середньої. Крім степеневих середніх, в статистиці використовують описові характеристики розподілу варіюючої ознаки - моду і медіану. Застосовуються вони для характеристики структури сукупності, тому їх ще називають структурними середніми. Застосування середніх повинне виходити із позицій діалектичного розуміння категорій загального і індивідуального, масового і одиничного. У кожному конкретному випадку слід пам'ятати про вимоги, які ставляться перед середніми, що визначаються. По-перше - це вимога визначення середньої на основі масових даних. Індивідуальні значення досліджуваної ознаки у окремих одиниць сукупності повинні бути різними. Щоб одержати науково обґрунтовану типову величину, слід обчислення середньої здійснювати за даними, до яких залучається якнайбільше одиниць цієї сукупності. При узагальненні масових фактів випадкові відхилення індивідуальних величин від загальної тенденції взаємно погашаються у середній величині. Ця вимога в статистиці пов'язує середні з законом великих чисел. По-друге - це вимога якісної однорідності, одноманітності сукупності, по якій визначається середня. Ця вимога полягає в тому, що не можна застосовувати середні до таких сукупностей, окремі частини яких підлягають різним законам розвитку відносно осереднюваної ознаки. Якщо, наприклад, визначити середню врожай-ність сільськогосподарських культур, то ніяк не можна її розраховувати, склав ши разом урожай зернових і технічних культур. Така середня не відобразить особливостей цього явища і буде не науковою, а фіктивною. Ось чому застосування методу середніх пов'язують з методом групування. Потрібно будь-яку досліджувану сукупність розчленувати спочатку на однорідні групи за певною ознакою, а вже потім визначати середню досліджуваної ознаки.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 689; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.137.10 (0.008 с.) |

 Середні, що застосовуються в статистиці, відносяться до класу степеневих середніх, формула яких має вигляд:
Середні, що застосовуються в статистиці, відносяться до класу степеневих середніх, формула яких має вигляд: ;
;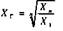 ;
;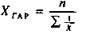 ;
;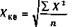 ;
; .
.


