
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: абсолютні та відносні величини.Содержание книги
Поиск на нашем сайте ТЕМА: АБСОЛЮТНІ ТА ВІДНОСНІ ВЕЛИЧИНИ. Види, значення і функції узагальнюючих статистичних показників Зібрані внаслідок статистичного спостереження первинні матеріали за допомогою зведення і групування узагальнюються, в результаті чого одержують зведені статистичні таблиці, в яких сукупності одиниць подаються в цілому та в розрізі груп. Показники, за допомогою яких статистика характеризує сукупності одиниць в цілому або її окремих груп, називаються узагальнюючими показниками. Узагальнюючі статистичні показники характеризують кількісно величину ознаки досліджуваної сукупності суспільних явищ в певних одиницях виміру. Статистичні показники виконують функції: пізнавальну, управлінську, контрольну, стимулюючу. Узагальнюючі статистичні показники служать базою для аналізу та прогнозування соціально-економічного розвитку держави, її окремих галузей і регіонів, стану і розвитку досліджуваних явищ, напряму і інтенсивності процесів, що проходять у суспільстві. Вивчаючи кількісну сторону явищ, економіст аналізує, пізнає її якісну сторону, проникає в її суть. У цьому і проявляється пізнавальна функція статистичних показників. Управлінська функціястатистичних показників полягає в тому, що вони є важливим елементом процесу управління на всіх його рівнях. З розвитком ринкових відносин ця роль статистичних показників зростає. Зростає і контрольна функція статистичних показників і, перш за все, за ходом виконання договірних умов. Серед показників, які розраховуються в практиці статистичної роботи, можна виділити три групи за такими ознаками: 1) за суттю досліджуваних явищ розрізняють показники об'ємні, що характеризують розміри явищ, процесів (обсяг виробництва, реалізації), і якісні, що характеризують кількісні співвідношення, характерні властивості досліджуваних явищ (наприклад, продуктивність праці); 2) за ступенем агрегування явищ можна виділити індивідуальні, що виражають розміри ознаки окремих одиниць сукупності, і загальні (узагальнюючі), що виражають розміри ознаки окремих груп або всієї сукупності; 3) залежно від характеру досліджуваних явищ розрізняють статистичні показники інтервальні, які виражають розміри кількісної ознаки за певні періоди часу (обсяг капітальних вкладень за місяць, квартал), і моментні, що виражають розміри кількісної ознаки на певний момент (дату), наприклад, запаси товарно-матеріальних ресурсів, спискова чисельність робітників на підприємстві. Для того, щоб статистичні показники правильно відображали досліджувані явища, необхідно дотримуватися таких вимог: 1) при їх побудові слід опиратися на положення економічної теорії та статистичну методологію їх побудови; 2) домагатися одержання повної інформації як за охопленням кількості одиниць сукупності, так і за кількістю сторін (ознак) досліджуваного явища; 3) забезпечити порівняльність статистичних показників в часі і просторі, в одиницях виміру; 4) забезпечити точність і достовірність вихідної інформації, на основі якої розраховуються показники. Статистичні показники, будучи відображенням об'єктивної дійсності, перебувають у тісному взаємозв'язку між собою. Тому розглядають їх не ізольовано один від одного, а в певному взаємозв'язку. Наприклад, для характеристики діяльності промислового підприємства необхідно розглядати декілька показників (обсяг виробництва, основні фонди і ін.), які, перебуваючи у певному взаємозв'язку, утворюють систему статистичних показників. Абсолютні статистичні величини і їх види Абсолютні величини -це показники, які виражають розміри суспільно-економічних явищ і процесів в конкретних умовах місця і часу. Одержують їх внаслідок статистичного спостереження і зведення вихідної інформації. Абсолютні величини широко використовуються у практиці підприємницької діяльності, в її аналізі і прогнозуванні. На їх основі складають господарські угоди, визначають обсяги попиту на окремі види виробів і їх виробництво. Джерелом формування статистичної інформації є абсолютні величини, за допомогою яких вимірюють всі сторони суспільного життя, їх значення в умовах формування ринкових відносин важко переоцінити. Сьогодні необхідно мати точну інформацію про ступінь збалансованості попиту покупців на конкретні товари з можливостями їх виробництва. За способом вираження розмірів досліджуваних явищ абсолютні величини поділяються на індивідуальні і загальні (підсумкові). Індивідуальні характеризують розміри кількісних ознак в окремих одиниць, наприклад, рівень виробітку окремого робітника за конкретний період. Підсумкові абсолютні величини характеризують розмір ознаки сукупності, одержаної від складання кількісних значень ознак окремих одиниць сукупності. Так, підсумовування посівної площі сільськогосподарських підприємств за даними річної звітності дозволяє одержати показник абсолютного її розміру в межах району, області і т.д. Отже, внаслідок зведення звітних даних промислових підприємств одержують сумарні абсолютні дані про чисельність робітників, суми виплаченої заробітної плати, про кількість і вартість виробленої продукції в розрізі окремих галузей і загалом по народному господарству. Абсолютні статистичні величини - числа іменовані. Вони завжди мають певну розмірність, певні одиниці вимірювання. Одиниці вимірювання - важливий елемент статистичного дослідження. Вони можуть бути простими, складними (наприклад, квт-год. спожитої електроенергії) і умовними (7000 -калорійне паливо). Залежно від різних причин і завдань аналізу застосовуються одиниці виміру: натуральні, вартісні і трудові. Натуральні одиниці вимірювання у більшості випадків відповідають природним або споживчим властивостям предмету і виражаються у фізичних одиницях вимірювання ваги, довжини тощо. Так, виробництво цукру в тоннах, рідких продуктів - у літрах, в декалітрах, взуття - у парах. У тих випадках, коли облік в одному з одиниць вимірювання не дає достатньої уяви про явище, воно може обліковуватися у двох одиницях вимірювання. Так, наприклад, шкіра обліковується у квадратних дециметрах і у вагових одиницях, скло - у квадратних метрах і за вагою і т.д. Одиниця вимірювання може бути виражена і сумою добутків двох різних вимірників. Так, наприклад, робота вантажного транспорту обліковується у тонно-кілометрах, які є добутком кількості перевезених тонн вантажів на відстань (кілометри). При виробництві однорідної, але неоднакової продукції вона може бути перерахована в умовно-натуральні одиниці. Суть такого перерахунку полягає в тому, що один з продуктів приймається за одиницю, решта прирівнюється до нього на основі розрахованих коефіцієнтів. Наприклад, якщо вагонобудівний завод виготовив 2000 чотиривісних вагонів і 4000 двовісних, то загальну кількість вагонів необхідно перерахувати у двовісні (2000 • 2 + 4000 = 8000), оскільки один чотиривісний вагон дорівнює за своєю місткістю двом двовісним. Однак умовно-натуральні одиниці вимірювання мають обмежене застосування, оскільки вони придатні лише для підсумовування однорідної продукції. Щодо різноіменної продукції, то тут загальний обсяг виробництва (реалізації) визначають у вартісному (грошовому) вираженні. Облік продукції у грошовому вираженні застосовується як спосіб обчислення наслідків виробництва і як спосіб вимірювання її вартості. А це необхідно тому, що сукупний суспільний продукт, валовий внутрішній продукт і валовий національний продукт визначають у вартісному вираженні. ТЕМА: СЕРЕДНІ ВЕЛИЧИНИ План.
Середня, її суть і види Серед узагальнюючих показників, що застосовуються для характеристики суспільних явищ і виявлення закономірностей їх розвитку, велике значення мають середні величини. Це пояснюється тим, що статистика вивчає сукупності за варіюючими ознаками, зміна яких проявляється у зміні їх кількісних значень в окремих одиниць цих сукупностей. На величину індивідуальних значень кожної одиниці спостереження діють декілька причин, певний вплив мають також і їх індивідуальні особливості. Наприклад, розподіл робітників двох підприємств можна охарактеризувати за їх кваліфікацією, яка виражається розрядом. Для цього слід розраховувати показник середнього тарифного розряду окремо по кожному підприємству. Одержані середні можна порівняти і дати однозначну відповідь, на якому з підприємств рівень кваліфікації робітників вищий. Рівень кваліфікації робітників, що досліджуються, одержує узагальнюючу характеристику у вигляді середньої величини. В середній величині виражається те типове, що характерне для всієї сукупності. Середня є одним з найбільш поширених способів узагальнення. Середньою величиною в статистиці називають узагальнюючий показник, який характеризує типовий рівень варіюючої ознаки в розрахунку на одиницю однорідної сукупності. Вивчаючи суспільні явища з метою виявлення характерних, закономірних рис в конкретних умовах місця і часу, статистика широко використовує середні величини. Важко без визначення середніх дати порівняльну характеристику продуктивності праці, рівня урожайності і ін. Важливість середніх величин для статистичної практики і науки відзначається в роботах багатьох вчених. Так, відомий англійський економіст В.Петті (1623-1687) пропонував широко використовувати середні величини при вивченні економічних проблем, зокрема, використовувати як міру вартості затрат на середнє денне харчування одного дорослого працівника. Він вважав стійкість середньої величини як відображення закономірностей явищ, що вивчаються, і його зовсім не хвилювало те, що дані по окремих робітниках не співпадають з середньою величиною. Значний вклад у розробку теорії середніх величин належить бельгійському вченому А.Кетле (1796-1874). Згідно Кегле на кожне явище діють як постійні (загальні), так і індивідуальні причини, причому перші роблять ці явища подібними одне до одного, стверджують загальні для всіх них закономірності. Наслідком вчення А.Кетле про загальні і індивідуальні причини стало виділення середніх величин як основного методу статистичного аналізу. Він підкреслював, що статистичні середні величини є не просто методом математичного вимірювання, а категорією об'єктивної дійсності. Типову, реально існуючу середню він ототожнював з істинною величиною, відхилення від якої можуть бути тільки випадковими. В підтвердження цьому є обгрунтована ним теорія «середньої людини». За його твердженням середня людина - це людина, наділена всіма рисами у середньому розмірі. Вона є середньою на зріст і вагу, має середню смертність і народжуваність, середній нахил до шлюбу і самогубства, до добрих і поганих справ і т.ін. Для Кегле «середня людина» не проста абстракція. Це ідеал людини. Проте помилковість теорії «середньої людини» Кегле була доказана ще в кінці минулого сторіччя. Відомий статистик Ю.Янсон писав, що Кегле передбачає існування в природі типу середньої людини як чогось даного, від якого життя відхилило «середніх людей» цього суспільства і даного часу, а це, природньо, приводить його до абсолютно механічного погляду і на закони руху соціального життя: рух - це не розвиток, а поступове зростання середніх властивостей людини, поступове відновлення типу; тому таке нівелювання всіх проявів життя соціального тіла, за якого всякий поступальний рух припиняється. Вірне розуміння суті середньої визначає її особливу значущість в умовах ринкової економіки, коли середня через взаємне погашення індивідуальних значень дозволяє виявити загальну тенденцію розвитку. Тому при тлумаченні суті середніх слід виходити із положень закону великих чисел і його значення для середніх. Закон великих чисел створює умови, щоб в середній проявлявся типовий рівень варіюючої ознаки. Сам же розмір цього рівня визначається зовсім не законом великих чисел, а суттю того явища, що характеризується середньою.
де X - степенева середня; X - рівень ознаки - варіант; n - число варіантів; m - показник ступеня середньої. Зміна значення степеня (m) середньої визначає її вид: при m = 1, середня арифметична; m = 0, середня геометрична; m = -1, середня гармонійна. m = -2, середня квадратична; m = -3, середня кубічна, їх формули мають такий вигляд: середня арифметична середня геометрична середня гармонійна середня квадратична середня кубічна Із степеневих середніх в статистиці найчастіше використовується середня арифметична, рідше - середня гармонійна, середня геометрична використовується тільки при обчисленні середніх темпів динаміки, а середня квадратична - при розрахунках показників варіації. Середня кубічна практично не використовується. Питання про те, який вид середньої необхідно використовувати в окремому випадку, вирішується шляхом конкретного аналізу сукупності, що вивчається. Вірну характеристику сукупності за варіюючою ознакою в кожному окремому випадку дає тільки певний вид середньої. Крім степеневих середніх, в статистиці використовують описові характеристики розподілу варіюючої ознаки - моду і медіану. Застосовуються вони для характеристики структури сукупності, тому їх ще називають структурними середніми. Застосування середніх повинне виходити із позицій діалектичного розуміння категорій загального і індивідуального, масового і одиничного. У кожному конкретному випадку слід пам'ятати про вимоги, які ставляться перед середніми, що визначаються. По-перше - це вимога визначення середньої на основі масових даних. Індивідуальні значення досліджуваної ознаки у окремих одиниць сукупності повинні бути різними. Щоб одержати науково обґрунтовану типову величину, слід обчислення середньої здійснювати за даними, до яких залучається якнайбільше одиниць цієї сукупності. При узагальненні масових фактів випадкові відхилення індивідуальних величин від загальної тенденції взаємно погашаються у середній величині. Ця вимога в статистиці пов'язує середні з законом великих чисел. По-друге - це вимога якісної однорідності, одноманітності сукупності, по якій визначається середня. Ця вимога полягає в тому, що не можна застосовувати середні до таких сукупностей, окремі частини яких підлягають різним законам розвитку відносно осереднюваної ознаки. Якщо, наприклад, визначити середню врожай-ність сільськогосподарських культур, то ніяк не можна її розраховувати, склав ши разом урожай зернових і технічних культур. Така середня не відобразить особливостей цього явища і буде не науковою, а фіктивною. Ось чому застосування методу середніх пов'язують з методом групування. Потрібно будь-яку досліджувану сукупність розчленувати спочатку на однорідні групи за певною ознакою, а вже потім визначати середню досліджуваної ознаки. Структурні середні величини Середні арифметична і гармонійна є узагальнюючими характеристиками сукупностей за тією чи іншою варіюючою ознакою. В той же час для характеристики структури цих сукупностей застосовуються особливі показники, які називають у статистиці структурними середніми. Зокрема, це мода і медіана., Мода (Мо) - це величина, яка найчастіше зустрічається в даній сукупності. У варіаційному ряді це буде варіант, що має найбільшу частоту. Мода широко використовується в комерційній діяльності, в соціологічних дослідженнях, коли вивчають ринковий попит, при реєстрації цін, встановленні рейтингу популярності осіб чи товарів і т. ін. Медіаною (Me) в статистиці називають варіант, що знаходиться в середині упорядкованого варіаційного ряду, тобто ділить його на дві рівні частини: одна частина має значення варіюючої ознаки менше, ніж середня, а друга - більше. Медіана показує величину варіюючої ознаки, якої досягла половина одиниць сукупності. Мода і медіана, на відміну від степеневих середніх є конкретними характеристиками варіаційного ряду, мають певні значення, тому їх ще називають описовими характеристиками, їх описовий характер пов'язаний з тим, що в цих величинах не погашаються індивідуальні відхилення, як це відбувається в середніх. Вони завжди відповідають повному варіанту. Мода і медіана не є типовими характеристиками в тих випадках, коли досліджуються сукупності однорідні і з великою чисельністю одиниць. Знайти моду і медіану в дискретному варіаційному ряді не складає труднощів. Тут значення варіантів мають певні числа. Інколи зустрічаються ряди розподілу, в яких не один, а два варіанти однаково модальні, тобто мають найбільші частоти. Це значить, що є дві моди, і розподіл тут бімодальний. Бімодальні розподіли вказують на якісну неоднорідність сукупності за досліджуваною ознакою. Отже, визначення моди і медіани в дискретному варіаційному ряді не викликає проблем. В інтервальному варіаційному ряді для визначення приблизного значення моди і медіани у межах певного інтервалу звертаються до спеціальних розрахунків, використовуючи для цього відповідні формули. Зокрема, для визначення певного значення модальної величини ознаки, що знаходиться в певному інтервалі, вона має такий вигляд:
де Х0 - нижня границя модального інтервалу; іm - величина модального інтервалу; Для визначення медіани з інтервального ряду використовується така формула:
де Хme - нижня границя медіанного інтервалу; і - величина медіанного інтервалу; Sme - сума нагромаджених (кумулятивних) частот до медіанного інтервалу; ТЕМА: АБСОЛЮТНІ ТА ВІДНОСНІ ВЕЛИЧИНИ.
|
||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.013 с.) |

 Середні, що застосовуються в статистиці, відносяться до класу степеневих середніх, формула яких має вигляд:
Середні, що застосовуються в статистиці, відносяться до класу степеневих середніх, формула яких має вигляд: ;
;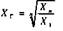 ;
;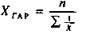 ;
;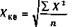 ;
; .
.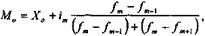
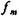 - частота модального інтервалу;
- частота модального інтервалу; 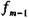 - частота інтервалу, що передує модальному;
- частота інтервалу, що передує модальному;  - частота інтервалу, що іде за модальним інтервалом.
- частота інтервалу, що іде за модальним інтервалом.



