
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Середня гармонійна та умови її застосуванняСодержание книги
Поиск на нашем сайте
Статистичні середні завжди виражають якісні властивості суспільних явищ і процесів. В процесі досліджень важливо правильно вибрати форму середньої, яка б відповідала природі взаємозв'язків явищ і їх ознак. Поряд із середньою арифметичною в статистичних дослідженнях використовують інші види, зокрема, середню гармонійну. За своїми властивостями середня гармонійна може застосовуватись тоді, коли загальний обсяг ознаки формується як сума зворотних значень варіантів. Таких випадків у сфері соціально-економічних явищ зустрічається відносно мало. Проте, не дивлячись на це, середня гармонійна застосовується в статистиці досить широко. До неї звертаються тоді, коли ваги (тобто добуток варіантів на частоти) ділять на варіанти, або це те ж саме, що множать на зворотнє їм число. Таким чином, середня гармонійна - це величина зворотня середній арифметичній із зворотніх значень ознаки. Звернемося до прикладу. Розрахунок середніх затрат часу, необхідного для виготовлення однієї деталі в бригаді токарів, що виробляють цю продукцію, здійснюється відношенням: Формула середньої гармонійної простої має такий вигляд:
- зворотні значення варіантів.
Структурні середні величини Середні арифметична і гармонійна є узагальнюючими характеристиками сукупностей за тією чи іншою варіюючою ознакою. В той же час для характеристики структури цих сукупностей застосовуються особливі показники, які називають у статистиці структурними середніми. Зокрема, це мода і медіана., Мода (Мо) - це величина, яка найчастіше зустрічається в даній сукупності. У варіаційному ряді це буде варіант, що має найбільшу частоту. Мода широко використовується в комерційній діяльності, в соціологічних дослідженнях, коли вивчають ринковий попит, при реєстрації цін, встановленні рейтингу популярності осіб чи товарів і т. ін. Медіаною (Me) в статистиці називають варіант, що знаходиться в середині упорядкованого варіаційного ряду, тобто ділить його на дві рівні частини: одна частина має значення варіюючої ознаки менше, ніж середня, а друга - більше. Медіана показує величину варіюючої ознаки, якої досягла половина одиниць сукупності. Мода і медіана, на відміну від степеневих середніх є конкретними характеристиками варіаційного ряду, мають певні значення, тому їх ще називають описовими характеристиками, їх описовий характер пов'язаний з тим, що в цих величинах не погашаються індивідуальні відхилення, як це відбувається в середніх. Вони завжди відповідають повному варіанту. Мода і медіана не є типовими характеристиками в тих випадках, коли досліджуються сукупності однорідні і з великою чисельністю одиниць. Знайти моду і медіану в дискретному варіаційному ряді не складає труднощів. Тут значення варіантів мають певні числа. Інколи зустрічаються ряди розподілу, в яких не один, а два варіанти однаково модальні, тобто мають найбільші частоти. Це значить, що є дві моди, і розподіл тут бімодальний. Бімодальні розподіли вказують на якісну неоднорідність сукупності за досліджуваною ознакою. Отже, визначення моди і медіани в дискретному варіаційному ряді не викликає проблем. В інтервальному варіаційному ряді для визначення приблизного значення моди і медіани у межах певного інтервалу звертаються до спеціальних розрахунків, використовуючи для цього відповідні формули. Зокрема, для визначення певного значення модальної величини ознаки, що знаходиться в певному інтервалі, вона має такий вигляд:
де Х0 - нижня границя модального інтервалу; іm - величина модального інтервалу; Для визначення медіани з інтервального ряду використовується така формула:
де Хme - нижня границя медіанного інтервалу; і - величина медіанного інтервалу; Sme - сума нагромаджених (кумулятивних) частот до медіанного інтервалу;
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 345; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.227.108 (0.005 с.) |


 Вона використовується в тому випадку, коли обсяг явищ, тобто добутки по кожній ознаці рівні. У тих випадках, коли ці добутки по кожній ознаці нерівні, використовується середнягармонійна зважена, яка має такий вигляд:
Вона використовується в тому випадку, коли обсяг явищ, тобто добутки по кожній ознаці рівні. У тих випадках, коли ці добутки по кожній ознаці нерівні, використовується середнягармонійна зважена, яка має такий вигляд: де W - добуток варіанта на частоту (Xf), звідси
де W - добуток варіанта на частоту (Xf), звідси 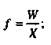
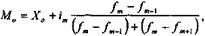
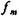 - частота модального інтервалу;
- частота модального інтервалу; 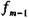 - частота інтервалу, що передує модальному;
- частота інтервалу, що передує модальному;  - частота інтервалу, що іде за модальним інтервалом.
- частота інтервалу, що іде за модальним інтервалом.



