Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение относительных величин. Виды относительных величин.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Наряду с абсолютными статистическими величинами большое значение в статистике имеют относительные величины. В процессе выявления ряда важнейших для социально-экономической жизни вопросов возникает необходимость в изучении структуры явления, соотношения между отдельными его частями, развития во времени. Относительная величина в статистике — это обобщающий показатель, который представляет собой частное от деления одного абсолютного показателя на другой и дает числовую меру соотношения между ними. Основное условие правильного расчета относительной величины — сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Величина, с которой производится сравнение (знаменатель дроби), обычно называется базой сравнения или основанием. В зависимости, от выбора базы сравнения относительный показатель может быть представлен в различных долях единицы: десятых; сотых (т. е. процентах); тысячных (десятая часть процента называется промилле); десятитысячных (сотая часть процента называется продецимилле). По своему содержанию относительные величины подразделяются на виды: относительные величины динамики, планового задания, структуры, интенсивности, уровня экономического развития, координации и сравнения. 1). Относительная величина динамики - она характеризует изменение уровня какого-либо явления во времени и показывает во сколько раз увеличился (или уменьшился) уровень показателя по сравнению с предшествующем периодом. Различают относительные показатели динамики с постоянной и переменной базой сравнения. Если сравнение осуществляется с одним и тем же базисным уровнем (например, с первым годом рассматриваемого периода), то получают относительные показатели динамики с постоянной базой (базисным). Если сравнение осуществляется с предшествующим уровнем, то получают показатели динамики с переменной базой (цепным)
Если данный показатель выраженный в кратком отношении, он называется коэффициентом роста при умножении на 100% получают темп роста. 2). Относительная величина выполнения плана отражает фактический уровень показателя в процентах или коэффициентах по сравнению с плановым уровнем. Она хар-ет степень выполнения плана. 3). Относительная величина планового задания характеризует напряженность планового задания. Она показывает на сколько планируется увеличить (или уменьшить) уровень показателя в текущем периоде по сравнению с фактически достигнутым уровнем предшествующего периода.
4). Относительными величинами структуры называются показатели, характеризующие долю отдельных частей изучаемой совокупности во всем ее объеме. 5) Относительная величина координации характеризует соотношение между частями одного целого. Она показывает во сколько раз одна часть совокупности больше другой или сколько единиц одной части приходится на 1, 10, 100…1000 и т. д. единиц другой части. 6). Относительная величина интенсивности называют показатель, характеризующий степень распространения или уровень развития того или иного явления в определенной среде. Они вычисляются путем сравнения разноименных величин, находящихся в определенной связи между собой. Эти показатели обычно определяются в расчете на 100, 1000 и т.д. единиц изучаемой совокупности (на 100 га земли, на 1000 человек населения и т.д.) и являются именованными числами. 7) Относительная величина сравнения характеризует сравнительные размеры одноименных абсолютных величин относящихся к одному и тому же периоду или моменту времени, но к различным объектам или территориям. 4. ПОНЯТИЕ О СРЕДНИХ ВЕЛЕЧИНАХ. Средней величиной в статистике называется обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин. Вычисление среднего — один из распространенных приемов обобщения; средний показатель отражает то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае. В способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей. Там, где возникает потребность обобщения, расчет таких характеристик приводит к замене множества различных индивидуальных значений признака средним показателем, характеризующим всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях. Средняя отражает характерный, типичный, реальный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и в пространстве. Средняя — это сводная характеристика закономерностей процесса в тех условиях, в которых он протекает. Анализ средних выявляет, например, закономерности изменения производительности труда, заработной платы рабочих отдельного предприятия на определенном этапе его экономического развития, изменения климата в конкретном пункте земного шара на основе многолетних наблюдений средней температуры воздуха и др. Однако для того, чтобы средний показатель был действительно типизирующим, он должен определяться не для любых совокупностей, а только для совокупностей, состоящих из качественно однородных единиц. Это является основным условием научно обоснованного использования средних. Средние, полученные для неоднородных Совокупностей, будут искажать характер изучаемого общественного явления, фальсифицировать его, или будут бессмысленными. Так, если рассчитать средний уровень доходов служащих какого-либо района, то получится фиктивный средний показатель, поскольку для его исчисления использована неоднородная совокупность, включающая в себя служащих предприятий различных типов (государственных, совместных, арендных, акционерных) i а также органов государственного управления, сферы науки, культуры, образования и т.п. В таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и исчисляются типические групповые средние. Групповые средние позволяют избежать "огульных" средних, обеспечивают сравнение уровней отдельных групп с общим уровнем по совокупности, выявление имеющихся различий и т.д. ВИДЫ СРЕДНИХ И СПОСОБЫ ИХ ВЫЧИСЛЕНИЯ. Выбор вида средней определяется экономическим содержанием определенного показателя и исходных данных. В каждом конкретном случае применяется одна из средних величин: арифметическая, гармоническая, геометрическая, квадра-» тическая, кубическая и т.д. В зависимости от значения показателя степени т различают следующие виды степенных средних:при т = -1 — средняя гармоническая Хгар; при т = О — средняя геометрическая хг; при т = 1 — средняя арифметическая хар; при от = 2 — средняя квадратическая хкв; при т = 3 — средняя кубическая хкуб При использовании одних и тех же исходных данных, чем больше т в формуле (5.1), тем больше значение средней величины:
Это свойство степенных средних возрастать с повышением 1 показателя степени определяющей функции называется в стати-I* стике правилом мажорантности средних. Характер имеющихся данных определяет существование только одного истинного среднего значения показателя. Вид средней выбирается в каждом отдельном случае путем конкретного анализа изучаемой совокупности, он определяется материальным содержанием изучаемого явления, а также принципами суммирования и взвешивания. Помимо степенных средних в статистической практике используются средние структурные, в качестве которых рассматриваются мода и медиана. СРЕДНЯЯ АРИФМЕТИЧЕСКАЯ. Наиболее распространенным видом средних является средняя арифметическая. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Для общественных явлений характерна аддитивность (суммарность) объемов варьирующего признака, этим определяется область применения средней арифметической и объясняется ее распространенность как обобщающего показателя. Так, например, общий фонд заработной платы — это сумма заработных плат всех работников, валовой сбор урожая - сумма произведенной продукции со всей посевной площади.Чтобы исчислить среднюю арифм-ую, нужно сумму всех значений признаков разделить на их число.Средняя арифметическая применяется в форме простой средней и взвешенной средней. Исходной, определяющей формой, служит простая средняя. Средняя арифметическая простая равна простой сумме отдельных значений осредняемого признака, деленной на общее число этих значений:
где X1,X2...Xn- индивидуальные значения варьирующего признака (варианты); n- число единиц совокупности. Средняя арифметическая взвешенная — средняя сгруппированных величин— вычисляется по формуле:
Тогда формула взвешенной будет иметь вид: X‾ap=∑xd / ∑d где d =f / ∑f— частость, т.е. доля каждой частоты в общей сумме всех частот. Если частоты подсчитывают в долях (коэфф-тах), то ∑d=1и формула средней арифметической взвешенной имеет вид: Часто приходится исчислять среднюю по групповым средним или по средним отдельных частей совокупности (частным средним), т.е. среднюю из средних. Так, например, средняя продолжит-ть жизни граждан страны представляет собой среднее из средних продолж-ей жизни по отдельным регионам данной страны. Средние из средних рассчитываются так же, как и средние из первоначальных значений признака. При этом средние, которые служат для исчисления на их основе общей средней, принимаются в качестве вариантов. Вычисление средней арифметической взвешенной из групповых средних X‾гр осуществляется по формуле: X‾ap=∑X‾грf / ∑f где f— число единиц в каждой группе. Расчет средней арифметической в рядах распределения: Если значения осредняемого признака заданы в виде интервалов ("от — до"), т.е. интервальных рядов распределения, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд. Свойства средней арифмет-ой: 1) Если все индивидуальные значения признака (т.е. все варианты) уменьшить или увеличить в i раз, то среднее значение нового признака соответственно уменьшится или увеличится в i раз. 2). Если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А. 3) Если веса всех осредняемых вариантов уменьшить или увеличить в к раз, то средняя арифметическая не изменится. Для получения действительной средней надо момент первого порядка от, умножить на i и прибавить А:
Данный способ вычисления средней арифмет-ой из вариационного ряда называют «способом моментов». Применяется этот способ в рядах с равными интервалами. СРЕДНЯЯ ГАРМОНИЧЕСКАЯ. При расчете средних показателей помимо средней арифметической могут использоваться и другие виды средних. Однако любая средняя величина должна вычисляться так, чтобы при замене ею каждого варианта осредняемого признака не изменялся итоговый, обобщающий, или, как его принято называть, определяющий показатель, который связан с осредняемым показателем (например, при замене фактических скоростей на отдельных отрезках пути их средней скоростью не должно измениться общее расстояние, пройденное транспортным средством за одно и то же время; при замене фактических заработных плат отдельных работников предприятия средней заработной платой не должен измениться фонд заработной платы). Следовательно, в каждом конкретном случае в зависимости от характера имеющихся данных существует только одно истинное среднее значение показателя, адекватное свойствам и сущности изучаемого социально-экономического явления. Вид средней определяется характером взаимосвязи определяющего показателя с осредняемым. Формула средней гармонической взвешенной:
Из формулы видно, что средняя гармоническая — средняя взвешенная из варьирующих обратных значений признака. Она является преобразованной формой арифметической средней и тождественна ей. Таким образом, средняя гармоническая применяется тогда, когда неизвестны действительные веса f, а известно w=x*fт.е. в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, когда суммированию подлежат не сами варианты, а обратные им величины.___В тех случаях, когда вес каждого варианта равен единице (индивидуальные значения обратного признака встречаются по одному разу), применяется средняя гармоническая простая, исчисляемая по формуле:
где 1/x— отдельные варианты обратного признака, встречающиеся по одному разу; п — число вариантов.__Если по двум частям совокупности даны средние гармонические, то общую среднюю гармоническую по всей совокупности можно представить как взвешенную гармоническую среднюю из групповых средних:
Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана. Мода M0 — значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду — вариант, имеющий наибольшую частоту. В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:
где XM0— нижняя граница модального интервала; iM0 — модальный интервал;— частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно). Модальный интервал определяется по наибольшей частоте. Мода широко используется в статист-ой практике при изучении покупательского спроса, регистрации цен и т.п. Медиана Мe — это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части — со значениями признака меньше медианы и со значениями признака больше медианы. Чтобы найти медиану, необходимо отыскать значение признака, которое находится в середине упорядоченного ряда. В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы. Значение медианы вычисляется линейной интерполяцией по формуле:
где XMe- нижняя граница медианного интервала; iMe — медианный интервал; ∑f / 2 — половина от общего числа наблюдений; SM e-1 сумма наблюдений, накопленная до начала медианного интервала; fMe- число наблюдений в медианном интервале. Медиана находит практическое применение в маркетинговой деятельности вследствие особого свойства — сумма абсолютных отклонений чисел ряда от медианы есть величина наименьшая: ∑ (x-Me) →min. Мода и медиана в отличие от степенных средних являются конкретными харак-ми, их значение имеет какой—либо конкретный вариант в вариационном ряду. Мода и медиана, как правило, отличаются от значения средней, совпадая с ней только в случае симметричного распределения частот вариационного ряда. Поэтому соотношение моды, медианы и средней арифметической позволяет оценить ассиметрию рада распределения. Мода и медиана, как правило, являются допол-ми к средней характ-ми совокупности и используются в математической статистике для анализа формы рядов распределения. Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные (по числу единиц) части — квартели, на пять равных частей - квттели, на десять частей - децели, на сто частей — перцентели. Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет более глубоко и детально охарактеризовать изучаемую совокупность. СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ применяется в тех случаях, когда индивидуальные значения признака представляют собой, как правило, относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста. Средняя геометрическая исчисляется извлечением корня степени п из произведений отдельных значений — вариантов признака х. где n - число вариантов; П - знак произведения. Наиболее широкое применение средняя геом-ая получила для определения средних темпов изменения в рядах динамики, а также в рядах распределения. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ И СРЕДНЯЯ КУБИЧЕСКАЯ. В ряде случаев в экономической практике возникает потребность расчета среднего размера признака, выраженного в квадратных или кубических единицах измерения. Тогда применяется средняя квадратическая (например, для вычисления средней величины стороны и квадратных участков, средних диаметров труб, стволов и т.п.) и средняя кубическая (например, при определении средней длины стороны л кубов). Формулы для расчета средней квадратической: Средняя квадратическая простая является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 3252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.61 (0.009 с.) |

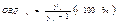 ;
;  , где
, где  - это уровень показателей в текущем (отчетном периоде),
- это уровень показателей в текущем (отчетном периоде),  - это уровень показателей в предшествующем периоде,
- это уровень показателей в предшествующем периоде,  - это уровень показателей в базисном периоде.
- это уровень показателей в базисном периоде. , где
, где  -это фактический уровень показателя в отчетном периоде,
-это фактический уровень показателя в отчетном периоде,  -это планируемый уровень показателя на отчетный период.
-это планируемый уровень показателя на отчетный период.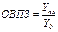 , где
, где 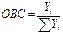 , где
, где  - это показатель характеризующий i часть совокупности, сумма
- это показатель характеризующий i часть совокупности, сумма  , где
, где  - это уровень показателей хар-щий часть совокупности выбранную в качестве базы сравнения.
- это уровень показателей хар-щий часть совокупности выбранную в качестве базы сравнения.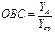 , где
, где  - это показатель характер-ий явления А,
- это показатель характер-ий явления А,  - это показатель хар-ий среду распространения явления А.
- это показатель хар-ий среду распространения явления А. , где
, где  - показатель хар-ий объект Б.
- показатель хар-ий объект Б.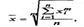 Перечисленные средние относятся к классу стеленных средних § и объединяются общей формулой* (при различных значениях т): где х - среднее значение исследуемого явления; т — показатель степени средней; х — текущее значение (вариант) осредняемого признака; и - число признаков.
Перечисленные средние относятся к классу стеленных средних § и объединяются общей формулой* (при различных значениях т): где х - среднее значение исследуемого явления; т — показатель степени средней; х — текущее значение (вариант) осредняемого признака; и - число признаков.