
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6, 7. Средние величины. Показатели вариацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель: углубление знаний о средних величинах как обобщающих показателях, выражающих типичные размеры количественно варьирующих признаков качественно однородных массовых общественных явлений и процессов. Вариация - колеблемость признака. Понятие сущности вариации и значение ее исследования. Применение показателя вариации для характеристики однородности совокупности и типичности средней величины. Основные вопросы занятия: 1. Вариация массовых явлений и средние величины. Их сущность и значение. 2. Виды средних величин и техника их вычисления. 3. Мода и медиана - показатели центра распределения. Расчет моды и медианы в дискретном и интервальном рядах распределения. 4. Способы расчета показателей вариации. Методические указания к решению задач В статистике применяют несколько видов средних величин: арифметическую, гармоническую, геометрическую, хронологическую, квадратическую, кубическую и др. В зависимости от частоты повторения вариант средние вычисляются как простые (не взвешенные) и взвешенные. Средняя применена правильно, если в результате получают величины, имеющие реальный экономический смысл. Средняя должна рассчитываться по качественно однородной совокупности, иначе она будет фиктивной. Виды средних величин Выбор формулы расчета средней величины зависит только от наличия исходных данных. 1. Средняя арифметическая применяется, если известны значения осредняемого признака Х и число единиц совокупности с этим значением X. Если каждая варианта - Х встречается 1 раз, то применяется средняя арифметическая простая:
где
Средняя арифметическая простая, как правило, применяется, если исходные данные не упорядочены. Если каждая варианта - Х встречается несколько раз, то применяется средняя арифметическая взвешенная:
где Средняя арифметическая взвешенная применяется, если задан упорядоченный ряд распределения, когда объем варьирующего признака для всей совокупности определяется как сумма значений признаков отдельных величин. Средняя гармоническая Средняя гармоническая применяется, когда неизвестна частота, но известны произведения варианты на частоту Средняя гармоническая вычисляется из обратных значений осредняемого признака и по форме может быть простой и взвешенной.
Средняя гармоническая простая рассчитывается по формуле:
Средняя гармоническая взвешенная
где Средняя геометрическая. Средняя геометрическая простая рассчитывается по формуле:
где x1, x2,..., xn - значения цепных коэффициентов роста; П - знак перемножения Средняя геометрическая взвешенная рассчитывается по формуле:
Применяется, если задана последовательность цепных относительных величин динамики, указывающих, например, на рост объема производства или снижение уровня преступности по сравнению с уровнем предыдущего года. Средняя хронологическая Средняя хронологическая применяется когда значения признака Х заданы на несколько дат внутри периода. Формула средней хронологической простой:
где, n - число дат, на которые известны значения Х.
(32) где, Xi и Xi+1 – значение уровня моментного ряда динамики и уровня, следующего за ним; fi – промежуток времени между датами Для изучения внутреннего строения совокупности применяют структурные средние - моду и медиану. Мода (
где
Медиана (
где Для дискретного ряда с четным числом медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда:
Для интервального вариационного ряда медиана определяется по формуле:
где
Не каждая средняя величина является объективной характеристикой изучаемой совокупности. Для расчета типичности средней, колеблемости признака применяются показатели вариации. Показатели вариации Колеблемость, изменяемость величины признака у единиц совокупности называется вариацией. Для характеристики вариационного ряда рассчитываются показатели вариации: 1. Размах вариации (R) - разница между наибольшим и наименьшим значением признака
2. Среднее линейное отклонение (d) - средняя арифметическая из абсолютных значений отклонений вариант от средней величины: · простое
3. Наиболее распространенным показателем вариации является среднее квадратическое отклонение
где
Дисперсия – это средняя из квадратов отклонений вариант от средней. Она не имеет единиц измерения. Среднее квадратическое отклонение имеет ту же единицу измерения, что и значение Х и показывает, как в среднем конкретные значения Х отклоняются в ту или иную сторону от среднего значения: Чем больше отклонение, тем менее типична средняя. 4. Коэффициент вариации характеризует колеблемость признака, однородность (неоднородность), совокупность, типичность (нетипичность) средней величины.
Если коэффициент вариации менее 10% - вариация слабая, совокупность однородная, средняя типична. Если коэффициент вариации находится в пределах от 10 до 33% - вариация умеренная, совокупность однородная, средняя типична. Если коэффициент вариации находится в пределах от 33 до 60% - вариация признака сильная, совокупность не однородная, средняя не типична. Если коэффициент вариации от 60 до 100% - вариация очень сильная, совокупность качественно неоднородная и средняя не является типичной характеристикой совокупности. Для расчета показателей вариации используют вспомогательную таблицу. Таблица 1. Расчет показателей вариации
Для характеристики ряда распределения рассчитывают: · коэффициент асимметрии
· коэффициент эксцесса
Задачи для практических занятий и самостоятельного решения Задача 23 Определить среднюю зарплату одного рабочего, моду и медиану, дисперсию, среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации.
Задача 24 На основании данных таблицы определите среднедневную выработку рабочих, моду, медиану, показатели вариации:
Задача 25 Рабочие завода «Теплоход» распределены по возрасту следующим образом:
Определите: средний возраст рабочих, моду, медиану, дисперсию, среднее квадратическое отклонение, коэффициенты вариации, концентрации и ассиметрии. Задача 26 По следующим данным определите среднюю величину каждого показателя по трем бригадам вместе:
Задача 27 Имеются данные о количестве произведенной продукции заводом ежемесячно в 2003г. (млн. руб.): I – 2,0; II – III – 2,3; IV – VI – 2,4; VII – XII – 2,7. Определите среднемесячный объем производства продукции за год. Задача 28 Имеются следующие данные о запасах материалов на начало месяца (тыс. руб.):
Вычислите среднемесячный запас материалов за полугодие. Задача 29 Имеются следующие данные об остатках полуфабрикатов в цехе:
Вычислите среднемесячные остатки полуфабрикатов: 1) за 3-й квартал; 2) за 4-й квартал; 3) за 2-е полугодие. Задача 30 Имеются данные о производстве продукции малых предприятий района, млн. руб.; 20,32,45,52,29,28,38,57,70,48,39,33,43,42,48,51,44,65,54,36,64,27,31,34,55,56,45,47,47,49,65,35,45, 48,53,54,58,57,62,63 1. Постройте ряд распределения предприятий по объему производства продукции, образовав пять групп с равными интервалами. 2. По данным ряда распределения определите: а) структуру предприятий по объему производства продукции; б) средний объем продукции на одно предприятие; в) дисперсию и среднее квадратическое отклонение; г). коэффициент вариации; д) структурные средние: моду и медиану. 3. Постройте график ряда распределения и покажите на нем исчисленные средние показатели. Сделайте выводы. Задача 31 По следующим данным о кредитных вложениях в экономику России в текущем году (млрд. руб.) определите: средний размер кредитных вложений по всей совокупности и по видам кредитов, показатели вариации и структуры. Сделайте выводы. Исходные данные:
Тема 8. Ряды динамики Динамика- это изменение явления во времени. Ряд динамики – это ряд расположенных в хронологическом порядке значений статистических показателей. Если данные представлены по состоянию на конкретный момент времени, то ряд динамики называется моментным. Если уровни ряда представляют результат за определенные периоды времени, то ряд называется интервальным. Абсолютные приросты (снижение) - D, темпы роста (снижения) – Tp и темпы прироста (снижения) - Tпр, могут быть рассчитаны с переменной базой сравнения – по отношению к предыдущему периоду (цепные) и постоянной базой сравнения (базисные) – к начальному уровню ряда. Абсолютные приросты · цепные
· базисные
Коэффициенты роста: · цепные
· базисные
Темпы роста: · цепные
· базисные
Темпы прироста: · цепные
· базисные
Средние показатели ряда динамики: 1. Средний уровень ряда исчисляется по формуле средней арифметической простой:
т.е. средний уровень ряда равен сумме уровней ряда, деленной на их число. Средний уровень моментного ряда динамики на равноотстоящие даты (с равными интервалами) определяется по формуле средней хронологической:
где п– число уровней ряда динамики. 2. Средний абсолютный прирост исчисляется двумя способами: а) как средняя арифметическая простая цепных приростов:
б) делением базисного прироста на число периодов:
3. Средний темп роста: 1 способ:
2 способ:
Абсолютное значение одного процента прироста: 1 способ:
2 способ:
Пункты роста– это разница между двумя соседними темпами роста:
Задачи для самостоятельного решения. Задача 32 Имеются следующие статистические данные о рождаемости за 2008-2012 гг.
Для анализа рождаемости за 2008-2012 гг. определите: 1. Абсолютные и относительные изменения рождаемости за каждый год (цепные) и к 2008 г. (базисные). 2. Полученные показатели представьте в таблице. 3. Среднегодовой уровень рождаемости 4. Среднегодовой темп рождаемости 5. Ожидаемое число родившихся в 2013, 2014, 2015 гг. при условии, что среднегодовой темп рождаемости предыдущего периода сохранится за эти годы. 6. Показатели прогноза представьте в общей таблице и вычислите все показатели, указанные в пункте 1. 7.Постройте график динамики рождаемости за 2008-2012 гг. 8. Проанализируйте показатели. Задача 33 Краткосрочные кредитные вложения в регионе за второе полугодие характеризуются данными:
По данным хронологического ряда определите: 1. Абсолютные приросты, темпы роста и прироста – базисные и цепные, абсолютное содержание 1 % прироста. Полученные показатели представьте в таблице. 2. Средний размер кредитных вложений за полугодие 3. Средний абсолютный прирост 4. Средний темп роста и прироста 5. Покажите взаимосвязь между цепными и базисными темпами роста. Спрогнозируйте уровни кредитных вложений в первом квартале следующего года, если среднегодовой темп роста в этом периоде снизился на 4,6 пункта по сравнению с предыдущим. 6. Постройте график динамики кредитных вложений за исследуемый период. Задача 34 Изменение средних остатков задолженности по кредиту характеризуется следующими данными:
Определить цепной темп роста и среднегодовой темп прироста средних остатков задолженности по кредиту. Задача 35 Дан интервальный ряд динамики
1. Построить таблицу 2. Построить линейную диаграмму 3. Найти все средние показатели динамики. Задача 36 Имеются следующие данные:
1. Определите индексы сезонности оседания вкладов за четыре года методом четырехчленной скользящей средней. 2. Постройте график сезонной волны. Задача 37
Найти: 1. Все показатели динамики, если в 2009 г. Y=600 2. Все средние величины. Задача 38
Найти все показатели динамики и средние величины. Задача 39
Найти: 1. Все показатели динамики, если на 01.12.2011 у=250 2. Все средние Задача 40 Дан ряд динамики
Найти все показатели динамики, проверить формулы связи Кбазисный и Кцепной.. Задача 41 Имеются данные о продаже яблок на рынке города (в тоннах)
1. Найти индексы сезонности (записать в таблицу), сезонную волну. 2. Взять данные за все 3 года, построить новый ряд, построить линейную диаграмму, найти 3. Методом скользящей средней (3 звена) выровнять ряд, построить график. Задача 42 Имеются данные о продаже томатов на рынке города (в тоннах)
1. Найти индексы сезонности (записать в таблицу), сезонную волну. 2. Значения уза все 3 года выровнять методом скользящей средней (3 звена), построить графики 3. Найти Задача 43 Среднегодовые темпы роста продукции фермерского хозяйства за период 2008-2012 гг. в земледелии составили 102,6%, а в животноводстве – 105,3%. Величина продукции в 2008 г. (в условных единицах) составила: в земледелии – 7820, в животноводстве – 8590. Определите среднегодовой темп роста продукции в целом за период 2008-2012 гг. Задача 44 Имеются следующие данные об объеме пассажирооборота по автобусным предприятиям города:
Вычислить и проставить в таблицу уровни ряда динамики и недостающие показатели динамики. Задача 45 На основе следующих отчетных данных по грузовому автотранспортному предприятию выявить тенденцию и прогноз объема перевозок на 2013г. методом среднего абсолютного прироста, среднего коэффициента роста, экстраполяционный прогноз методом аналитического выравнивания ряда.
Задача 46 По грузовому автотранспортному предприятию имеются следующие данные об объеме перевозок:
На основе приведенных данных требуется: 1) выявить наличие сезонной неравномерности; 2) определить величину сезонной волны, используя индексы сезонности. Задача 47 Известны темпы роста инвестиций по двум регионам (в % к 2009г.)
Определить темпы роста инвестиций за каждый год по сравнению с предшествующим годом и среднегодовые темпы роста инвестиций для каждого региона. Сформулируйте вывод. Задача 48 Имеются следующие данные о численности студентов высших учебных заведений России (на конец учебного года, тыс. чел.). Исчислить отсутствующие в таблице сведения о численности студентов за 2008 - 2012гг. Проанализировать динамику изучаемого явления, опираясь на рассчитанные показатели динамики.
Задача 49 По данным о перевозке грузов речным пароходством определить недостающие уровни и цепные показатели динамики:
Задача 50 Выработка изделия на предприятии в 2004г. составила 4 тыс. шт., в 2007г. 4.6 тыс. шт., в 2008г.-5 тыс.шт. Определить методом интерполяции выработку изделия в 2003 и 2006 г.г. Задача 51 Среднее расстояние перевозки грузов в международном сообщении по годам характеризуется следующими данными:
Произвести аналитическое сглаживание с последующей экстраполяцией для 2013г. Задача 52 Имеются следующие данные о ежесуточной добыче угля по шахте за первую декаду:
Произвести сглаживание ряда методом трехчленной переменной и трехчленной скользящей средней. Дать график первичного и сглаженного рядов. Задача 53 Производство цемента в регионе характеризуется следующими данными:
Провести выравнивание по прямой и использовать полученное уравнение для экстраполяции уровней 2013 и 2014 гг. Построить график первичного и выровненного рядов. Какой агрегатный индекс физического объема можно найти? Найдите его. Тема 9. Индексы Сущность и виды индексов Индекс представляет собой относительный показатель, характеризующий изменение какого-либо показателя в данном периоде по сравнению с предшествующим. Показатель, по которому находится изменение, называется индексируемым. Индексируемый показатель может быть количественным и качественным. В статистике количественный показатель, независимо от его конкретного содержания называется физическим объемом и обозначается как q. Все остальные показатели называются качественными, т.е. характеризующими единицу совокупности по какому-то признаку (цена - p, себестоимость изделия – s). Индексируемый показатель может относиться к одной единице, в этом случае рассчитывается индивидуальный индекс (например, индекс цены нарезного батона). Индексируемый показатель может относиться к разнородным единицам совокупности, в этом случае рассчитывается общий индекс (например, индекс цены хлебобулочных изделий).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 943; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.76.163 (0.009 с.) |

 ,
,
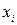 - варианта;
- варианта;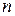 - число единиц совокупности.
- число единиц совокупности.
 - частота.
- частота.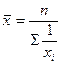 ;
;

 - произведение варианты на частоту.
- произведение варианты на частоту.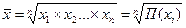


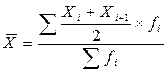 Средний уровень моментного ряда динамики с неравноотстоящими уровнями характеризует средняя хронологическая взвешенная, которая исчисляется по формуле:
Средний уровень моментного ряда динамики с неравноотстоящими уровнями характеризует средняя хронологическая взвешенная, которая исчисляется по формуле: ) - наиболее часто встречающееся значение признака в совокупности. В дискретном ряду мода определяется по наибольшей частоте. Для интервального ряда с равными интервалами мода определяется по формуле:
) - наиболее часто встречающееся значение признака в совокупности. В дискретном ряду мода определяется по наибольшей частоте. Для интервального ряда с равными интервалами мода определяется по формуле: ,
,
 - нижнее значение модального интервала (имеющего наибольшую частоту);
- нижнее значение модального интервала (имеющего наибольшую частоту); - ширина (шаг) интервала;
- ширина (шаг) интервала;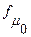 - частота модального интервала;
- частота модального интервала; и
и 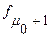 - соответственно: частота интервала, предшествующего (последующего) модальному.
- соответственно: частота интервала, предшествующего (последующего) модальному. ) - середина ранжированного ряда, т.е. величина признака, делящая ряд на две равные части. Для дискретного с нечетным числом уровней медианой будет варианта, находящаяся в середине ряда:
) - середина ранжированного ряда, т.е. величина признака, делящая ряд на две равные части. Для дискретного с нечетным числом уровней медианой будет варианта, находящаяся в середине ряда: ,
,
 – номер медианы.
– номер медианы.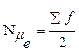 .
.
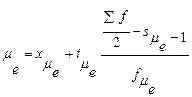 ,
,
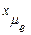 - нижняя граница медианного интервала;
- нижняя граница медианного интервала; -его величина;
-его величина;  - его частота;
- его частота; -сумма накопленных частот в интервалах, предшествующих медианному;
-сумма накопленных частот в интервалах, предшествующих медианному; -сумма частот ряда.
-сумма частот ряда.


 .
. ,
,
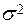 - дисперсия изучаемого признака в изучаемой совокупности. Дисперсия
- дисперсия изучаемого признака в изучаемой совокупности. Дисперсия 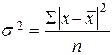 ,
,

 %,
%,




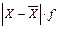


 ;
;
 ,
,

 %
%
 ;
;
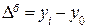 ;
;



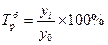


 ;
;
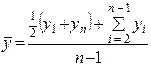 ;
;

 ;
;





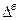




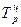


 ,%
,%

 ,
, 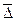 .
.


