
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к выполнению задач и по теме 2 «Статистическое наблюдение» (Выборочное наблюдение)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
После уяснения сущности выборочного наблюдения, понятий генеральной и выборочной совокупностей необходимо понять, что каждая из них характеризуется рядом показателей: средней Выборочные характеристики Разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности.
Выборочная средняя и выборочная доля являются случайными величинами, ошибки выборки также случайны и могут принимать различные значения. Поэтому определяют среднюю из возможных ошибок. При повторном отборе: · для средней:
где,
для доли:
При бесповторном оборе: · для средней
· для доли:
Возможные пределы отклонения выборочной доли и выборочной средней от доли и средней генеральной совокупности носят названия предельных ошибок выборки Предельная ошибка выборки · при определении доли:
· при определении средней:
Величина коэффициента t зависит от вероятности, с которой гарантируется точность расчетов.
Границы искомых показателей в генеральной совокупности определяются так: · для средней
то есть · для доли
то есть Формулы для расчета объема выборки: а) при повторном отборе: · для средней
б) при бесповторном отборе: · для средней:
· для доли:
Задача 1 В городе 100000 семей. Методом случайного бесповторного отбора было обследовано 10000 семей. В результате обследования установлено, что 2000 семей являются владельцами ценных бумаг. С вероятностью 0,954 определите пределы, в которых будет находится доля семей в городе, имеющих ценные бумаги.
Задача 2 Для установления среднего размера краткосрочного кредита в банках города была проведена 5%-ная типическая выборка с пропорциональным отбором внутри типических групп. В результате выборки получены следующие данные:
Задача 3 Для изучения опыта предпринимательской деятельности проведено выборочное обследование предпринимателей региона по стажу работы. Результаты обследования представлены в виде статистического ряда распределения:
По данным выборочного обследования определите: 1. Средний стаж работы предпринимателей; 2. Дисперсию и среднее квадратическое отклонение стажа; 3. Коэффициент вариации; 4. С вероятностью 0,954 возможные пределы в которых ожидается средний стаж работы предпринимателей региона; 5. С вероятностью 0,683 возможные пределы в которых находится доля предпринимателей с опытом работы от 4 до 10 лет. Задача 4 Для изучения размера земельных участков крестьянских хозяйств проведена 1 %-ая выборка по методу типического пропорционального отбора с механическим отбором хозяйств в каждом районе, в результате которой получены следующие данные:
1. Определите с вероятностью до 0,954 возможные пределы среднего размера земельного участка исследуемых районов. 2. Сделайте выводы. Задача 5 Для определения среднего размера вклада в банке и было проведено выборочное обследование 10000 счетов (выборка 10%-ная, механическая). В результате выборки установлено, что средний размер вклада составляет 2000 тыс. руб. при среднем квадратическом отклонении 80 тыс. руб. С вероятностью 0,954 определите границы, в которых будет находиться средний размер вклада в банке. Задача 6 В целях изучения норм расходования дефицитного сырья на изготовление продукции «А» проведена 2%-ная механическая выборка, в результате которой получено следующее распределение:
По данным обследования определите: 1. Средний расход сырья на продукцию «А» 2. Дисперсию, среднее квадратическое отклонение и коэффициент вариации С вероятностью 0,954 предельную ошибку выборочной средней и возможные пределы, в которых ожидается расход сырья для всей изготовленной продукции.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

 , дисперсией
, дисперсией  удельным весом единиц, обладающих данным признаком
удельным весом единиц, обладающих данным признаком 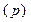 , и не обладающих данным признаком
, и не обладающих данным признаком  ,
,  – численность генеральной совокупности,
– численность генеральной совокупности,  - численность выборочной совокупности.
- численность выборочной совокупности. не совсем точно воспроизводят характеристики генеральной совокупности
не совсем точно воспроизводят характеристики генеральной совокупности  . Расхождения между ними обычно называют ошибками выборочного наблюдения или ошибками репрезентативности.
. Расхождения между ними обычно называют ошибками выборочного наблюдения или ошибками репрезентативности.

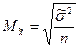
 - средняя ошибка выборки;
- средняя ошибка выборки; - численность единиц выборочной совокупности;
- численность единиц выборочной совокупности; - дисперсия варьирующего признака;
- дисперсия варьирующего признака;
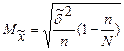
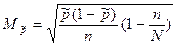
 .
.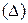 определяется следующим образом:
определяется следующим образом:

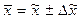
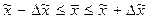

 .
.






