
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показатели размера и интенсивности вариацииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Средняя величина, давая обобщающую характеристику вариационного ряда, не показывает, как располагаются около нее варианты признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. А от размера и распределения отклонений вариант зависят типичность и надежность средних характеристик Следовательно, при характеристике вариационных рядов средние должны быть дополнены показателями вариации, измеряющими отклонения признаков от средней. Вариация - различие значений признака у отдельных единиц совокупности в один и тот же период или момент времени. Вариация вызвана воздействием каких-либо факторов на социально-экономические явления или процессы, причем характер этого воздействия определяет характер колеблемости, изменчивости признака. Поэтому анализ показателей вариации позволяет оценить влияние факторов и условий на изменчивость признаков. Вариация прибыли и рентабельности предприятий обусловлена широким кругом внешних и внутренних факторов. Анализируя вариацию, мы можем определить доминирующие факторы. Например, на предприятиях с минимальной рентабельностью – узкие места, на предприятиях с максимальной рентабельностью – изучение опыта. Статистический анализ вариации включает: 1) построение вариационного ряда 2) графическое изображение ряда 3) расчет показателей центра распределения и структурных характеристик вариационного ряда 4) расчет показателей размера и интенсивности вариации 5) оценка вариационного ряда на асимметрию и эксцесс.
Абсолютные показатели вариации Наиболее простой характеристикой вариации является размах вариации, исчисляемый разностью между наибольшим и наименьшим значениями варьирующего признака: R = xmax–xmin. Этот показатель дает самое общее представление о колеблемости признака, его значение определяется только двумя крайними значениями, тогда как колеблемость признака в целом складывается из всех значений совокупности. Размах вариации предназначен для измерения колеблемости признаков в совокупностях с небольшой численностью единиц. Для характеристики вариации необходимо знать не только размах значений признака, но и обобщенные (суммарные) отклонения всех значений признака от какого-то типичного для изучаемой совокупности значения. В качестве такового обычно используется средняя арифметическая. Характеристика вариации признака на основе отклонений его значений от средней может быть дана с помощью среднего линейного отклонения, рассчитываемого на основе абсолютных отклонений вариантов от их средней: l Первая формула применяется для несистематизированных данных, вторая – в вариационных рядах. Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней арифметической: простая дисперсия s2 взвешенная дисперсия s2 Корень квадратный из дисперсии представляет собой среднее квадратическое отклонение: s = Размах вариации, среднее квадратическое отклонение, среднее линейное отклонение измеряет абсолютную меру колеблемости признака и выражается в тех же единицах измерения, что и варианты. Дисперсия единицы измерения не имеет. В зарубежной статистической практике среднее квадратическое отклонение называется стандартным отклонением и применяется в различных стандартах. Еще одним показателем силы вариации, характеризующим ее не по всей совокупности, а лишь в центральной части, служит среднее квартильное расстояние, т.е. средняя величина разности между квартилями:
Относительные показатели вариации Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более для разных признаков необходимы относительные показатели вариации. Они вычисляются как отношения абсолютных показателей силы вариации, рассмотренных ранее, к средней арифметической величине признака. Т.о. получаем следующие относительные показатели вариации: 1. относительный размах вариации (коэффициент осцилляции) 2. относительное отклонение по модулю (коэффициент вариации по среднему линейному отклонению, линейный коэффициент вариации) 3. коэффициент вариации (коэффициент вариации по среднему квадратическому отклонению) Коэффициент вариации по среднему квадратическому отклонению в статистике играет важную роль. Из теории математической статистики известно, что можно говорить об однородности изучаемой совокупности, если выдерживается неравенство
Поэтому коэффициент вариации по среднему квадратическому отклонению является критерием типичности средней и однородности совокупности. 4. относительное квартильное расстояние
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1013; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.207.11 (0.009 с.) |

 , l
, l  .
. ;
; .
. ; s =
; s =  .
.
 ,
, ,
,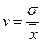 .
.
 .
.


