Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние показатели динамического рядаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Средние величины могут рассчитываться для каждого из рассмотренных выше статистических показателей динамики. 1) Речь идёт о среднем уровне ряда, который характеризует статическую величину абсолютных уровней. 2) Средней абсолютный прирост (∆)представляет собой обобщённую статистическую характеристику индивидуальных (цепных) абсолютных приростов 3) Средний темп роста является обобщающей характеристикой индивидуальных (цепных) темпов роста ряда динамики или накопленного изменения уровня явления за продолжительный период времени. Средний темп роста может быть рассчитан с использованием различных формул: а) как средняя геометрическая из цепных темпов роста (в коэффициентах) Средний темп роста имеет смысл рассчитываться только в тех случаях, кода на протяжении всех лет происходит лишь непрерывный рост, лишь непрерывное сокращение. 4) Средние темпы роста (снижения) рассчитываются на основе средних темпов роста ряда с возрастающими (убывающими) уровнями путём высчитывания их средних 1 или 100 % Как и при расчёте среднего темпа роста, средние темпы прироста (снижения) рассчитываются по рядам, имеющим одно направление развития, и будут в этом отношении качественно однородными. В тех случаях, когда целесообразно определить средний темп динамики на основе резко колеблющихся уровней рядов динамики. Расчёты правильнее производить на основе сравнения средних уровней за определенные временные отрезки (например, пятилетние периоды).
Для получения обобщающих показателей динамики социально -- экономических явлений определяются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста и пр. Средний уровень ряда динамики характеризует типическую величину абсолютных уровней. В интервальных рядах динамики средний уровень у определяется делением суммы уровней В моментном ряду динамики с равноотстоящими датами времени средний уровень определяется по формуле: В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле:
Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. Для определения среднего абсолютного прироста Средний абсолютный прирост может определяться по абсолютным уровням ряда динамики. Для этого определяется разность между конечным Основываясь на взаимосвязи между цепными и базисными абсолютными приростами, показатель среднего абсолютного прироста можно определить по формуле:
Средний темп роста – обобщающая характеристика индивидуальных темпов роста ряда динамики. Для определения среднего темпа роста где Тр1, Тр2,..., Трn -- индивидуальные (цепные) темпы роста (в коэффициентах), n -- число индивидуальных темпов роста. Средний темп роста можно определить и по абсолютным уровням ряда динамики по формуле: На основе взаимосвязи между цепными и базисными темпами роста средний темп роста можно определить по формуле: Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста. При наличии данных о средних темпах роста для получения средних темпов прироста используется зависимость, выраженная формулой:
Вопрос 22.
Виды средних показателей.
Средняя величина – это обобщающий показатель, характеризующий обобщенное значение признака, связи признаков, их динамики и структуры в совокупности массовых явлений. Так, средними в широком смысле слова являются такие показатели, как доля мужчин в общем числе жителей страны (ведь эта доля разная в разных регионах), плотность населения, коэффициент смертности, ожидаемая продолжительность жизни родившихся в данном году и др. В средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. Средние величины делятся на два больших класса: степенные средние, структурные средние. К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая. В качестве структурных средних рассматриваются мода и медиана. Средняя арифметическая величина – это такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – это среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности. Например, средняя зарплата работников предприятия – это такая сумма денег, которая приходилась бы на каждого работника, если бы весь фонд оплаты труда был распределен между работниками поровну.
По данной формуле вычисляются средние величины первичных (объемных) признаков, если известны индивидуальные значения признака. Если изучаемая совокупность велика, исходная информация чаще представляет собой ряд распределения или группировку, например:
Распределение футбольных матчей высшей лиги по числу забитых за матч обеими командами мячей Среднее число мячей, забитых за одну игру, должно представлять собой результат равномерного распределения общего числа забитых мячей по всем 178 матчам. Общее число забитых мячей, исходя из исходной информации в таблице можно получить как сумму произведений значений признака в каждой группе Xi на число игр с таким количеством забитых мячей Fi (частоты). Получим формулу:
Такую формулу средней арифметической величины называют взвешенной арифметической средней. Простая и взвешенная средние величины различаются и по своей роли в решении различных задач статистического анализа. Рассмотрим, например, среднюю величину урожайности картофеля в группе хозяйств. Если эта средняя величина при решении поставленной задачи входит в систему показателей площади посадки, валового сбора, себестоимости, суммы затрат и других характеристик производства, то следует применять взвешенную среднюю, так как произведение невзвешенной средней на общую сумму площадей не даст суммы валового сбора. Если же нас интересуют такие задачи, как измерение вариации урожайности между хозяйствами или связь урожайности с дозой органических удобрений, то следует применять простую среднюю величину урожайности, полностью абстрагируясь от размеров площадей посадки. Иначе на полученный результат повлияют различия площадей, совершенно не касающиеся этого признака.
Степенные средние. Средняя арифметическая величина является частным случаем, который называется степенной средней. Степенная средняя степени k есть корень k-й степени из частного от деления суммы индивидуальных значений признака в k-й степени на число индивидуальных значений. Последовательно придавая k дискретное значение 0, 1, 2, 3, … и т.д. получим различные виды средних. Если k=-1 степенные средние приобретают вид средней гармонической. Пример: В течение рабочей смены 3 рабочих изготовляли детали. 1й рабочий затрачивая на изготовление 1 детали – 6 мин., 2й– 8 мин., 3й– 7,5 мин. Определить средние затраты времени на изготовление 1 детали. Среднюю арифметическую взвешенную нельзя использовать для расчета, так как каждый из рабочих изготавливал за смену разное количество деталей. В числителе формулы отражается количество человеко-силы, а в знаменателе условное количество деталей, изготавливаемых за смену.
Пример: Продавец в течении нескольких дней продавал на рынке морковь. В первые 4 дня цена составляла 6 руб./кг, в последние 5 дней цена поднялась до 7 руб., а оставшаяся морковь была продана за 4,50 руб./кг. Поскольку данные о товарообороте отсутствуют, то для решения задачи применяется средняя гармоническая взвешенная: При этом число дней продаж моркови по различным ценам рассматривается как показатель условного товарооборота. Средняя гармоническая применяется в тех случаях, когда частоты ряда выражены в неявном виде.
Если величина k=0, то степенная средняя приобретает вид средней геометрической. Средняя геометрическая применяется в тех случаях, когда отдельные варианты ряда резко отличаются от остальных. Наиболее часто формулу средней геометрической используют для определения средних валютных курсов, эффективности валютных курсов, реальной эффективности валютных курсов (международная финансовая статистика). Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину.
Если k=1 степенная средняя принимает вид средней арифметической, взвешенной и невзвешенной. Если k=2, средняя квадрата. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной.
Например, имеются три участка земельной площади со сторонами квадрата: х1= 100м, х2= 200 м, х3= 300м.
Результаты статистического исследования зависят от того, насколько верно избран вид средней. Расчет средних, выполненных на основе одних и тех же данных разными способами дает различные результаты.
Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен.
В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.
где XMe – нижняя граница медианного интервала; hMe – его величина; (Sum m)/2 – половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении); SMe-1 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; mMe – число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении).
Показатели вариации
Конкретные условия, в которых находится каждый из изучаемых объектов, а также особенности их собственного развития (социальные, экономические и пр.) выражаются соответствующими числовыми уровнями статистических показателей. Таким образом, вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления.
Для измерения вариации в статистике применяют несколько способов.
Наиболее простым является расчет показателя размаха вариации Н как разницы между максимальным (Xmax) и минимальным (Xmin) наблюдаемыми значениями признака:
H=Xmax - Xmin.
Однако размах вариации показывает лишь крайние значения признака. Повторяемость промежуточных значений здесь не учитывается.
Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение Л как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
Показатель среднего линейного отклонения нашел широкое применение на практике. С его помощью анализируются, например, состав работающих, ритмичность производства, равномерность поставок материалов, разрабатываются системы материального стимулирования. Но, к сожалению, этот показатель усложняет расчеты вероятностного типа, затрудняет применение методов математической статистики. Поэтому в статистических научных исследованиях для измерения вариации чаще всего применяют показатель дисперсии.
Дисперсия признака (s2) определяется на основе квадратической степенной средней:
Показатель s, равный Показатели относительного рассеивания. Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.
В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.
Вопрос 23.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 795; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.011 с.) |

 на их число n:
на их число n: 

 , где
, где  – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени
– уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени 
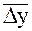 сумма цепных абсолютных приростов
сумма цепных абсолютных приростов  делится на их число n:
делится на их число n: 
 и базисным
и базисным  уровнями изучаемого периода, которая делится на m – 1субпериодов:
уровнями изучаемого периода, которая делится на m – 1субпериодов: 

 применяется формула:
применяется формула: 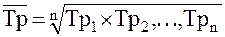


 (при выражении среднего темпа роста в коэффициентах)
(при выражении среднего темпа роста в коэффициентах) Х – средняя величина, n – численность совокупности.
Х – средняя величина, n – численность совокупности.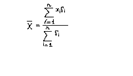




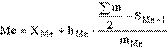
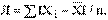

 , называется средним квадратическим отклонением.
, называется средним квадратическим отклонением.