
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние показатели в рядах динамики и методы их исчисленияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Каждый ряд динамики можно рассматривать как некую совокупность m меняющихся во времени показателей, которые можно обобщать в виде средних величин. Для обобщения данных по рядам динамики рассчитываются: средний уровень ряда; средний абсолютный прирост; средний темп роста и прироста. Средний уровень ряда динамики (у¯) рассчитывается по средней хронологической. Средней хронологической называется средняя, исчисленная из значений, изменяющихся во времени. Такие средние обобщают хронологическую вариацию. В хронологической средней отражается совокупность тех условий, в которых развивалось изучаемое явление в данном промежутке времени. Средний уровень ряда определяется по-разному для моментных и интервальных рядов. • Для интервальных равноотстоящих рядов средней уровень находится по формуле
где n - число уровней или длина ряда. • Для интервальных неравноотстоящих рядов средний уровень находится по формуле взвешенной средней арифметической:
где ti — продолжительность интервалов времени между уровнями (число периодов времени, при которых значение уровня не изменяется).
Пример. В таблице 9.7. приведен интервальный ряд динамики с равноотстоящими уровнями. По этим данным можно рассчитать среднегодовой уровень числа проданных квартир за 2000-2004 гг. Он будет равен 347 тыс.ед. (у¯ = 1735/5), то есть в среднем ежегодно число проданных квартир в регионе за 2000-2004 гг. составило полученное значение. • Средний уровень моментного равноотстоящего ряда динамики находится по формуле средней хронологической простой:
• Средний уровень моментных рядов динамики с неравноотстоящими уровнями определяется по формуле средней хронологической взвешенной:
где t - продолжительность интервала времени между соседними уровнями. Пример. Покажем расчет среднего уровня моментного ряда динамики с равноотстоящими уровнями по данным о численности работников фирмы на 1-е число каждого месяца 2004 г. (чел.): 1/I 1/II 1/III 1/IV 347 350 349 351 Среднемесячная численность работников фирмы за 1 квартал (по формуле 9.16) составит:
Пример. Известна списочная численность рабочих организаций на некоторые даты 2004 г. (чел.)- Ряд динамики имеет не равноотстоящие уровни во времени:
1/I 1/III 1/VI 1/IX 1/I-1995 530 570 520 430 550
Среднегодовая численность работников за 1994 г. (по формуле 9.17) составит:
Обобщающим показателем абсолютной скорости изменения явления во времени является средний абсолютный прирост за весь период, ограничивающий ряд динамики. Скоростью в данном случае будем называть прирост (уменьшение) в единицу времени. Для его определения используется формула средней арифметической простой:
Подставив в числитель выражение для цепных абсолютных приростов, получим более удобную форму записи для среднего абсолютного прироста:
где уn и y1 - соответственно конечный и начальный уровни ряда динамики. Пример. По данным таблицы 9.7 определим средний абсолютный прирост числа проданных квартир за период 2000-2004 гг. Он будет равен 1,0 тыс.ед. [(112-108): 4]. Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста. Он показывает, сколько в среднем процентов последующий уровень составляет от предыдущего в течение всего периода наблюдения. Средний темп (коэффициент) роста рассчитывается по формуле средней геометрической из цепных коэффициентов роста:
Выразив цепные коэффициенты (темпы) роста через соответствующие уровни ряда, получим:
Пример. По данным таблицы 9.7 рассчитаем средний темп роста числа проданных квартир за период 2000-2004 гг. по формуле 9.21:
или по формуле: Когда приходится производить расчет средних темпов роста по периодам различной продолжительности (не равноотстоящие уровни), то используют среднюю геометрическую, взвешенную по продолжительности периодов. Формула средней геометрической взвешенной будет иметь вид:
где t - интервал времени, в течение которого сохраняется данный темп роста. Средний темп прироста не может быть определен непосредственно на основании последовательных темпов прироста или показателей среднего абсолютного прироста. Для его вычисления необходимо сначала найти средний темп роста, а затем его уменьшить на единицу или на 100%:
Пример. По данным таблицы 9.7 был рассчитан средний темп роста числа проданных квартир за 2000-2004 гг. равный 100,9%, отсюда средний темп прироста будет равен:
9.5. Методы анализа основной тенденции (тренда) в рядах динамики Важной задачей статистики при анализе рядов динамики является определение основной тенденции развития, присущей тому или иному ряду динамики. Под основной тенденцией развития ряда динамики понимают изменение, определяющее общее направление развития. Это — систематическая составляющая долговременного действия. В некоторых случаях общая тенденция ясно прослеживается в динамике рассматриваемого показателя, в других случаях она может не просматриваться из-за ощутимых случайных колебаний. Например, в отдельные моменты времени сильные колебания розничных цен могут заслонить наличие тенденции к росту или снижению этого показателя. Поэтому для выявления основной тенденции развития в статистике применяются 2 группы методов: • сглаживание или механическое выравнивание отдельных уровней ряда динамики с использованием фактических значений соседних уровней; • выравнивание с применением кривой, проведенной между конкретными уровнями таким образом, чтобы она отражала тенденцию, присущую ряду и одновременно освободила его от незначительных колебаний. Рассмотрим методы каждой группы. Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни. Например, ряд недельных данных можно преобразовать в ряд помесячной динамики, ряд квартальных данных заменить годовыми уровнями. Уровни нового ряда могут быть получены путем суммирования уровней исходного ряда, либо могут представлять средние уровни. Распространенным приемом при выявлении тенденции развития является сглаживание ряда динамики. Суть различных приемов сглаживания сводится к замене фактических уровней ряда расчетными уровнями, которые в меньшей степени подвержены колебаниям. Это способствует более четкому проявлению тенденции развития. Метод простой скользящей средней. Сглаживание ряда динамики с помощью скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем средний уровень из такого же числа уровней, начиная со второго, далее - начиная с третьего и т.д. Таким образом, при расчете средних уровней они как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень вначале и добавляя один следующий. Отсюда название - скользящая средняя. Каждое звено скользящей средней - это средний уровень за соответствующий период, который относится к середине выбранного периода, если число уровней ряда динамики нечетное. Нахождение скользящей средней по четному числу членов рядов динамики несколько сложнее, так как средняя может быть отнесена только к середине между двумя датами, находящимся в середине интервала сглаживания. Например, средняя, найденная для четырех уровней, относится к середине между вторым и третьим, третьим и четвертым уровнями и так далее. Чтобы ликвидировать такой сдвиг, применяют так называемый способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенной дате. При центрировании необходимо находить скользящие суммы, скользящие средние нецентрированные по этим, суммам и средние из двух смежных нецентрированных скользящих средних. Пример. Покажем расчет скользящей средней за 3 и 4 месяца по данным, представленным в таблице 9.6. Таблица 9.6.
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 695; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

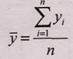 (9.14.)
(9.14.) (9.15.)
(9.15.) (9.16.)
(9.16.) (9.17.)
(9.17.)

 (9.18.)
(9.18.) (9.19.)
(9.19.) (9.20.)
(9.20.) (9.21.)
(9.21.)

 (9.22.)
(9.22.) (9.23.)
(9.23.)



