
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структура валового внутреннего продукта РФ в 1 квартале 2003 Г.Содержание книги
Поиск на нашем сайте
Рассчитанные в последней графе данной таблицы проценты представляют собой относительные показатели структуры (в данном случае - удельные веса). Сумма всех удельных весов всегда должна быть строго равна 100% или 1. Относительный показатель координации представляет собой отношение одной части совокупности к другой части этой же совокупности:
При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают, во сколько раз данная часть больше базисной или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда - на 100, 1000 и т.д. единиц) базисной структурной части. Так, на основе данных приведенной выше таблицы 3.2 мы можем вычислить, что на каждый рубль произведенных товаров приходится 1,8 руб. произведенных услуг Относительный показатель интенсивности характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:
Данный показатель получают сопоставлением уровней двух взаимосвязанных в своем развитии явлений. Поэтому, наиболее часто он представляет собой именованную величину, но может быть выражен и в процентах, промилле, продецимилле. Обычно относительный показатель интенсивности рассчитывается в тех случаях, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения. Так, например, для определения уровня обеспеченности населения легковыми автомобилями рассчитывается число автомашин, приходящихся на 100 семей, для определения плотности населения рассчитывается число людей, приходящихся на 1 кв.км. Так, по данным социальной статистики на конец 2003 г. общая численность безработных в РФ составляла 6,1 млн. чел., а экономически активное население - 70,9 млн. чел. Отсюда следует, что уровень безработицы составлял Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства или региона. Так как объемные показатели производства продукции по своей природе являются интервальными, а показатель численности населения - моментным, в расчетах используют среднюю за период численность населения (предположим, среднегодовую). Например, рассматривая лишь абсолютный размер ВВП России в 1 квартале 2003 года (2893 млрд. руб.), трудно оценить или "почувствовать" эту величину. Для того, чтобы на основе данной цифры сделать вывод об уровне развития экономики, необходимо сопоставить ее со среднеквартальной численностью населения страны (145,2 млн.чел), которая в простейшем случае рассчитывается как полусумма численности населения на начало и на конец квартала. В результате квартальный размер ВВП на душу населения составит 19,9 тыс. руб. Относительный показатель сравнения представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.):
Для выражения данного показателя могут использоваться как коэффициенты, так и проценты. Например, согласно официальным статистическим данным, инвестиции в основной капитал в РФ в 2002 г. за счет средств федерального бюджета составили 81,6 млрд. руб., бюджетов субъектов Федерации и местных бюджетов - 184,5 млрд. руб., средств предприятий - 653,1 млрд. руб. Таким образом можно сделать вывод, что инвестиции за счет средств предприятий в 8 раз превышали инвестиции из средств федерального бюджета и в 3,5 раза превышали инвестиции из бюджетов субъектов Федерации и местных бюджетов.
Средние показатели
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности. Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимым инструментом анализа явлений и процессов в экономике. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу. Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам. Типичность средней непосредственным образом связана с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности. Так если мы рассчитаем средний курс по акциям всех предприятий, реализуемых в данный день на данной бирже, то получим фиктивную среднюю. Это будет объясняться тем, что используемая для расчета совокупность является крайне неоднородной. В этом и подобных случаях метод средних используется в сочетании с методом группировок: если совокупность неоднородна - общие средние должны быть заменены или дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам. Категорию средней можно раскрыть через понятие ее определяющего свойства. Согласно этому понятию средняя, являясь обобщающей характеристикой всей совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности. Эту величину можно представить в виде функции: f(x1,x2,...,xn) (5.1.) Так как данная величина, в большинстве случаев, отражает реальную экономическую категорию, понятие определяющего свойства средней иногда заменяют понятием определяющего показателя. Если в приведенной выше функции все величины x1,x2,…,xn заменить их средней величиной х, то значение этой функции должно остаться прежним: f(x1,x2,..,xn)=f(x¯,x¯,…,x¯)(5.2.) Исходя из данного равенства и определяется средняя. На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:
Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:
Числитель исходного соотношения средней представляет собой определяющий показатель. Для средней заработной платы таким определяющим показателем является фонд заработной платы. Независимо от того, какой первичной информацией мы располагаем - известен ли нам общий фонд заработной платы или заработная плата и численность работников, занятых на отдельных должностях, или какие-либо другие исходные данные - в любом случае среднюю заработную плату можно получить только через данное исходное соотношение средней. Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней. Если, например, требуется рассчитать средний размер вклада в банке, то исходное соотношение будет следующим:
Если же необходимо определить среднюю процентную ставку по кредитам, выданным на один и тот же срок, то потребуется следующее исходное соотношение:
Однако от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины: • средняя арифметическая, • средняя гармоническая, • средняя геометрическая, • средняя квадратическая, кубическая и т.д. Перечисленные средние объединяются в общей формуле средней степенной (при различной величине k):
где: х j - i-ый вариант осредняемого признака (i=l,n) f, - вес i-ro варианта. Помимо степенных средних в экономической практике также используются средние структурные, среди которых наиболее распространены мода и медиана. При осреднении уровней динамических рядов применяются различные виды средней хронологической. Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных, может быть простой или взвешенной. Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным. Предположим, шесть торговых предприятий фирмы имеют следующий объем товарооборота за месяц:
Для того, чтобы определить средний месячный товарооборот в расчете на одно предприятие, необходимо воспользоваться следующим исходным соотношением:
Используя приведенные в предыдущем параграфе условные обозначения, запишем формулу данной средней:
С учетом имеющихся данных получим:
В данном случае мы использовали формулу средней арифметической простой (невзвешенной). Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными. Рассмотрим следующий условный пример: Таблица 5.3.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.37.242 (0.007 с.) |



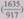 и 0,4 руб. чистых налогов на продукты
и 0,4 руб. чистых налогов на продукты  .
.
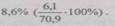
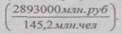







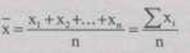 (5.3.)
(5.3.)



