Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные характеристики корпоративных ценных бумаг
Система нормальных линейных уравнений имеет вид:
Для определения параметров линейного уравнения регрессии составим расчетную таблицу: Таблица 8. Расчетная таблица для определения параметров Уравнения регрессии выручки от реализации корпоративных ценных бумаг
Система уравнений примет следующий вид:
Таким образом:
Собственно-корреляционные параметрические методы изучения связи
Измерение тесноты (силы) и направления связи является важной задачей изучения количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака и одного (при изучении парных зависимостей) или нескольких (множественных зависимостей) факторных признаков. Линейный коэффициент корреляции (К. Пирсона) характеризует тесноту и правление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. В теории разработаны и на практике применяются различные модификации формулы расчета данного коэффициента:
Производя расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции можно вычислить по формуле:
Между линейным коэффициентом корреляции и коэффициентом регрессии
где ai - коэффициент регрессии в уравнении связи; ах - среднее квадратическое отклонение соответствующего, статистически существенного, факторного признака. Линейный коэффициент корреляции изменяется в пределах от -1 до 1: [-1≤r≤1].
Таблица 8.6. Оценка линейного коэффициента корреляции
Пример. На основе выборочных данных о деятельности 6 предприятий одной из отраслей промышленности Российской Федерации оценить тесноту связи между трудоемкостью продукции предприятия (X, чел.-час.) и объемом ее производства (Y, млн. руб.) Таблица 8.7. Расчетная таблица для определения коэффициента корреляции
1. Используя формулу (8.4), получаем:
2. По формуле (8.5) значение коэффициента корреляции составило:
Таким образом, результат по всем формулам одинаков и свидетельствует о сильной обратной зависимости между изучаемыми признаками. В случае наличия линейной или нелинейной зависимости между двумя признаками для измерения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляционное отношение. Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда δ2характеризует отклонения групповых средних результативного показателя от 1бщей средней:
где η - корреляционное отношение; σ2 - общая дисперсия; σ¯2 - средняя из частных (групповых) дисперсий; δ2 - межгрупповая дисперсия (дисперсия групповых средних). Все эти дисперсии есть дисперсии результативного признака. Теоретическое корреляционное отношение определяется по формуле:
где δ2 - дисперсия выровненных значений результативного признака, то есть рассчитанных по уравнению регрессии; σ2 - дисперсия эмпирических (фактических) значений результативного признака; σ2ост - остаточная дисперсия. Корреляционное отношение изменяется в пределах от 0 до 1 (0≤ η ≤1) Для измерения тесноты связи при множественной корреляционной зависимости, то есть при исследовании трех и более признаков одновременно, вычисляется множественный и частные коэффициенты корреляции. Множественный коэффициент корреляции вычисляется при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой факторных признаков. Множественный коэффициент корреляции для двух факторных признаков вычисляется по формуле:
Где ryxi - парные коэффициенты корреляции между признаками.
Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по На основе данных таблицы 8.4 рассчитаем коэффициент множественной корреляции:
Множественный коэффициент корреляции составит:
Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками x1 и x2 при фиксированном значении других (k-2) факторных признаков, то есть когда влияние x3 исключается, то есть оценивается связь между x1 и x2 в «чистом виде». В случае зависимости у от двух факторных признаков x1 и x2 коэффициенты частной корреляции имеют вид:
Где r - парные коэффициенты корреляции между указанными в индексе переменными. В первом случае исключено влияние факторного признака х2, во втором – х1. На основании приведенных выше данных о зависимости трех факторов деятельности предприятий вычислим частные коэффициенты корреляции (табл. 8.4):
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 272; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.72.232 (0.017 с.) |
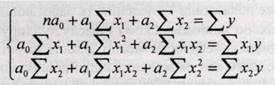
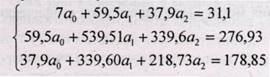
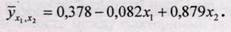
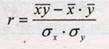
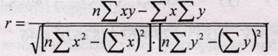 (8.5)
(8.5)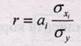 (8.6)
(8.6)

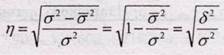 (8.7)
(8.7)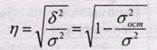 (8.7.)
(8.7.)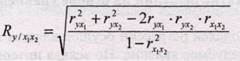 (8.9.)
(8.9.)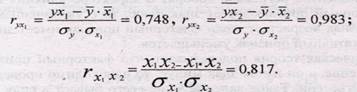

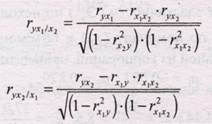 (8.10.)
(8.10.)