
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множественная (многофакторная) регрессияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии:
Построение моделей множественной регрессии включает несколько этапов:
Выбор типа уравнения затрудняется тем, что для любой формы зависимости можно выбрать целый ряд уравнений, которые в определенной степени будут описывать эти связи. Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Важным этапом построения уже выбранного уравнения множественной регрессии является отбор и последующее включение факторных признаков. С одной стороны, чем больше факторных признаков включено в уравнение, тем оно лучше описывает явление. Однако модель размерностью 100 и более факторных признаков сложно реализуема и требует больших затрат машинного времени. Сокращение размерности модели за счет исключения второстепенных, экономически и статистически несущественных факторов способствует простоте и качеству ее реализации. В то же время построение модели регрессии малой размерности может привести к тому, что такая модель будет недостаточно адекватна исследуемым явлениям и процессам. Проблема отбора факторных признаков для построения моделей взаимосвязи может быть решена на основе интуитивно-логических или многомерных математико-статистических методов анализа. Наиболее приемлемым способом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность метода шаговой регрессии заключается в реализации алгоритмов последовательного «включения», «исключения» или «включения-исключения» факторов в уравнение регрессии и последующей проверке их статистической значимости. Алгоритм «включения» заключается в том, что факторы поочередно вводятся в уравнение так называемым «прямым методом». При проверке значимости введенного фактора определяется, на сколько уменьшается сумма квадратов остатков и увеличивается величина множественного коэффициента корреляции (R2). Одновременно используется и алгоритм последовательного «исключения», сущность которого заключается в том, что исключаются факторы, ставшие незначимыми по статистическим критериям. Фактор является незначимым, если его включение в уравнение регрессии только изменяет значения коэффициентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения. Если при включении в модель соответствующего факторного признака величина множественного коэффициента корреляции увеличивается, а коэффициента регрессии не изменяется (или меняется несущественно), то данный признак существенен и его включение в уравнение регрессии необходимо. В противном случае, фактор нецелесообразно включать в модель регрессии. При построении модели регрессии возможна проблема мультиколлинеарности, под которой понимается тесная зависимость между факторными признаками, включенными в модель (rxy > 0,8). Наличие мультиколлинеарности между признаками вызывает: • искажение величины параметров модели, которые имеют тенденцию к завышению, чем осложняется процесс определения наиболее существенных факторных признаков; • изменение смысла экономической интерпретации коэффициентов регрессии. В качестве причин возникновения мультиколлинеарности между признаками можно выделить следующие: • изучаемые факторные признаки являются характеристикой одной и той же стороны изучаемого явления или процесса. Например: показатели объема производимой продукции и среднегодовой стоимости основных фондов одновременно включать в модель не рекомендуется, так как они оба характеризуют размер предприятия; • факторные признаки являются составляющими элементами друг друга. Например: показатели выработки продукции на одного работающего и численность работающих одновременно в модель включать нельзя, так как в основе расчета показателей лежит один и тот же показатель - численность работающих на предприятии. • факторные признаки по экономическому смыслу дублируют друг друга. Устранение мультиколлинеарности может реализовываться через исключение из корреляционной модели одного или нескольких линейно-связанных факторных признаков или преобразование исходных факторных признаков в новые, укрупненные факторы. Вопрос о том, какой из факторов следует отбросить, решается на основании качественного, логического анализа изучаемого явления, а также на основе анализа тесноты связимежду результативным (у) с каждым из сильно коллинеарно связанных факторных признаков. Из дальнейшего анализа целесообразно исключить тот факторный признак, которого с результативным наименьшая. Качество уравнения регрессии зависит от степени достоверности и надежности исходных данных и объема совокупности. Исследователь должен стремиться к увеличению - числа наблюдений, так как большой объем наблюдений является одной из предпосылок построения адекватных статистических моделей. Аналитическая форма связи результативного признака от нескольких факторных чается и называется многофакторным (множественным) уравнением регрессии или моделью связи. Линейное уравнение множественной регрессии имеет вид:
x1,x2,…,xk — факторные признаки; a1,а2,…,аk — параметры модели (коэффициенты регрессии). Параметры уравнения могут быть определены графическим методом или методом наименьших квадратов. Пример. По следующим данным о выручке (у), спросу по номиналу (x1)и объему продаж (х2) корпоративных ценных бумаг определим зависимость между признаками. Таблица 8.4.
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 453; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.198.113 (0.007 с.) |


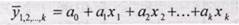
 - теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии;
- теоретические значения результативного признака, полученные в результате подстановки соответствующих значений факторных признаков в уравнение регрессии;


